Aizu_Insertion Sort
原题链接:https://vjudge.net/problem/Aizu-ALDS1_1_A
题目描述
Write a program of the Insertion Sort algorithm which sorts a sequence A in ascending order. The algorithm should be based on the following pseudocode:
for i = 1 to A.length-1
key = A[i]
/* insert A[i] into the sorted sequence A[0,...,j-1] */
j = i - 1
while j >= 0 and A[j] > key
A[j+1] = A[j]
j--
A[j+1] = key
Note that, indices for array elements are based on 0-origin.
To illustrate the algorithms, your program should trace intermediate result for each step.
Input
The first line of the input includes an integer N, the number of elements in the sequence.
In the second line, N elements of the sequence are given separated by a single space.
Output
The output consists of N lines. Please output the intermediate sequence in a line for each step. Elements of the sequence should be separated by single space.
Constraints
1 ≤ N ≤ 100
Sample Input 1
6 5 2 4 6 1 3
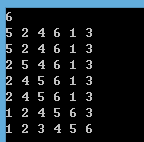
Sample Output 1
5 2 4 6 1 3 2 5 4 6 1 3 2 4 5 6 1 3 2 4 5 6 1 3 1 2 4 5 6 3 1 2 3 4 5 6
Sample Input 2
3 1 2 3
Sample Output 2
1 2 3 1 2 3 1 2 3
讲解
插入排序法
- 将开头元素视作已排序
- 执行下述处理,直至未排序部分消失
- 取出未排序部分的开头元素赋给变量v。
- 在已排序部分,将所有比v大的元素向后移动一个单位。
- 将已取出的元素v插入空位。
举例说明
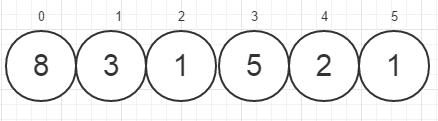
当对数组A = {8,3,1,5,2,1}进行从小到大的插入排序时,流程如下
0.
1.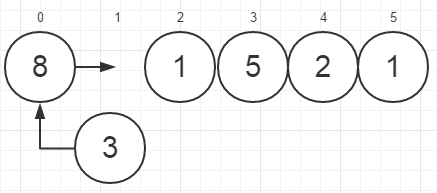
将开头元素A[0](=8)视为已排序,所以我们取出A[1]中的3,将其插入已排序部分的恰当位置。
首先把原先位于A[0]的8移动至A[1],再把3插入A[0]。
2.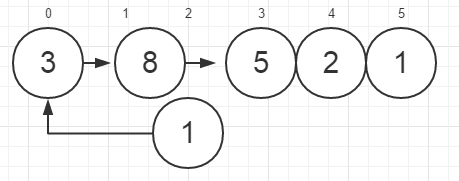
首先将比1大的A[1](=8)和A[0](=3)顺次向后移动一个位置,然后把1插入A[0]。
3.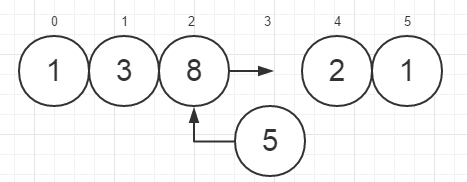
首先将比5大的A[2](=8)向后移动一个位置,然后把5插入A[2]。
4.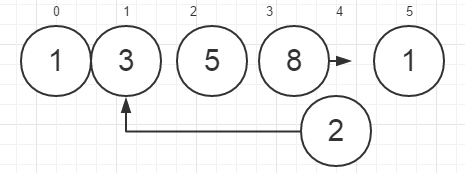
首先将比5大的A[3](=8)向后移动一个位置,然后把2插入A[1]。
5.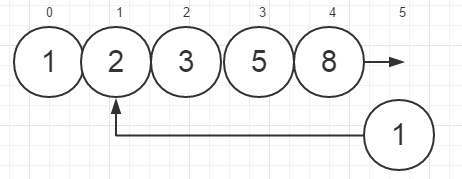
首先将比5大的A[4](=8)向后移动一个位置,然后把1插入A[1]。
6.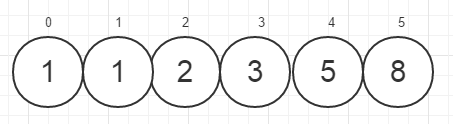
排序完成。
插入排序法所需的主要变量
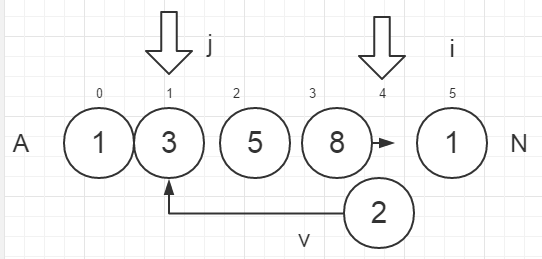
|
A[N] |
长度为N的整型数组 |
|
i |
循环变量,表示未排序部分的开头元素 |
|
v |
临时保存A[i]值的变量 |
|
j |
循环变量,用于在已排序部分寻找v的插入位置 |
外层循环的 i 从1开始自增。在每次循环开始时,将A[i]的值临时保存在变量v中。
接下来是内部循环:从已排序部分找出比v大的元素并让它们顺次后移一个位置。在这里,我们让 j 从 i - 1 开始向前自减,同时将比v大的元素从A[j]移动到A[j+1]。一旦j等于-1或当前A[j]小于等于v则结束循环,并将v插入当前 j+1 的位置。
程序代码及细节
#include<stdio.h> void trace(int A[],int N){ //按顺序输出数组元素 int i; for(i=0;i<N;i++){ if(i>0) printf(" "); //在相邻元素之间输出1个空格 printf("%d",A[i]); } printf("\n"); } void insertionSort(int A[],int N){ //插入排序(数组下标从0开始) int j,i,v; for(i=1;i<N;i++){ v=A[i]; j=i-1; while(j>=0 && A[j]>v){ A[j+1]=A[j]; j--; } A[j+1]=v; trace(A,N); } } int main() { int N,i,j; int A[100]; scanf("%d",&N); for(i=0;i<N;i++) scanf("%d",&A[i]); trace(A,N); insertionSort(A,N); return 0; }
细节关注
- 数组长度是否足够长
- 是否搞错了0起点和1起点的数组下标
- 是否误用了循环变量
- 是否输出了多余的空格或换行
总结
稳定性:在插入排序法中,我们只将比v(取出的值)大的元素向后平移,不相邻的元素不会直接交换位置,因此十分稳定。
时间复杂度:最坏的情况下,每个 i 循环都需要执行 i 次移动,总共需要1 + 2 + ... + N - 1 = (N2 - N)/ 2 次移动,即算法复杂度为 O(N2)。
算法优势:可以快速处理相对有序的数据。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号