ISITDTUCTF2023 babyRSA

chall.py

from Crypto.Util.number import bytes_to_long
from FLAG import flag

p1 = 401327687854144602104262478345650053155149834850813791388612732559616436344229998525081674131271
p2 = 500233813775302774885494989064149819654733094475237733501199023993441312997760959607567274704359
p3 = 969568679903672924738597736880903133415133378800072135853678043226600595571519034043189730269981
e1 = 398119
e2 = 283609
e3 = 272383

c = bytes_to_long(flag)
c = pow(c, e1, p1)
c = pow(c, e2, p2)
c = pow(c, e3, p3)

print(f"{c = }")
# c = 104229015434394780017196823454597012062804737684103834919430099907512793339407667578022877402970

用sage实现的mod_nth_root(python sympy自带的 osoi...)
其中的sqrtn:

这里的z其实就是满足 z ^ e ≡ 1 mod p 这样就可以还原所有的roots

# from Crypto.Util.number import *
from libnum import *
from tqdm import tqdm
from sage.all import pari

p1 = 401327687854144602104262478345650053155149834850813791388612732559616436344229998525081674131271
p2 = 500233813775302774885494989064149819654733094475237733501199023993441312997760959607567274704359
p3 = 969568679903672924738597736880903133415133378800072135853678043226600595571519034043189730269981
e1 = 398119
e2 = 283609
e3 = 272383
c = 104229015434394780017196823454597012062804737684103834919430099907512793339407667578022877402970

def mod_nth_root(x, e, n):
    r, z = pari(f"r = sqrtn(Mod({x}, {n}), {e}, &z); [lift(r), lift(z)]")
    r, z = int(r), int(z)
    roots = [r]
    if z == 0:
        return roots
    t = r
    # while (t := (t*z) % n) != r:
    #     roots.append(t)
    while(True):
        t = (t*z)%n
        if(t==r):
            break
        roots.append(t)
    return roots

for r3 in tqdm(mod_nth_root(c, e3, p3)):
    for r2 in mod_nth_root(r3, e2, p2):
        for flag in mod_nth_root(r2, e1, p1):
            flag = int(flag)
            flag = n2s(flag)
            if b'ISITDTU{' in flag:
                print(flag)

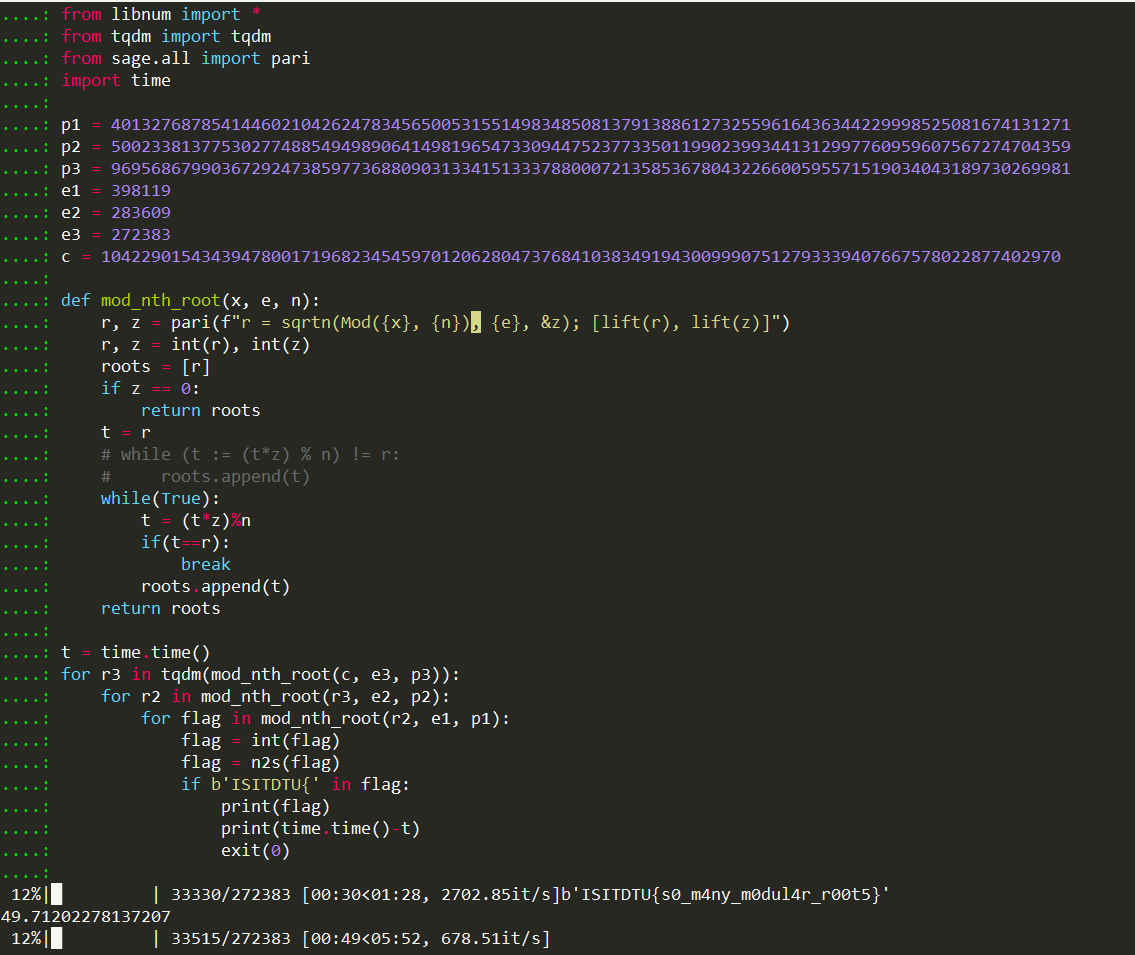
只用了50s就跑出来了。。。
而sympy我挂了一下午还没跑出来。。。