P5091 扩展欧拉定理

【模板】扩展欧拉定理

题目描述

给你三个正整数，\(a,m,b\)，你需要求：\(a^b \bmod m\)

输入格式

一行三个整数，\(a,m,b\)

输出格式

一个整数表示答案

样例 #1

样例输入 #1

2 7 4

样例输出 #1

2

样例 #2

样例输入 #2

998244353 12345 98765472103312450233333333333

样例输出 #2

5333

提示

注意输入格式，\(a,m,b\) 依次代表的是底数、模数和次数

【样例 \(1\) 解释】
\(2^4 \bmod 7 = 2\)

【数据范围】
对于 \(100\%\) 的数据，\(1\le a \le 10^9\)，\(1\le b \le 10^{20000000}，1\le m \le 10^8\)。

原理：a m 不互素的时候就要用扩展欧拉定理

欧拉函数φ(m)的算法

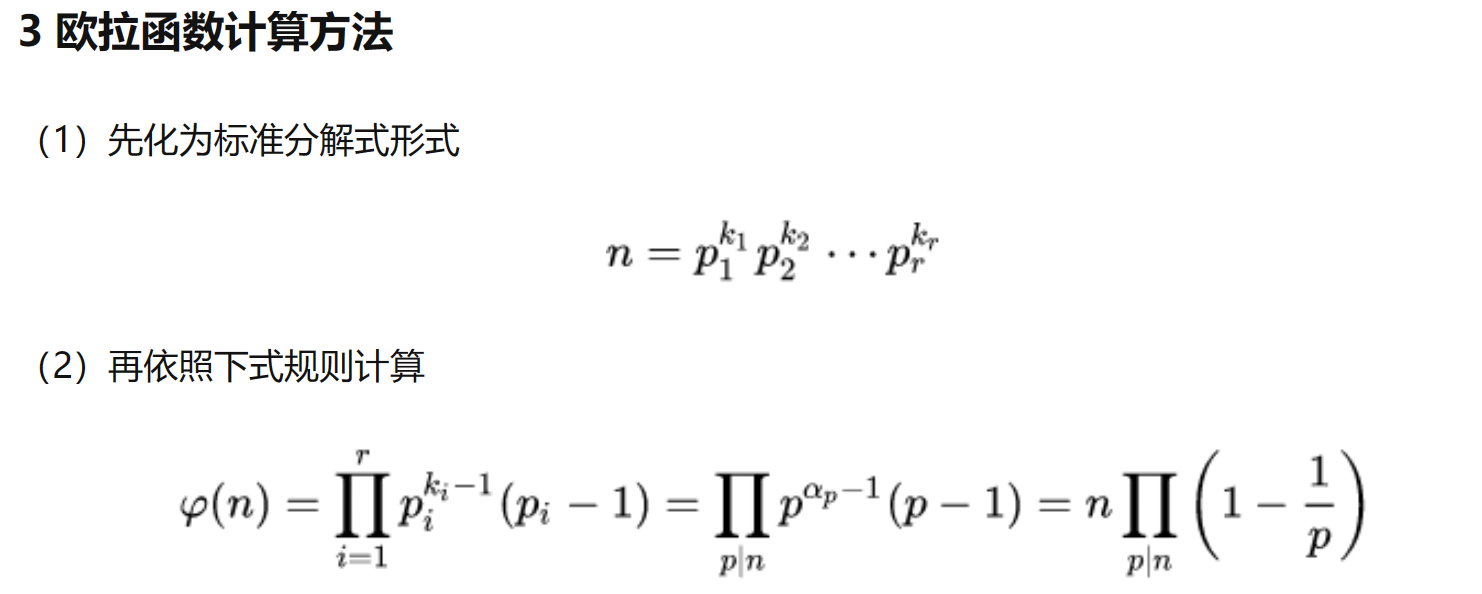
int phi=1;
	for(int i=2;i*i<=mm;i++)
	{
		if(mm%i==0)
		{
			phi*=(i-1);
			mm/=i;
			while(mm%i==0)
			{
				phi*=i;
				mm/=i;
			}
		}	
	} 
	if(mm>1)phi*=(mm-1);//注意最后还有可能剩下质数

由于b很大 所以我们用类似快读的方式读入b 判断大小并取模

最后快速幂计算即可

注意一定要考虑循环结束后的额外判断！

#include<bits/stdc++.h>
using namespace std;
#define int long long
int m;
int qpow(int a,int b) { // a^b mod m
	int tmp=1;
	while(b) {
		if(b&1)tmp=tmp*a%m;
		a=a*a%m;
		b>>=1;
	}
	return tmp;
}
int a,b;
//扩展欧拉定理
signed main() {
	cin>>a>>m;
	a%=m;
	//先算φ(m)
	int mm=m;
	int phi=1;
	for(int i=2; i*i<=mm; i++) {
		if(mm%i==0) {
			phi*=(i-1);
			mm/=i;
			while(mm%i==0) {
				phi*=i;
				mm/=i;
			}
		}
	}
	if(mm>1)phi*=(mm-1);//注意最后还有可能剩下质数
	int bm=0;
	char ch=getchar();//判断 b 与  φ(m) 的大小关系
	int flag=0;
	while(ch<'0'||ch>'9')ch=getchar();
	while(ch>='0'&&ch<='9') {
		bm=(int)10*bm+ch-'0';
		if(bm>=phi)flag=1,bm%=phi;
		ch=getchar();
	}
	if(bm>=phi)flag=1,bm%=phi;
	if(flag)bm+=phi;
	cout<<(qpow(a,bm)%m+m)%m<<"\n";
	return 0;
}