实验作业1

四、实验结论

实验任务1

代码1

// 现代C++标准库、算法库体验
// 本例用到以下内容:
// 1. 字符串string, 动态数组容器类vector、迭代器
// 2. 算法库：反转元素次序、旋转元素
// 3. 函数模板、const引用作为形参
#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
// 模板函数声明
template<typename T>
void output(const T &c);
void test1();
void test2();
void test3();
int main() {
std::cout << "测试1: \n";
test1();
std::cout << "\n测试2: \n";
test2();
std::cout << "\n测试3: \n";
test3();
}
// 输出容器对象c中的元素
template <typename T>
void output(const T &c) {
for(auto &i : c)
std::cout << i << ' ';
std::cout << '\n';
}
// 测试1：组合使用算法库、迭代器、string反转字符串
void test1() {
using namespace std;
string s0{"0123456789"};
cout << "s0 = " << s0 << endl;
string s1(s0);
// 反转s1自身
reverse(s1.begin(), s1.end());
cout << "s1 = " << s1 << endl;
string s2(s0.size(), ' ');
// 将s0反转后结果拷贝到s2, s0自身不变
reverse_copy(s0.begin(), s0.end(), s2.begin());
cout << "s2 = " << s2 << endl;
}
// 测试2：组合使用算法库、迭代器、vector反转动态数组对象vector内数据
void test2() {
using namespace std;
vector<int> v0{2, 0, 4, 9};
cout << "v0: "; output(v0);
vector<int> v1{v0};
reverse(v1.begin(), v1.end());
cout << "v1: "; output(v1);
vector<int> v2{v0};
reverse_copy(v0.begin(), v0.end(), v2.begin());
cout << "v2: "; output(v2);
}
// 测试3：组合使用算法库、迭代器、vector实现元素旋转移位
void test3() {
using namespace std;
vector<int> v0{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
cout << "v0: "; output(v0);
vector<int> v1{v0};
// 将[v1.begin(), v1.end())区间内元素循环左移1位
rotate(v1.begin(), v1.begin()+1, v1.end());
cout << "v1: "; output(v1);
vector<int> v2{v0};
// 将[v1.begin(), v1.end())区间内元素循环左移2位
rotate(v2.begin(), v2.begin()+2, v2.end());
cout << "v2: "; output(v2);
vector<int> v3{v0};
// 将[v1.begin(), v1.end())区间内元素循环右移1位
rotate(v3.begin(), v3.end()-1, v3.end());
cout << "v3: "; output(v3);
vector<int> v4{v0};
// 将[v1.begin(), v1.end())区间内元素循环右移2位
rotate(v4.begin(), v4.end()-2, v4.end());
cout << "v4: "; output(v4);
}

运行截图1

 

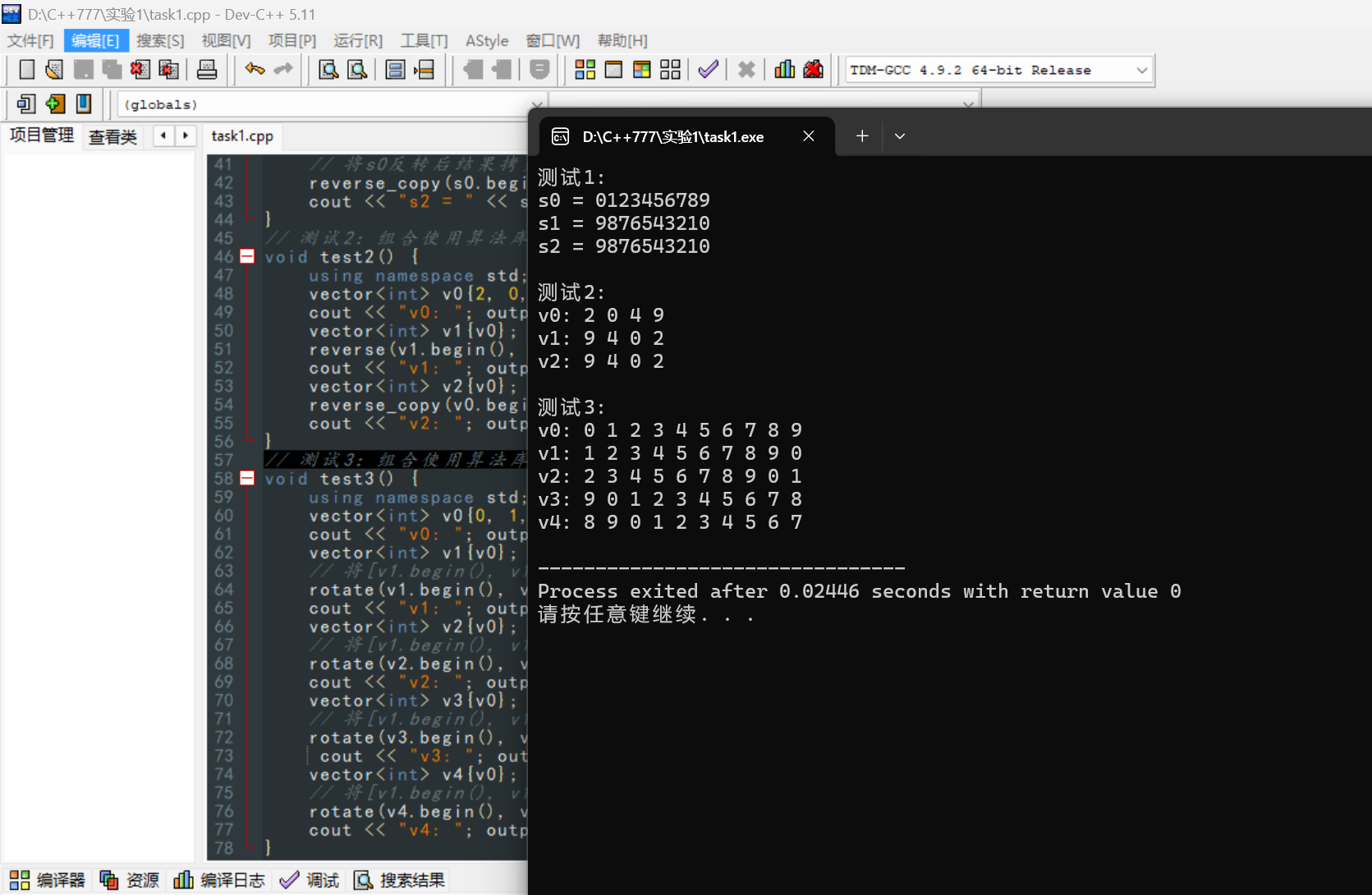
问题回答1-1

reverse 直接修改原容器，而 reverse_copy 生成反转后的副本，原容器不变，需要额外的输出迭代器。

问题回答1-2

rotate根据middle指针把区间[first,last)拆成两段[first,middle)和[middle,last)，然后把后段移到前段前面，前段移动到后段后面，得到新的字符串。

first：待操作区间的起始迭代器，middle：新的起始点，last：代操作区间的结束位置+1。

 实验任务2

代码2

#include <iostream>
#include <vector>
#include <algorithm>
#include <numeric>
#include <iomanip>
#include <cstdlib>
#include <ctime>
// 模板函数声明
template<typename T>
void output(const T &c);
int generate_random_number();
void test1();
void test2();
int main() {
    std::srand(std::time(0));    // 添加随机种子
    std::cout << "测试1: \n";
    test1();
    std::cout << "\n测试2: \n";
    test2();
}
// 输出容器对象c中的元素
template <typename T>
void output(const T &c) {
    for(auto &i: c)
        std::cout << i << ' ';
    std::cout << '\n';
}
// 返回[0, 100]区间内的一个随机整数
int generate_random_number() {
    return std::rand() % 101;
}
// 测试1：对容器类对象指定迭代器区间赋值、排序
void test1() {
    using namespace std;
    vector<int> v0(10);// 创建一个动态数组对象v0, 对象大小为10
    generate(v0.begin(), v0.end(), generate_random_number); // 生成随机数填充v0
    cout << "v0: "; output(v0);
    vector<int> v1{v0};
    sort(v1.begin(), v1.end()); // 对整个vector排序
    cout << "v1: "; output(v1);
    vector<int> v2{v0};
    sort(v2.begin()+1, v2.end()-1); // 只对中间部分排序，不包含首尾元素
    cout << "v2: "; output(v2);
}
// 测试2：对容器类对象指定迭代器区间赋值、计算最大值/最小值/均值
void test2() {
    using namespace std;
    vector<int> v0(10);
    generate(v0.begin(), v0.end(), generate_random_number); 
    cout << "v0: "; output(v0);
    // 求最大值和最小值
    auto min_iter = min_element(v0.begin(), v0.end());
    auto max_iter = max_element(v0.begin(), v0.end());
    cout << "最小值: " << *min_iter << endl;
    cout << "最大值: " << *max_iter << endl;
    // 同时求最大值和最小值
    auto ans = minmax_element(v0.begin(), v0.end());
    cout << "最小值: " << *(ans.first) << endl;
    cout << "最大值: " << *(ans.second) << endl;
    // 求平均值
    double avg1 = accumulate(v0.begin(), v0.end(), 0.0) / v0.size();
    cout << "均值: " << fixed << setprecision(2) << avg1 << endl;
    sort(v0.begin(), v0.end());
    double avg2 = accumulate(v0.begin()+1, v0.end()-1, 0.0) / (v0.size()-2);
    cout << "去掉最大值、最小值之后，均值: " << avg2 << endl;
}

运行截图2

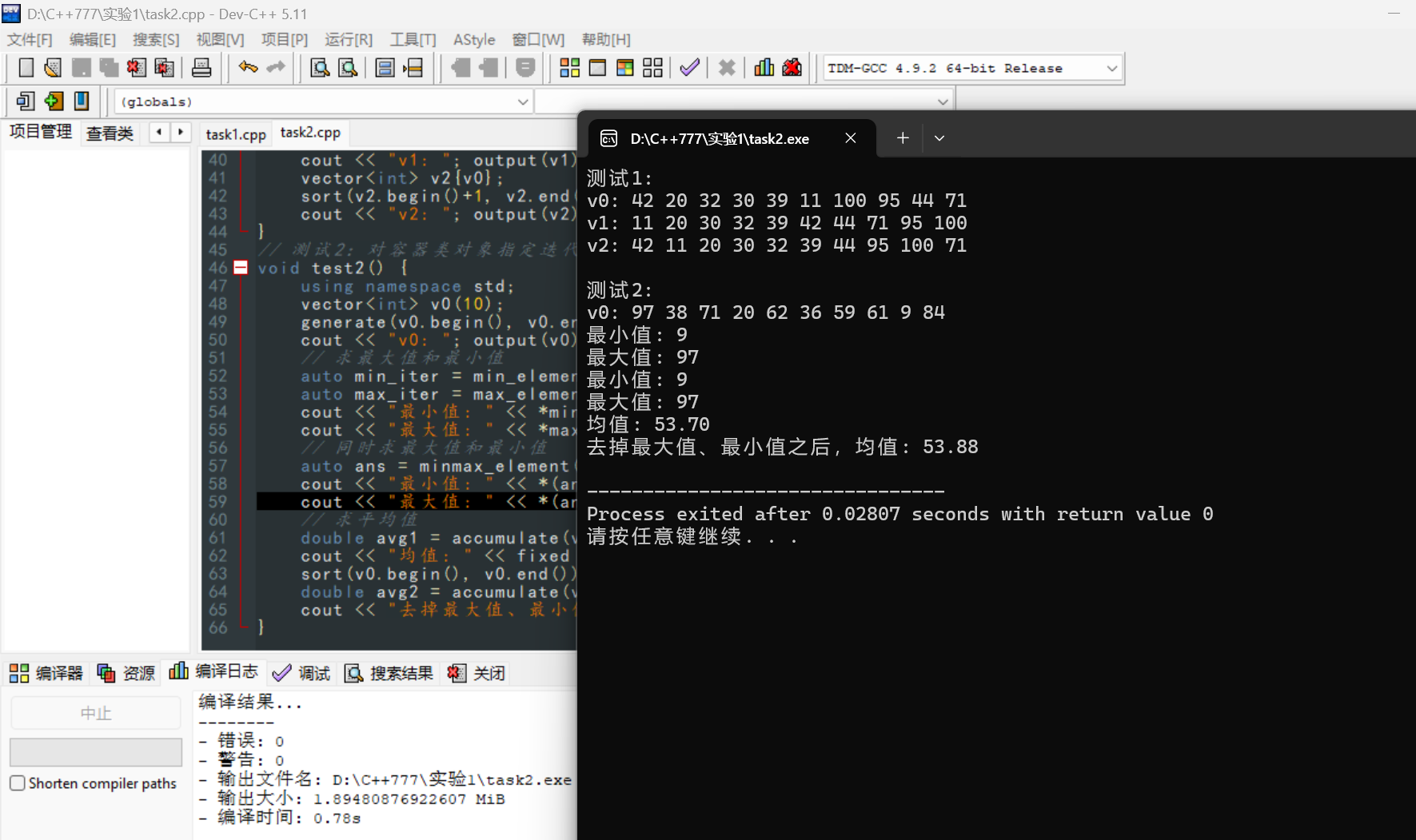
问题回答2-1

generate用于将区间[first,last)的元素，通过指定的函数生成的新值顺序赋值。

问题回答2-2

minmax_element只需要遍历一次区间，就可以同时找到最小值和最大值，而分别调用min_element和max_element需要对区间进行两次遍历；

使用前者只要写一遍逻辑，而使用后者需要写两次逻辑，所以前者也能使代码更简洁、清晰，而后者略显冗余。

问题回答2-3

相比于自定义函数，lambda的特点如下——无需单独定义一个函数，直接在调用处内嵌生成逻辑，所以更简洁；lambda表达式的作用范围只在调用的上下文中，不会有全局命名污染的问题。但也有些缺点，自定义函数有更好的代码复用性，而且当逻辑复杂时，自定义函数的可读性更高。所以lambda适用于生成器函数的逻辑较为简单且只在当前上下文使用，无需重复条用的情况，而自定义函数适用于生成器函数逻辑复杂，放在lambda表达式中会影响代码可读性的情况，以及该逻辑需要在多个地方使用时。其实有的时候为了方便单独测试也会把一个lambda表达式单独拎出来变成一个普通的函数。

实验任务3

代码3

#include <iostream>
#include <string>
#include <algorithm>
#include <cctype>
unsigned char func(unsigned char c);
void test1();
void test2();
int main() {
    std::cout << "测试1: 字符串大小写转换\n";
    test1();
    std::cout << "\n测试2: 字符变换\n";
    test2();
}
unsigned char func(unsigned char c) {
    if(c == 'z')
        return 'a';
    
    if(c == 'Z')
        return 'A';
    
    if(std::isalpha(c))
        return static_cast<unsigned char>(c+1);
    
    return c;
}
void test1() {
    std::string s1{"Hello World 2049!"};
    std::cout << "s1 = " << s1 << '\n';
    std::string s2;
    for(auto c: s1)
        s2 += std::tolower(c);
    std::cout << "s2 = " << s2 << '\n'; 
    std::string s3;
    for(auto c: s1)
        s3 += std::toupper(c);
    std::cout << "s3 = " << s3 << '\n'; 
}
void test2() {
    std::string s1{"I love cosmos!"};
    std::cout << "s1 = " << s1 << '\n';
    std::string s2(s1.size(), ' ');
    std::transform(s1.begin(), s1.end(), s2.begin(), func);
    std::cout << "s2 = " << s2 << '\n';
}

运行截图3

问题回答3-1

func的功能是传来的字母按照字母表顺序“循环递增”，但不改变大小写，且非字母保持不变。

问题回答3-2

tolower将字符转为小写字母，但非字母保持不变；toupper将字符转化为大写字母，但非字母保持不变。

问题回答3-3-1

第一个参数代表输入区间的起始迭代器；第二个参数代表输入区间的结束迭代器，且不包含该位置，第三个参数代表输出区间的起始迭代器，存储变换后的结果的起始位置；第四个参数即对每个输入元素执行的变换函数。

问题回答3-3-2

如果将s2.begin()改为s1.begin()，则输出结果会直接覆盖s1的内容，则s2中的内容不变，而s1中的内容被覆盖为转化后的情况。

实验任务4

代码4

#include <iostream>
#include <string>
#include <algorithm>
bool is_palindrome(const std::string &s);
bool is_palindrome_ignore_case(const std::string &s);
int main() {
    using namespace std;
    string s;
    // 多组输入，直到按下Ctrl+Z结束测试
    while(cin >> s) {
        cout << boolalpha 
            << "区分大小写: " << is_palindrome(s) << "\n"
            << "不区分大小写: " << is_palindrome_ignore_case(s) << "\n\n";
    }         
}
// 函数is_palindrome定义
// 待补足
// ×××
bool is_palindrome(const std::string &s) {
    auto left = s.begin(), right = s.end() - 1;
    while (left < right) {
        if (*left != *right) {
            return false;
        }
        ++left;
        --right;
    }
    return true; 
}
// 函数is_palindrome_ignore_case定义
// 待补足
// ×××
bool is_palindrome_ignore_case(const std::string &s) {
    auto left = s.begin(), right = s.end() - 1;
    while (left < right) {
        if (std::tolower(*left) != std::tolower(*right)) {
            return false;
        }
        ++left;
        --right;
    }
    return true; 
}

运行截图4

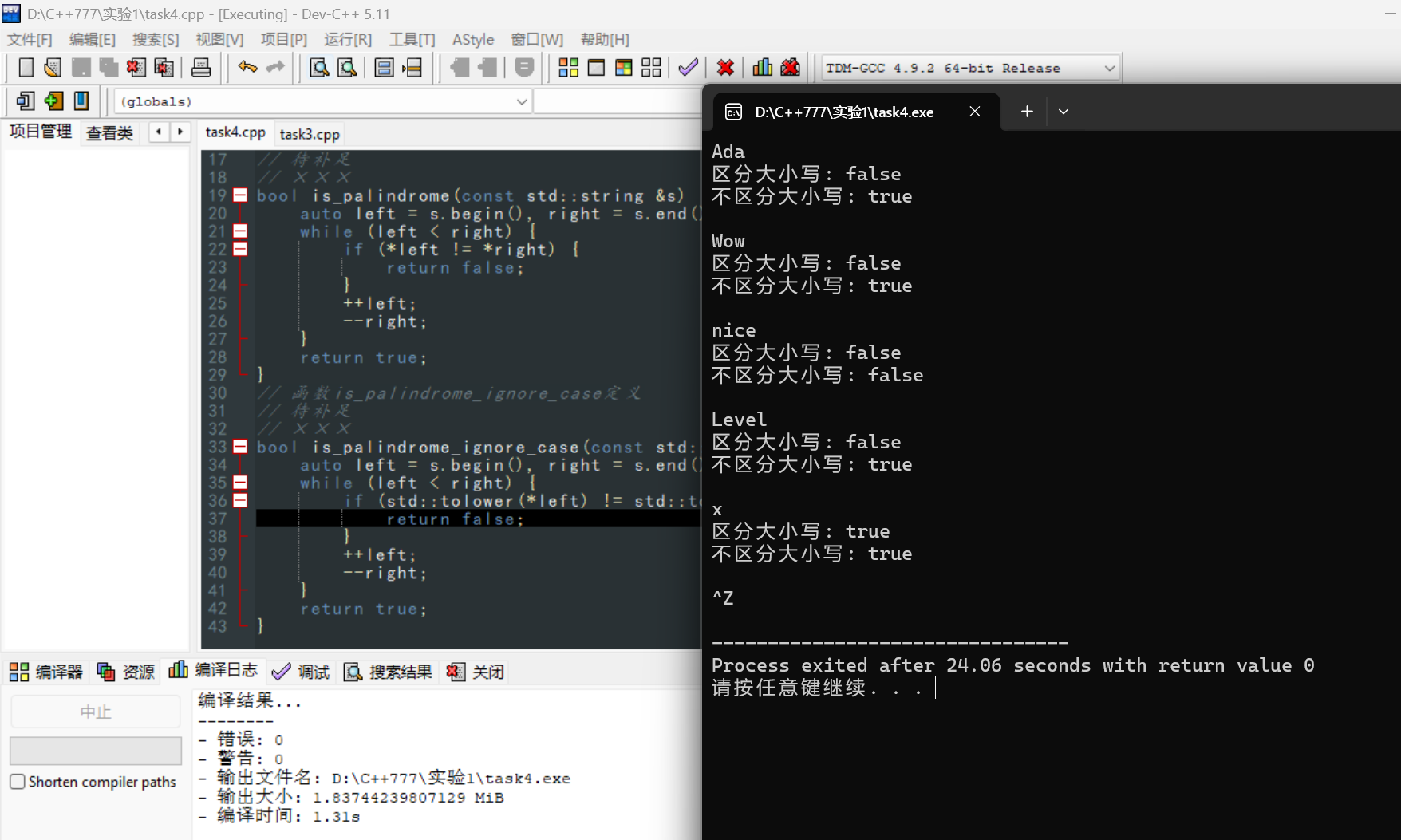
问题回答4

可以改用std::getline(cin, s)，会读取整行的输入，包括空格，直到遇到换行符为止。

 

实验任务5

代码5

#include <iostream>
#include <string>
#include <algorithm>
std::string dec2n(int x, int n = 2);
int main() {
    int x;
    while(std::cin >> x) {
    std::cout    << "十进制: " << x << '\n'
                << "二进制: " << dec2n(x) << '\n'
                << "八进制: " << dec2n(x, 8) << '\n'
                << "十二进制: " << dec2n(x, 12) << '\n'
                << "十六进制: " << dec2n(x, 16) << '\n'
                << "三十二进制: " << dec2n(x, 32) << "\n\n"; 
    }
}
// 函数dec2n定义
// 待补足
// ×××
inline char digit(int num)
{
    return (num < 10)?(num + '0'):(num - 10 + 'A');
}
std::string dec2n(int x, int n) {
    std::string answer;
    do {
        answer.push_back(digit(x % n));
        x /= n;
    }
    while(x != 0);
    reverse(answer.begin(), answer.end());
    return answer;
}

运行截图5

实验任务6

代码6

#include<iostream>
#include <iomanip>
int main()
{
    using std::cout;
    using std::endl;
    using std::setw;
    using std::setfill;
    cout << "  ";
    for (char i = 'a'; i <= 'z'; i++) {
        cout << " " << i;
    }
    char c = 'A';
    for (int i = 1; i <= 26; i++) {
        cout << endl << setw(2) << setfill(' ') << i;
        c++;
        if (c > 'Z') c = 'A';
        for (int j = 1; j <= 26; j++) {
            cout << " " << c++;
            if (c > 'Z') c = 'A';
        }
    }
}

运行截图6

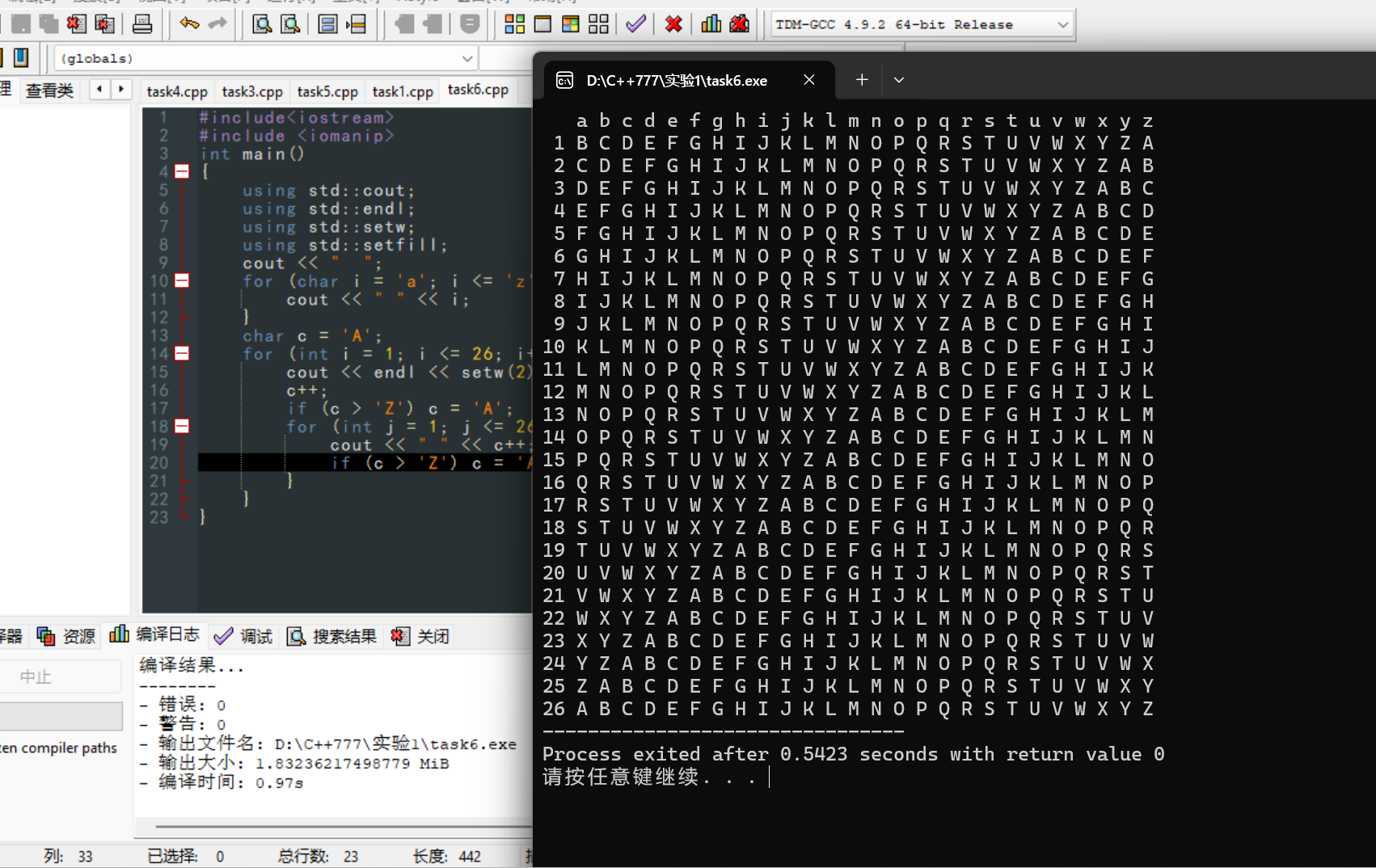
实验任务7

代码7

//尽量保证每种算术都有，且除法的生成效果更好
#include<iostream>
#include <cstdlib>
#include <ctime>
inline char Symbol(int x)
{
    switch(x) {
        case 0: return '+';
        case 1: return '-';
        case 2: return '*';
        case 3: return '/';
    }
}
inline int Rand10()
{
    return rand() % 10 + 1;
}
int getSymbol() // 确保每种符号都训练到，且每种符号算式保底数量为2 
{
    static int a[10] = {0, 0, 1, 1, 2, 2, 3, 3};
    static bool is_generated = false;
    static int which_symbol = 0;
    if (!is_generated) {//和扫雷高效生成雷区的思路差不多 
        for (int i = 0; i < 10; i++) {
            if (i > 7) {
                a[i] = rand() % 4;
            }
            int brief = a[i], choice = rand() % 10;
            a[i] = a[choice];
            a[choice] = brief;
        }
        is_generated = true;
    }
    return a[which_symbol++];
}
int main()
{
    using std::cout;
    using std::cin;
    using std::endl;
    srand(time(0));
    int right = 0;
    for (int i = 1; i <= 10; i++)
    {
        int digit, a, b, ans, myAns;
        switch (digit = getSymbol())
        {
            case 0: //加法 
                a = Rand10();
                b = Rand10();
                ans = a + b;
                break;
            case 1: //减法 
                a = Rand10();
                b = rand() % a + 1; //减数小于等于被减数 
                ans = a - b;
                break;
            case 2: //乘法 
                a = Rand10();
                b = Rand10();
                ans = a * b;
                break;
            case 3: //除法
                /*
                我之前写过一个版本，它只能满足题意，但生成效果并不理想，有没有一种更好的生成方式呢？ 
                除法分为两类，第一类为形式 n / 1 = n 或者形式 n / n = 1
                如果随机抽取，则抽取到这种的可能性较大，但它的训练意义很鸡肋
                第二类在被除数10以内的限制下只有8种，打表都可以
                4 / 2 = 2 ；6 / 2 = 3 ；6 / 3 = 2 ；8 / 2 = 4 ；8 / 4 = 2 ；9 / 3 = 3 ；10 / 2 = 5 ；10 / 5 = 2；
                这一类更具有训练意义
                我们知道生成的除法的数量是2~4 ，因为我们生成时保证了每种运算的训练都至少2个 
                所以我们希望第一类和第二类至少都要有，但第一类不超过2个，且为2时包含其两种形式 
                思路就是记忆第一类生成的个数和第其一次生成时采用的形式，以及第一次生成的是谁
                1.第一次生成完全随机，
                2.如果是第二次生成，则先和第一次生成的结果不在同一类
                3.如果第一类且其个数已经为2，则改为生成第二类 
                4.如果是第二次生成第一类，则必然与其第一次的形式不同 
                */ 
                static int generate_times = 0, type0times = 0, type1times = 0, first_type, type, first_type0_mode = -1;
                if (!generate_times) {
                    type = first_type = rand() % 2;
                }
                else {
                    if (generate_times == 1) {
                        type = (1 + first_type) % 2;
                    }
                    else if (type0times > 1) {
                        type = 1;
                    }
                    else {
                        type = rand() % 2;
                    }
                }
                int type0_mode;
                if (type == 0) {
                    if (first_type0_mode == -1) {
                        first_type0_mode = rand() % 2;
                        type0_mode = first_type0_mode;    
                    }
                    else {
                        type0_mode = (1 + first_type0_mode) % 2;
                    }
                    if (type0_mode == 0) {
                        a = Rand10(), b = 1, ans = a;
                    }
                    else {
                        a = Rand10(), b = a, ans = 1;
                    }
                }
                else {
                    static int type1_mode_available[8] = {1, 2, 3, 0, 0, 0, 0, 0}; //初始化就考虑周全，避免重复 
                    static int type1_mode[3];
                    if (!type1times) {
                        for (int j = 0; j < 3; j++) {
                        int brief = type1_mode_available[j], choice = rand() % 8;
                        type1_mode_available[j] = type1_mode_available[choice];
                        type1_mode_available[choice] = brief;
                        }
                        for (int j = 0; j < 8; j++) {
                            if (type1_mode_available[j]) {
                                type1_mode[type1_mode_available[j] - 1] = j;
                            }
                        }
                    }
                    switch(type1_mode[type1times++])
                    {
                        case 0:
                            a = 4, b = 2;
                            break;
                        case 1:
                            a = 6, b = 2;
                            break;
                        case 2:
                            a = 6, b = 3;
                            break;
                        case 3:
                            a = 8, b = 2;
                            break;
                        case 4:
                            a = 8, b = 4;
                            break;
                        case 5:
                            a = 9, b = 3;
                            break;
                        case 6:
                            a = 10, b = 2;
                            break;
                        case 7:
                            a = 10, b = 5;
                    }
                    ans = a / b;
                }
                generate_times++;
        }
        cout << a << " " << Symbol(digit) << " " << b << " = ";
        cin >> myAns;
        if (myAns == ans) {
            right++;
        }
    }
    cout << "正确率：" << right * 10 << ".00%"; //小心！正确率为0时不能输出成00.00% 
}

运行截图7-1

运行截图7-2

运行截图7-3

五、实验总结

这次实验最令我思考的是实验7，因为这个任务相对开放，一开始我使用了一种很简便的方式就实现了实验的要求，但是我注意到有一定概率10道题里有概率会有一种运算较少甚至没有，所以在符号生成部分我设计了一个优化的实现，保证10道题里每种运算至少有2道；其次我注意到除法的生成常规的实现方式效果不理想，总是出现n/1=n或n/n=1的形式，而三个数里不含1的形式较少，我就详细分析了其成因，发现是因为被除数的范围实在太小，于是我设计了一个有保底的随机生成策略，使得每次10道题里这几种除法算式能均衡地生成。

前面的实验让我比较有收获的是发现有很多方法可以拿来直接用，不需要自己动手写。

比较遗憾的是由于时间问题，实验7没有写成面向对象的程序设计形式，所以其可移植性不高，所以我让AI帮我改了一下实现方式，但不改变逻辑，经过我的学习和调试，发现这个代码能跑，且我觉得它挺棒的，所以我想把它分享在最后。

#include <iostream>
#include <array>
#include <vector>
#include <random>
#include <algorithm>

class SymbolSequence {
public:
    SymbolSequence(std::mt19937 &rng) : rng_(rng) { init(); }

    int next() {
        if (index_ < seq_.size()) return seq_[index_++];
        // 防御：如果意外请求超过10个，循环返回最后一个
        return seq_.back();
    }

    static char toChar(int symbol) {
        switch (symbol) {
            case 0: return '+';
            case 1: return '-';
            case 2: return '*';
            case 3: return '/';
            default: return '?';
        }
    }

private:
    void init() {
        // 与原逻辑一致：先设定前8个保证每种运算至少2次，后两个随机，
        // 然后按原算法逐步随机交换，得到长度为10的排列/组合
        seq_ = {0, 0, 1, 1, 2, 2, 3, 3, 0, 0};
        std::uniform_int_distribution<int> pick10(0, 9);
        for (size_t i = 0; i < seq_.size(); ++i) {
            if (i > 7) seq_[i] = pick4();
            int choice = pick10(rng_);
            std::swap(seq_[i], seq_[choice]);
        }
    }

    int pick4() { return std::uniform_int_distribution<int>(0, 3)(rng_); }

    std::array<int, 10> seq_;
    std::size_t index_ = 0;
    std::mt19937 &rng_;
};

class DivisionGenerator {
public:
    DivisionGenerator(std::mt19937 &rng) : rng_(rng) {}

    // 生成除法题（按原逻辑保证第一类/第二类分布与顺序）
    void generate(int &a, int &b, int &ans) {
        int type; // 0 = 第一类 (n/1 或 n/n)，1 = 第二类（打表的8种）
        if (generate_times_ == 0) {
            type = first_type_ = uniform2();
        } else if (generate_times_ == 1) {
            type = (1 + first_type_) % 2;
        } else if (type0times_ > 1) {
            type = 1;
        } else {
            type = uniform2();
        }

        if (type == 0) {
            int type0_mode;
            if (first_type0_mode_ == -1) {
                first_type0_mode_ = uniform2();
                type0_mode = first_type0_mode_;
            } else {
                type0_mode = (1 + first_type0_mode_) % 2;
            }
            if (type0_mode == 0) {
                a = rand10(); b = 1; ans = a;
            } else {
                a = rand10(); b = a; ans = 1;
            }
            ++type0times_;
        } else {
            if (type1times_ == 0) {
                prepare_type1_modes();
            }
            int mode = type1_modes_[type1times_++];
            switch (mode) {
                case 0: a = 4;  b = 2; break;
                case 1: a = 6;  b = 2; break;
                case 2: a = 6;  b = 3; break;
                case 3: a = 8;  b = 2; break;
                case 4: a = 8;  b = 4; break;
                case 5: a = 9;  b = 3; break;
                case 6: a = 10; b = 2; break;
                case 7: a = 10; b = 5; break;
                default: a = 10; b = 2; break;
            }
            ans = a / b;
        }
        ++generate_times_;
    }

private:
    int uniform2() { return std::uniform_int_distribution<int>(0, 1)(rng_); }
    int rand10() { return std::uniform_int_distribution<int>(1, 10)(rng_); }

    void prepare_type1_modes() {
        // 从0..7中随机选择3个不同的序号（与原实现等价）
        std::vector<int> pool(8);
        for (int i = 0; i < 8; ++i) pool[i] = i;
        std::shuffle(pool.begin(), pool.end(), rng_);
        type1_modes_.assign(pool.begin(), pool.begin() + 3);
    }

    std::mt19937 &rng_;
    int generate_times_ = 0;
    int type0times_ = 0;
    int type1times_ = 0;
    int first_type_ = 0;
    int first_type0_mode_ = -1;
    std::vector<int> type1_modes_;
};

class ProblemGenerator {
public:
    ProblemGenerator(std::mt19937 &rng) : rng_(rng), seq_(rng), divgen_(rng) {}

    // 生成一题（返回运算类型、操作数与答案）
    void next(int &symbol, int &a, int &b, int &ans) {
        symbol = seq_.next();
        if (symbol == 0) { // 加
            a = rand10(); b = rand10(); ans = a + b;
        } else if (symbol == 1) { // 减，保证被减数 >= 减数
            a = rand10();
            b = std::uniform_int_distribution<int>(1, a)(rng_);
            ans = a - b;
        } else if (symbol == 2) { // 乘
            a = rand10(); b = rand10(); ans = a * b;
        } else { // 除 （调用复杂逻辑）
            divgen_.generate(a, b, ans);
        }
    }

    static char symbolChar(int s) { return SymbolSequence::toChar(s); }

private:
    int rand10() { return std::uniform_int_distribution<int>(1, 10)(rng_); }

    std::mt19937 &rng_;
    SymbolSequence seq_;
    DivisionGenerator divgen_;
};

int main() {
    std::mt19937 rng((std::random_device())());
    ProblemGenerator gen(rng);

    int right = 0;
    for (int i = 0; i < 10; ++i) {
        int symbol, a, b, ans;
        gen.next(symbol, a, b, ans);

        std::cout << a << " " << ProblemGenerator::symbolChar(symbol) << " " << b << " = ";
        int myAns;
        if (!(std::cin >> myAns)) {
            // 非法输入或 EOF 时安全退出
            std::cerr << "\n输入错误，程序退出。\n";
            return 1;
        }
        if (myAns == ans) ++right;
    }

    // 与原输出保持一致（每题占10%，保留 .00）
    std::cout << "正确率：" << (right * 10) << ".00%";
    return 0;
}