关于图的一点东西

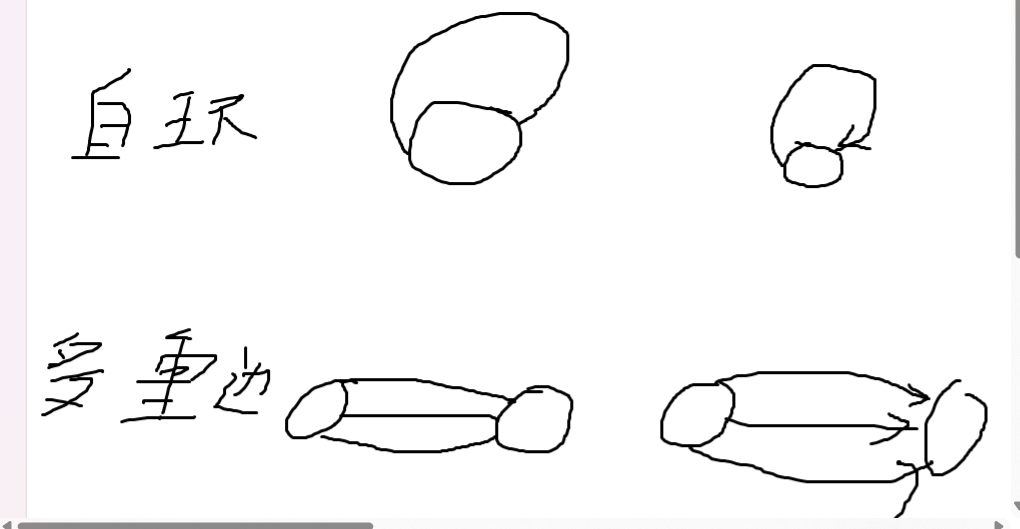
 自环的应用比如说在一个网页界面，我可以点击一个跳转到当前业面的链接，形成自环。

多重边的应用比如飞机航班，一个地方到另一个地方可以有多条航线，这些航线的属性比如价格，时间等会有不同。

图可以表示为G=(V,E)，V表示顶点集，E表示边集，|V|表示顶点的数量，|E|表示边的数量。G就是有序对。
无权图就是权重为1的有权图
城际交通路可以看作加权无向图，社交网络可以看作非加权无向图，万维网为非加权有向图。一个无向图可以化为有向图，反之不行。。

不含有自环或者多重环的图是简单图。
对于有向的简单图而言，当|V|=n时,0<=|E|<=n*(n-1).
无向的简单图而言，当|V|=n,0<=|E|<=(n*(n-1))/2
如果一个图的边数越接近顶点数的平方，就说明这个图越密集，反之越稀疏。对于越密集和稀疏的图，使用不同的数据结构存储，前者多用邻接矩阵，后者多用邻接表。

一个path指没有顶点或者边重复的途径。
一个walk指允许重复的途径。
一个trail就是说顶点可以重复，但是边不允许重复。通常说路径指的就是简单路径
就是path。

如果任何一个顶点都可以到达任意一个顶点，对于满足这个要求的无向图说connected，
对于满足这个要求的有向图说strongly connected强连接。

对于closed walk，就是说开始和结束都在一个相同的节点上，并且经过的边数大于0。
一个二叉树就是一个无向无环图，而把有向无环图称为DAG(Directed acyclic Graphs)
acyclic就是没有环路的意思。

数据结构的宗旨就是，对于最频繁的操作，一定要让它的耗费时间最低。另外空间尽量小

对于图的表示法，边列表表示法，开辟2个数组，1个存储顶点的名称比如A,B啥的，1个存储边的信息(即当前边，与其连接的1个边，这条边的权重)，Edge的话用结构体或类表示，三个元素，可以直接用char*去指向名称字符串的地址，也可string，不过char*比string好点，string要拷贝，，当然更好一点的话，类里用int表示起始点和终点，然后用第一个数组的下标替代名称字符串。这样空间是O(|V|+|E|),如果要查一个节点的邻接节点，就得遍历第二个数组，时间O（|E|）对于简单图来说就O(n^2)，很慢。如果是O（|V|）就好了。

ok，第二种邻接矩阵表示法。（示例为无向无权）存储顶点的名称的数组不变，然后用一个二维数组(大小为|V|*|V|)，K(ij)=1表示第一个数组里下标为i的节点与下标为j的节点相连，如果不相连置0即可，按这样的话那么对于无向图来说这个矩阵就是对称的因为有kij就有kji，那么这时候如果我们想知道一个节点的邻接节点的话，只需要从第一个数组里得到那个节点的下标，然后遍历邻接矩阵的某一行即可时间就是O(V),当然为了不每次遍历第一个数组，可以用unordered_map，key是节点名称，value是节点下标，那么每次查询下标就是O(1)。 如果想知道两个节点是否相连O(1)+O(1),非常快。 对于无向带权图，只需要在邻接矩阵里对应位置写权，其他位置弄一个不可能的数就行。 但是邻接矩阵的缺点就是如果V很大，并且E很小，也就是稀疏图而言，矩阵的空间被大量浪费，如果是密集图还好可以充分利用，但是现实里基本都是稀疏图，比如QQ啥的社交网络，那么多用户，你不可能和每个人都有联系，所以基本都是稀疏图。

如果V足够大，那么现实里|E|<<|v|.

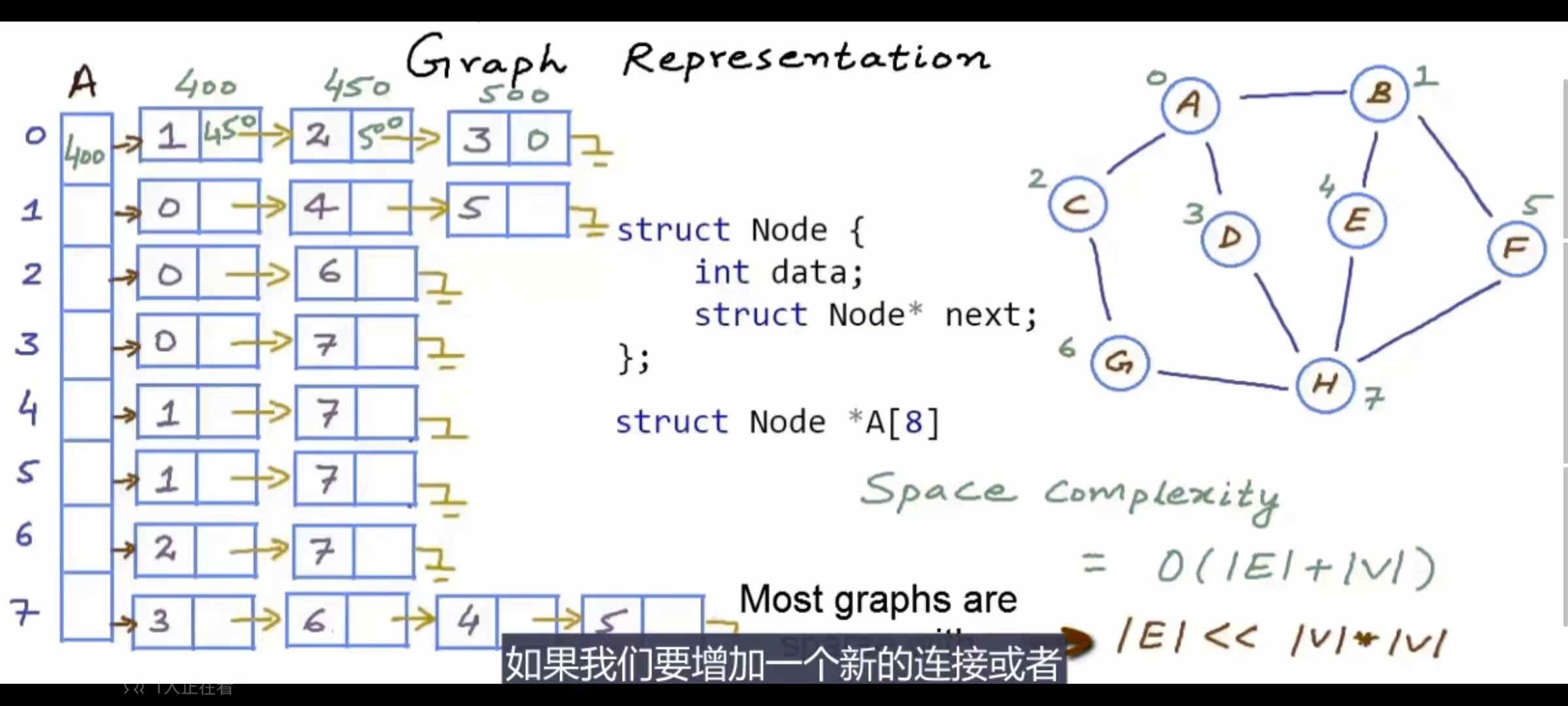
ok，第三种邻接表 表示法。(示例为无向无权图)存储顶点的名称的数组不变，然后搞一个指针数组int*[]A，然后每个指针指向不同的一维数组，那么A[0][k],就表示第一个数组里下标为0的那个名称的节点与下标A[0][K]的节点相连，此时A[0]的那个一维数组的下标没有用，它的内容有用。这样的话如果想要知道两个节点是否相连，那么仍然unordered_map确保找到那个节点下标为O(1)，但是还是得遍历A[下标]的数组，而且你不能保证我的这个数组就是有序的，（如果有序可以二分O(log2(n))但是每次要排序很麻烦)，所以时间复杂度为O(V)（讨论最坏情况下）。 如果想知道一个节点的所以邻接节点，那么一样还得去遍历那个A[下标]的数组，时间为O(v),但是其实实际来看由于大多是稀疏图，所以遍历的效率仍然远远高于邻接矩阵的按行遍历。

但是上面的一维数组表示的flexibility<<链表表示的flexibility<<二叉搜索树表示的flexibility

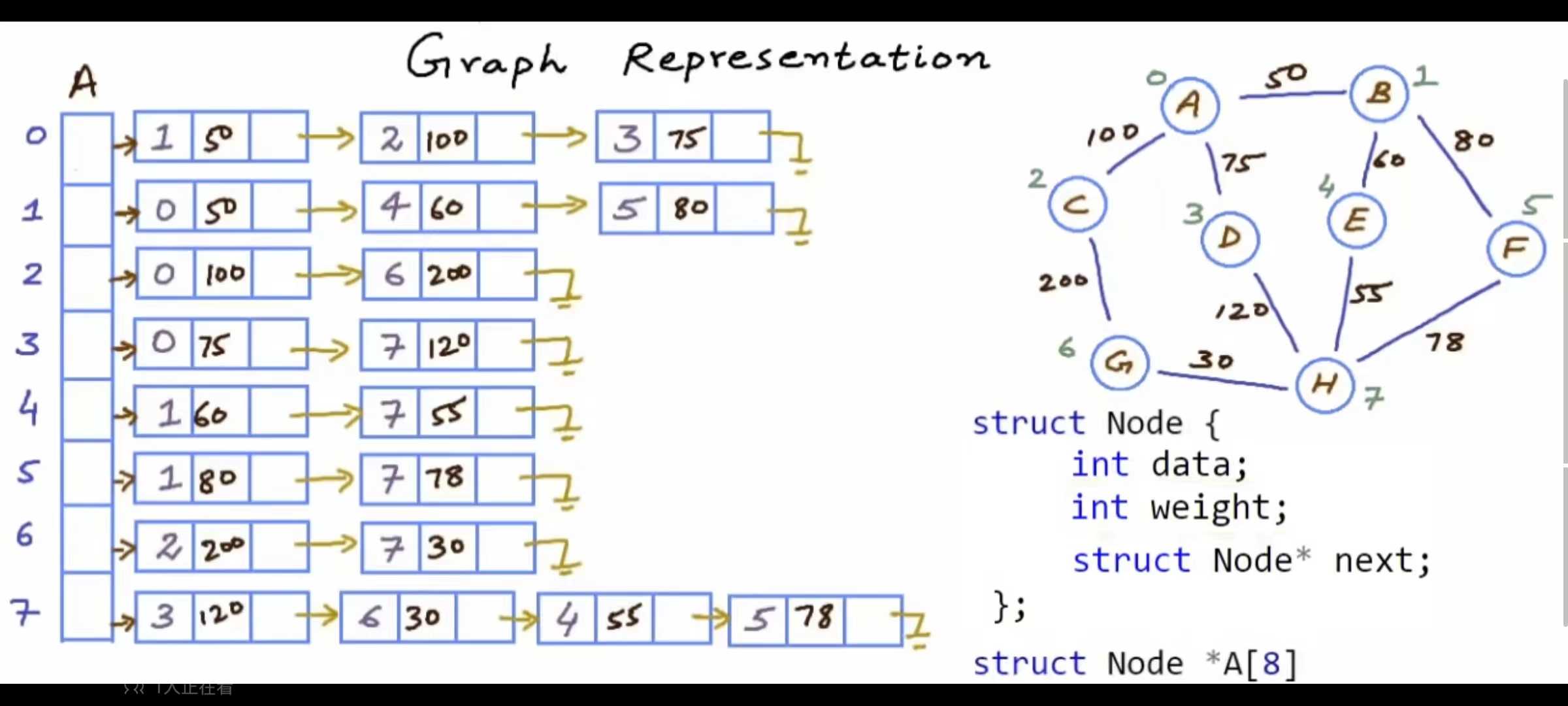
因为如果要求增删的话，邻接矩阵就是定位好后 0->1 1->0即可,就是O(1),单数如果一维数组的话就得扩增数组大小不好，所以换为链表，免除了扩展数组的烦恼并且尾插时间是O(当前这个链表里的个数),删除的话先定位其实时间也一样，效率没变，但是可以给struct加权了(无向有权也ok)，那么还能不能再次改善呢？没错构建二叉搜索树，BstNode*A[k],A[k]里就是指向root的头结点，那样的话如果有权我可以向struct里加属性，而且一个平衡的二叉搜索树搜索节点的效率是O(log2(n))，遍历的话就是O(|E|)，插入是O(log2(n)),就是说树的相关操作其实和其高度是密不可分的，一个平衡的二叉搜索树的高度差不多就是log2(n)，所以删除的时间和空间也是O(log2(n))。

只有平衡的二叉搜索树的高度才是log2(n),AVI树和红黑树就是这种情况。

 

 

邻接矩阵 邻接表 邻接矩阵 邻接表(数组)
时间复杂度 时间复杂度 空间复杂度 空间复杂度

判断2个节点是否相连 1 |E(该节点的)| |V|+|V*V| |V|+|E|
遍历一个节点邻接节点 |V| |E(该节点的)|
增 1 |E(该节点的)|
删 1 |E(该节点的)|