2019年广东外语外贸大学程序设计竞赛（新手赛）-F题（好快的刀）题解

题面：

 

 

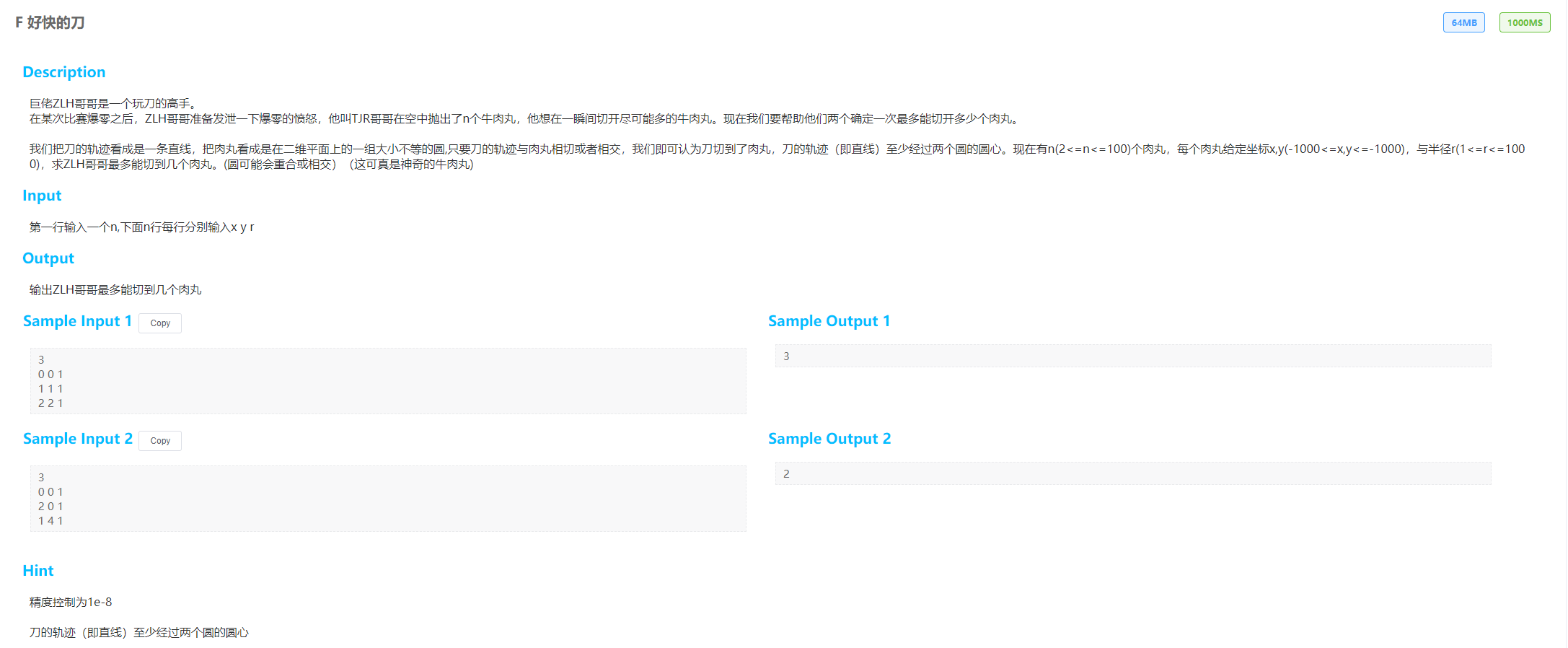
题目意为，任意连接两个圆的圆心形成一条直线，计算与该直线相交或相切的圆的数量，求这些直线最多能相交或相切多少个圆

解题思路：

遍历所有的圆，计算出两圆圆心生成的直线，再遍历其他的圆，检测这些圆的半径与圆心到直线的距离，即可确认直线与圆的关系。

坑点：

用函数思路解决时，需考虑斜率不存在问题（用向量解决即可规避该问题）

所有圆均为同心圆时，需特判（比赛测试数据并未考虑该特殊情况，赛后由广州大学的一位大佬发现，特此感谢）

标程：

出题时分别用函数的方法和向量的方法手搓了两份代码，最后用的标程是用kuangbin模板写的

向量的方法精度比函数的方法精度要高，但为降低难度还是放宽了精度的范围（大师兄说年轻人不能太毒瘤）

#include <iostream>
#include <cmath>
using namespace std;
const double eps=1e-8;
const double inf =1e20;
//const double pi=acos(-1.0);
int sgn(double x){
    if(fabs(x)<eps) return 0;
    if(x<0) return -1;
    else return 1;
}
struct Point{
    double x,y;
    Point(){}
    Point(double _x,double _y){
        x=_x;
        y=_y;
    }
    void input(){
        scanf("%lf%lf",&x,&y);
    }
    bool operator ==(Point b)const{
        return sgn(x-b.x)==0&&sgn(y-b.y)==0;
    }
    Point operator -(const Point &b)const{
        return Point(x-b.x,y-b.y);
    }
    double operator ^(const Point &b)const{
        return x*b.y-y*b.x;
    }
    double distance(Point p){
        return hypot(x-p.x,y-p.y);
    }
};
struct Line{
    Point s,e;
    void input(){
        s.input();
        e.input();
    }
    double length(){
        return s.distance(e);
    }
    double dispointtoline(Point p){
        return fabs((p-s)^(e-s))/length();
    }
};
struct circle{
    Point p;
    double r;
    void input(){
        p.input();
        scanf("%lf",&r);
    }
    bool operator ==(circle v){
        return (p==v.p);
    }
    int relationline(Line v){
        double dst=v.dispointtoline(p);
        if(sgn(dst-r)<0) return 2;
        else if(sgn(dst-r)==0) return 1;
        else return 0;
    }
    
};
int main(){
    int n,ans(2),cou,flag(0);
    circle cir[105];
    Line line1;
    cin>>n;
    for(int i=0;i<n;i++) cir[i].input();
    for(int i=0;i<n;i++){
        if(cir[i]==cir[0]&&i==n-1)flag=1;
    }
    if(flag){
        cout<<n<<'\n';
        return 0;
    }
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            cou=2;
            if(i==j) continue;
            line1.e=cir[i].p;
            line1.s=cir[j].p;
            for(int k=0;k<n;k++){
                if(k==i||k==j) continue;
                if(cir[k].relationline(line1)!=0) cou++;
            }
            ans=max(ans,cou);
        }
    }
    cout<<ans<<'\n';
    return 0;
}

最后非常抱歉出题时没有考虑到同心圆的特殊情况，导致测试数据不够完善，特此致歉。