【纪中受难记】C3D2：数学大赏

跟我搞数学？还是算了吧。因为我太菜。

 

 

Description

 

Input

从文件a.in中读入数据。
第丬行两个整数n, m，意义见问题描述。
接下来m行，第i行三个整数x, y, z，表示第i个坑的坐标(x, y, z)。

Output

输出到文件a.out中
一个整数，即答案。 
 

Sample Input

2 3
1 0 1
1 1 1
0 2 0

Sample Output

36
 

Data Constraint

 

一直揪着n^3算法是迟早会错的。

考虑m^2算法：

　　对每一个限制，可以证明:

　　

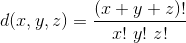
　　如果路上还有别的点，就是:

　　

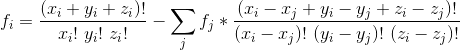
　　递推即可。

　　但T掉了。

　　先意思一下（60pts）：

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 int read(){
 4     int x=0,f=1;
 5     char c=getchar();
 6     while(!isdigit(c)){
 7         if(c=='-') f=-1;
 8         c=getchar();
 9     }
10     while(isdigit(c)){
11         x=(x<<1)+(x<<3)+(c^48);
12         c=getchar();
13     }
14     return x*f;
15 }
16 const int mod=1e9+7;
17 typedef long long ll;
18 const int M=5010;
19 ll mul[400010];
20 inline void init(){
21     mul[0]=mul[1]=1;
22     for(int i=2;i<=400000;i++){
23         mul[i]=(mul[i-1]*i)%mod;
24     }
25 }
26 inline ll qp(ll x,ll p){
27     ll res=x,ans=1;
28     while(p){
29         if(p&1) ans=(ans*res)%mod;
30         res=(res*res)%mod;
31         p>>=1;
32     }
33     return ans;
34 }
35 inline ll inv(ll x){
36     return qp(x,mod-2);
37 }
38 inline ll num(int x,int y,int z){
39     return (((((mul[x+y+z]*inv(mul[x]))%mod)*inv(mul[y]))%mod)*inv(mul[z]))%mod;
40 }
41 struct node{
42     int x,y,z;
43     bool operator < (const node &t)const{
44         if(x==t.x){
45             if(y==t.y){
46                 return z<t.z;
47             }
48             else return y<t.y;
49         }
50         else return x<t.x;
51     }
52 }a[M];
53 ll f[M];
54 ll sig[M];
55 int n,m;
56 int main(){
57     freopen("a.in","r",stdin);
58     freopen("a.out","w",stdout);
59     init();
60     n=read(),m=read();
61     for(int i=1;i<=m;i++){
62         a[i].x=read();
63         a[i].y=read();
64         a[i].z=read();
65     }
66     sort(a+1,a+m+1);
67     for(int i=1;i<=m;i++){
68         f[i]=num(a[i].x,a[i].y,a[i].z);
69     }
70     for(int i=1;i<=m;i++){
71         for(int j=1;j<i;j++){
72             if(a[j].y<=a[i].y&&a[j].z<=a[i].z){
73                 sig[i]=(sig[i]+(f[j]*num(a[i].x-a[j].x,a[i].y-a[j].y,a[i].z-a[j].z))%mod)%mod;
74             }
75         }
76         f[i]=(f[i]-sig[i]+mod)%mod;
77     }
78     for(int i=1;i<=m;i++){
79         if(a[i].x==n&&a[i].y==n&&a[i].z==n) continue;
80         sig[0]=(sig[0]+(f[i]*num(n-a[i].x,n-a[i].y,n-a[i].z)%mod))%mod;
81     }
82     printf("%lld",(long long)(num(n,n,n)-sig[0]+mod)%mod);
83     return 0;
84 }

 

Description


 

Input

从文件c.in中读入数据.
不行一个正整数n和一个自然数m.

Output

输出到文件c.out中.
上行, 一个数表示答案. 
 

Sample Input

2 1

Sample Output

21
 

Data Constraint

第一眼，戳中盲区，来补一下矩阵吧！

 

矩阵变换是线性代数中矩阵的一种运算形式。

 

在线性代数中，矩阵的初等变换是指以下三种变换类型 ：

 

(1) 交换矩阵的两行（对调i,j，两行记为ri，rj）；

 

(2) 以一个非零数k乘矩阵的某一行所有元素（第i行乘以k记为ri×k）；

 

(3) 把矩阵的某一行所有元素乘以一个数k后加到另一行对应的元素(第j行乘以k加到第i行记为ri+krj)。

 

类似地，把以上的“行”改为“列”便得到矩阵初等变换的定义，把对应的记号“r”换为“c”。

 

矩阵的初等行变换与初等列变换合称为矩阵的初等变换。
（来自百度。）

矩阵的逆就是对矩阵A做任意次矩阵变换得到单位矩阵I，即：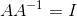

 

 

那么其中

 

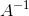
就是逆矩阵。

不过这道题和逆矩阵没有什么关系。

（只是可以这样写罢了，没什么分）

先给出结论：

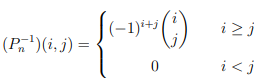
于是我们手推式子：

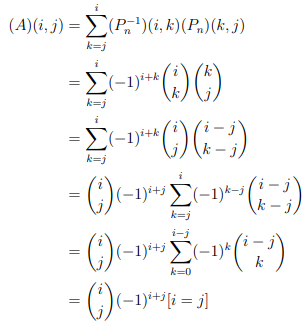
我觉得到这里还是能接受的。

所以对应将值算出来即可。

 

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 int read(){
 4     int x=0,f=1;
 5     char c=getchar();
 6     while(!isdigit(c)){
 7         if(c=='-') f=-1;
 8         c=getchar();
 9     }
10     while(isdigit(c)){
11         x=(x<<1)+(x<<3)+(c^48);
12         c=getchar();
13     }
14     return x*f;
15 }
16 typedef long long ll;
17 const int mod=1e9+7;
18 const int N=2e6+10; 
19 int n,m;
20 ll mul[N];
21 ll inv[N];
22 ll an;
23 ll qp(ll x,ll p){
24     ll res=x,ans=1;
25     while(p){
26         if(p&1) ans=(res*ans)%mod;
27         res=(res*res)%mod;
28         p>>=1;
29     }
30     return ans;
31 }
32 inline void init(){
33     inv[0]=inv[1]=1;
34     for(int i=2;i<=2000000;i++){
35         inv[i]=((mod-mod/i)*inv[mod%i])%mod;
36     }
37     mul[0]=mul[1]=1;
38     for(int i=2;i<=2000000;i++){
39         mul[i]=(mul[i-1]*inv[i])%mod;
40         inv[i]=(inv[i-1]*i)%mod;
41     }
42 }
43 ll c(int x,int y){
44     return (((inv[x]*mul[y])%mod)*mul[x-y])%mod;
45 }
46 int main(){
47     freopen("c.in","r",stdin);
48     freopen("c.out","w",stdout);
49     init();
50     n=read();m=read();
51     for(int i=1;i<=n;i++){
52         an=(an+(qp(i,2*m)*(c(2*i,i)-1))%mod)%mod;
53     }
54     printf("%lld",an);
55     return 0;
56 }

 

posted @ 2019-11-04 20:30  Nelson992770019  阅读(301)  评论(0)    收藏  举报