【Coursera Machine Learning】线性回归问题的梯度下降算法

引入

梯度下降算法可以用于在线性回归（及以外）问题中帮助我们求出最小的代价函数\(J\)。

基本步骤：先初始化\(\theta_0和\theta_1\)，一般选择同时初始化为0。然后持续改变\(\theta_0和\theta_1\)来减少代价函数\(J\)，直到最小值，或者是局部最小值。

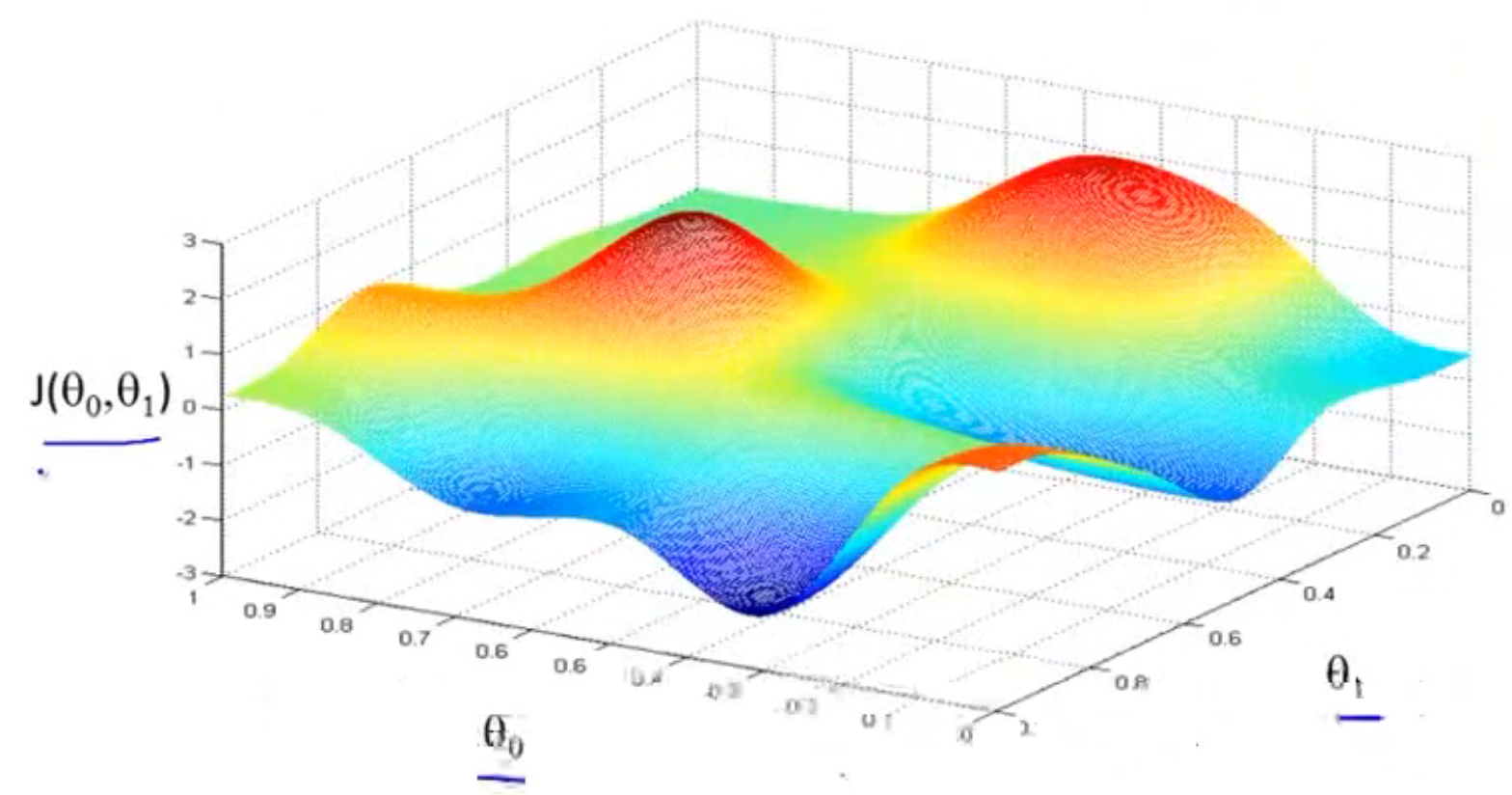
假设我们把下图现象成想象成一座山，想象你站在红色的山顶上，该用什么步伐和方向才能最快下山。如果你的起点偏移一点，你可能就会走截然不同的另外一条路，获得非常不同的局部最优解，这是梯度下降算法的特点之一。

定义

重复以下，直到收敛：

\[\theta_j:=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1)$$ for $$j=0$$ and $$j=1 \]

\[\partial$$：偏导数 $$:=$$：赋值 $$\alpha$$：一个数字，称为learning rate，用于控制在下山时的步伐长度 实线梯度下降算法时的微妙之处是你要在更新以上等式的同时更新$$\theta_0 和 \theta_1\]

赋值公式的解释

Learning Rate的含义

如果\(\alpha\)设置太小，向顶点靠拢的速度会很慢。

但反之如果\(\alpha\)太大，梯度下降法可能会掠过最低点，甚至最终无法收敛，甚至发散

偏导数项的含义

前面说过\(J\)关于单个变量，比如\(\theta_1\)的图像，是一条曲线，那么导数项的含义就是关于\(\theta_1\)为特定值时曲线的切线的斜率，将它带到公式里能让\(\theta_j\)的值向函数顶点（最低点），也就是我们要找的答案靠拢。

现在将代价函数公式代入梯度下降算法公式里，偏导数项就变成了以下形式：

\[\frac{\partial}{\partial\theta_j}\frac{1}{2m}\sum^m_1(h_\theta(x^{(i)})-y^{(i)})^2 \]

再将\(h_\theta\)带入，得：

\[\frac{\partial}{\partial\theta_j}\frac{1}{2m}\sum^m_1(\theta_0+\theta_1x^{(i)}-y^{(i)})^2 \]

如果θ一上来就在最低点会发生什么：如果上来就在最低点，那么导数项的斜率就是0，于是θ不会再有改变，维持在最低点。

于是可以分别求出\(\theta_0\)和\(\theta_1\)的偏导数项：

\(\theta_0\)：\(J=0\)

\[\frac{1}{m}\sum^m_1(h_\theta(x^{(i)})-y^{(i)}) \]

\(\theta_1\)：\(J=1\)

\[\frac{1}{m}\sum^m_1(h_\theta(x^{(i)})-y^{(i)})x^{(i)} \]

这两个微分项其实就是代价函数\(J\)的斜率，我们要在梯度下降算法中做的就是将上面两条式子反复重复直到收敛为止

使用梯度下降算法时，代价函数一定会是一个凸函数，所以最后结果一定能收敛到全局最优解。