图中欧拉回路数量

一本通上的问题。有一个这样的图：

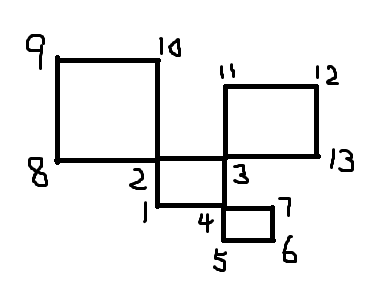求其中欧拉回路的数量，且重复的不算（以点来说，2-8-9-10和8-9-2-10是同一个）。

输入：

13 16  //13个点,16条边
9 10
9 8
8 2
10 2
2 3
2 1
1 4
3 4
11 3
11 12
12 13
13 3
4 7
4 5
5 6
6 7

输出：11

思路：以每个点为起点深搜，当再次遇到出发点时cnt++；

难点1：如何判断此条回路是否与某条重复？

解决方式：把曾经成功过的回路存在数组里，有新的成功回路时遍历一番。

难点2：邻接表+无向图，怎样存路径？

解决方式(重点)：边的结构体中带上其反向的那条边的序号；

难点3：怎样判断路径？

解决方式：1.如下文代码，把两点间两条边的序号都存下来，先排序，再比较——因为重复的话，与边的顺序无关；

　　　　　2.(重点)另一种思路，即把走过的边的bool标记存下来，不仅记录方便(memcpy即可，无需每一步记录)，比较时也方便。

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,m,x,y,xnt,la[105];
int str[105][205],sstr=1,snttr[105],snt,qq;//str是回路的记录,sstr是回路数量的记录,snttr是每个回路元素个数的记录 
struct Node{
	int lb,to,next;
}sid[105];
bool bd[205];
void ser(int a)
{
	if(a==qq&&snt)//qq是本次深搜的起点,a是当前点   snt是当前路线的元素个数, &&snt是考虑到未出发时a也是等于qq的 
	{
		bool flag=0;
		memcpy(str[sstr+1],str[sstr],sizeof str[sstr]);//排序前的存放在sstr+1里 
		sort(str[sstr]+1,str[sstr]+snt+1);
		for(int i=1;i<sstr;i++)//sstr是回路数量,现在遍历之前成功的回路 
			if(snttr[i]==snt)//当之前回路的元素个数与现在相等时进入(若不相等则不可能重复) 
			{
				bool fla=1;
				for(int j=1;j<=snt;j++)
					if(str[i][j]!=str[sstr][j])//有一个不相等,就fla=0 
					{
						fla=0;break;
					}
				if(fla)//fla==1说明这个和之前重复了 
				{
					flag=1;break;
				}
			}
		if(!flag)//flag==0说明这个没有和之前重复 
		{
			snttr[sstr]=snt;//存元素个数 
			sstr++;//刚才memcpy的sstr+1变成了sstr,即新的一条路的前面部分还是上一条路的
				   //就像从8字的交点出发,走完下面的圈后,继续向上走,这条继续的路的前面部分还是原来的那个下面的圈
				   //所以这条路成功了也不用return 
		}
		else
		{
			memcpy(str[sstr],str[sstr+1],sizeof str[sstr+1]);//把sstr变回排序前的样子(也许不需要?) 
			memset(str[sstr+1],0,sizeof str[sstr+1]);
		}
	}
	for(int i=la[a];i>0;i=sid[i].next)
		if(!bd[i]&&!bd[sid[i].lb])
		{
			bd[i]=1;
			bd[sid[i].lb]=1;//lb意义见输入过程注释 
			str[sstr][++snt]=i;
			str[sstr][++snt]=sid[i].lb;
			ser(sid[i].to);
			bd[i]=0;
			bd[sid[i].lb]=0;
			str[sstr][snt--]=0;
			str[sstr][snt--]=0;
		}
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++)
	{
		scanf("%d%d",&x,&y);
		xnt++;
		sid[xnt].lb=xnt+1;//用lb表示 9-10边 与 10-9边 这样的关系 
		sid[xnt].to=y;
		sid[xnt].next=la[x];
		la[x]=xnt;
		xnt++;
		sid[xnt].lb=xnt-1;
		sid[xnt].to=x;
		sid[xnt].next=la[y];
		la[y]=xnt;
	}
	for(int i=1;i<=n;i++)
	{
		qq=i;
		memset(bd,0,sizeof bd);
		memset(str[sstr],0,sizeof str[sstr]);
		ser(i);
	}
	printf("%d",sstr-1);
	return 0;
}