计算机组成原理笔记
一、计算机系统概述
1.1 计算机的发展
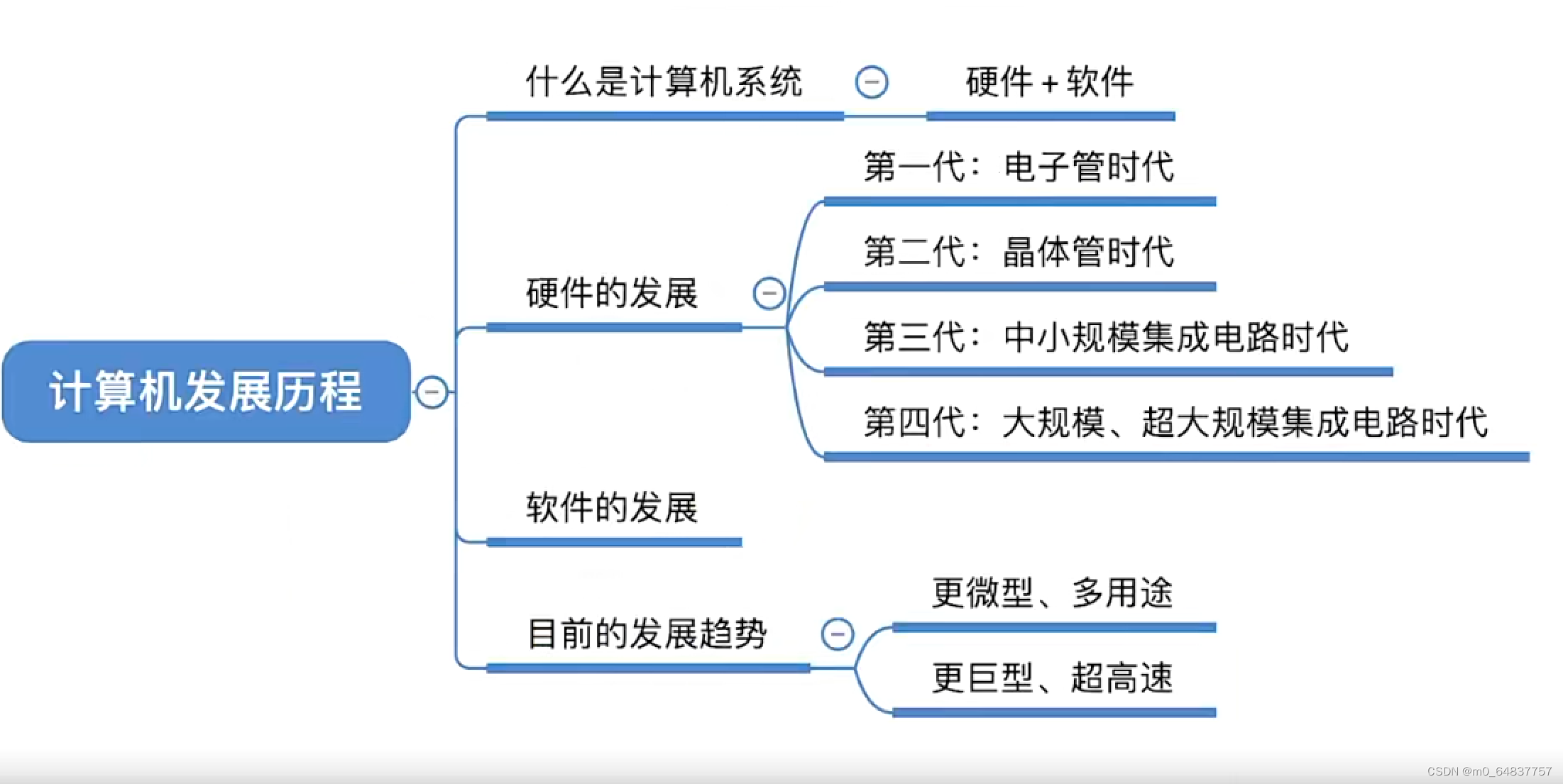

数据库管理系统–系统软件
数据库系统–应用软件
1.2 计算机硬件
1.2.1 计算机硬件的基本组成
早期的冯诺依曼机
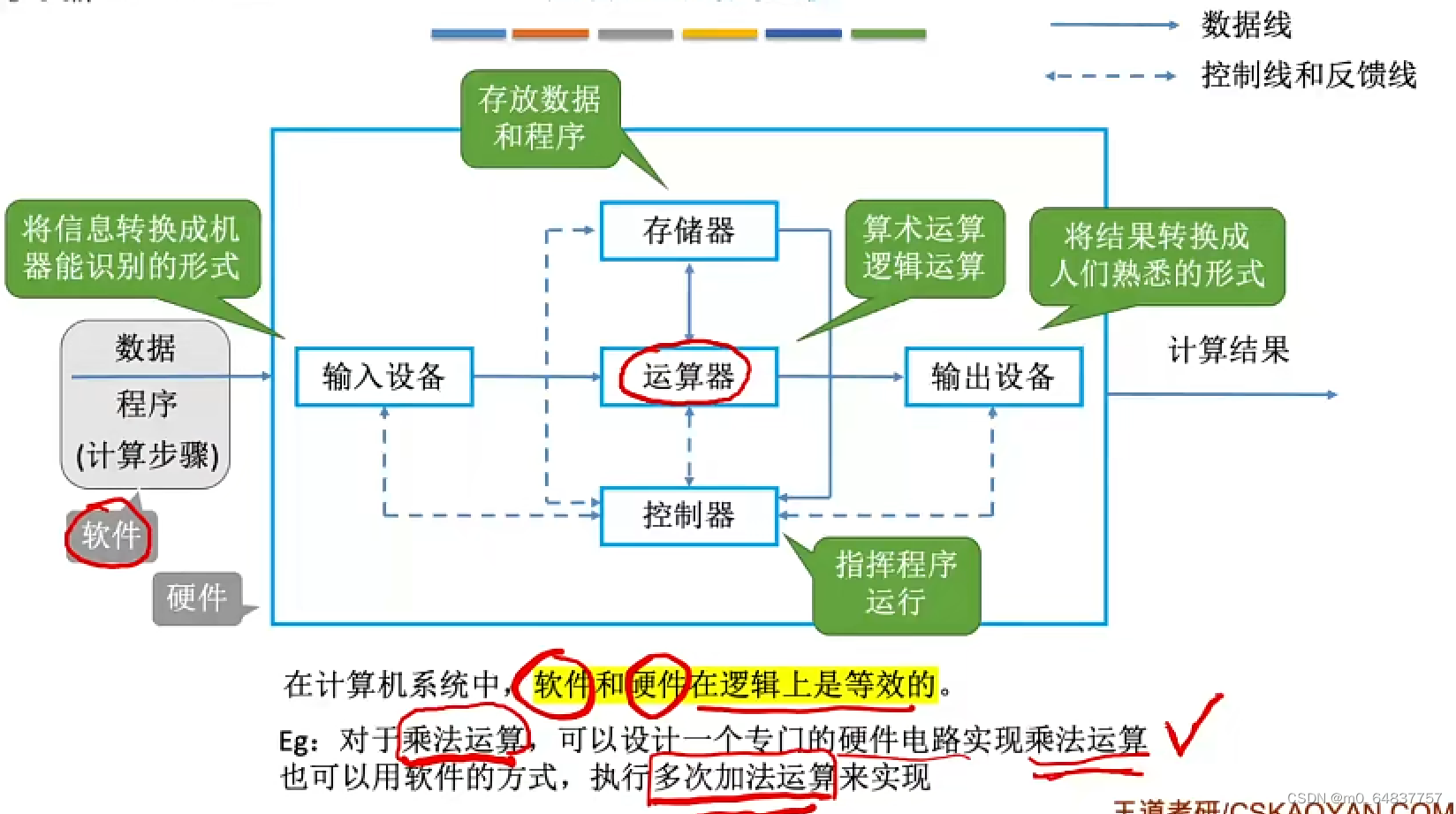
“存储程序”的概念是指将指令以二进制代码的形式事先输入计算机的主存储器,然后按其在存储器中的首地址执行程序的第一条指令,以后就按该程序的规定顺序执行其他指令,直到程序执行结束。 在这里插入图片描述
冯诺依曼计算机的特点
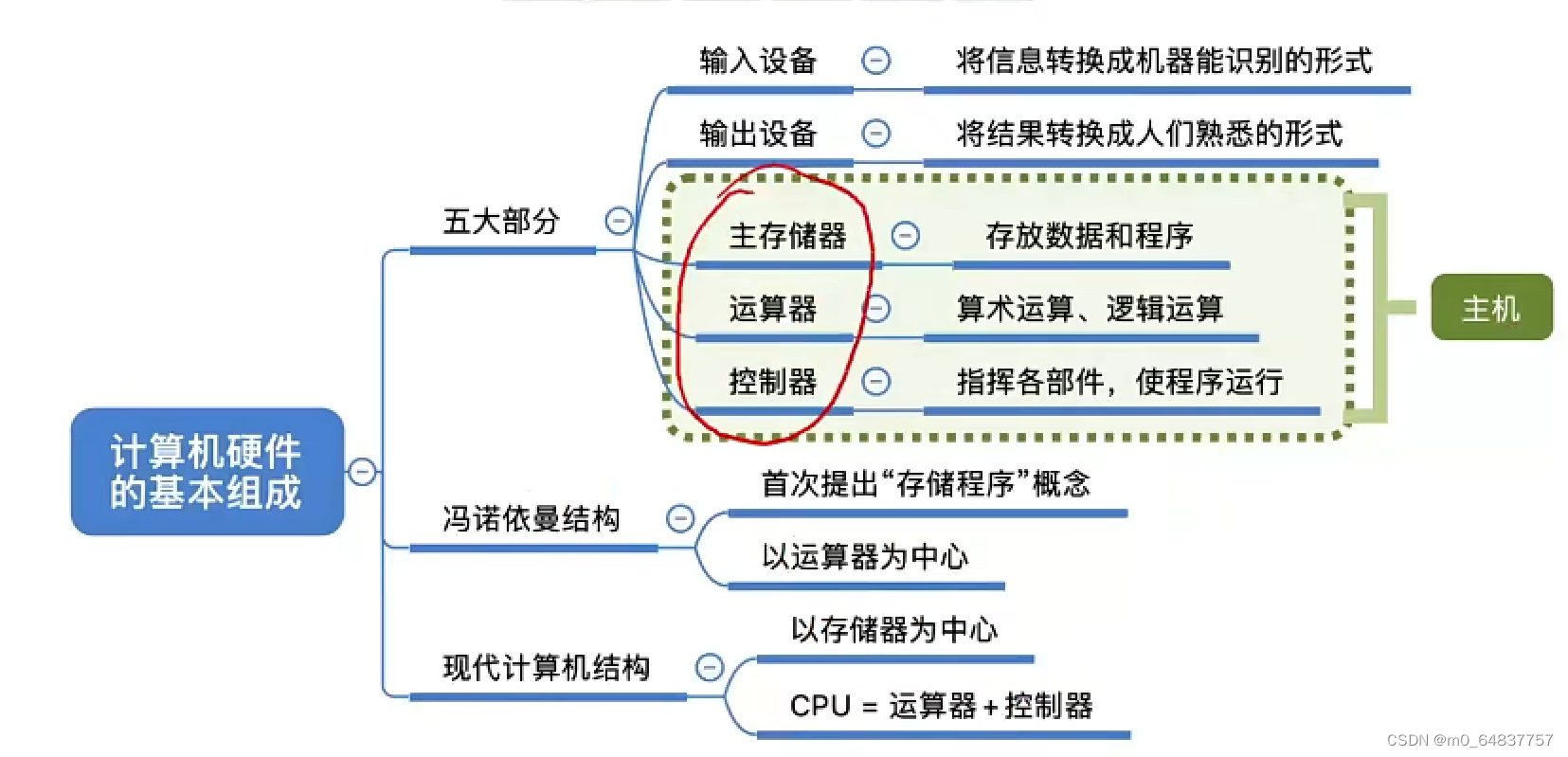
计算机由五大部件组成
指令和数据以同等地位存于存储器,可按地址访问(统一编址,指令和数据所在存储单元无差异)
指令和数据用二进制表示
指令由操作码和地址码组成
存储程序
以运算器为中心(输入输出设备与存储器之间的数据传送通过运算器完成)
数据驱动方式:
控制流驱动:指令–>数据
数据流驱动:数据–>指令
现代计算机的结构
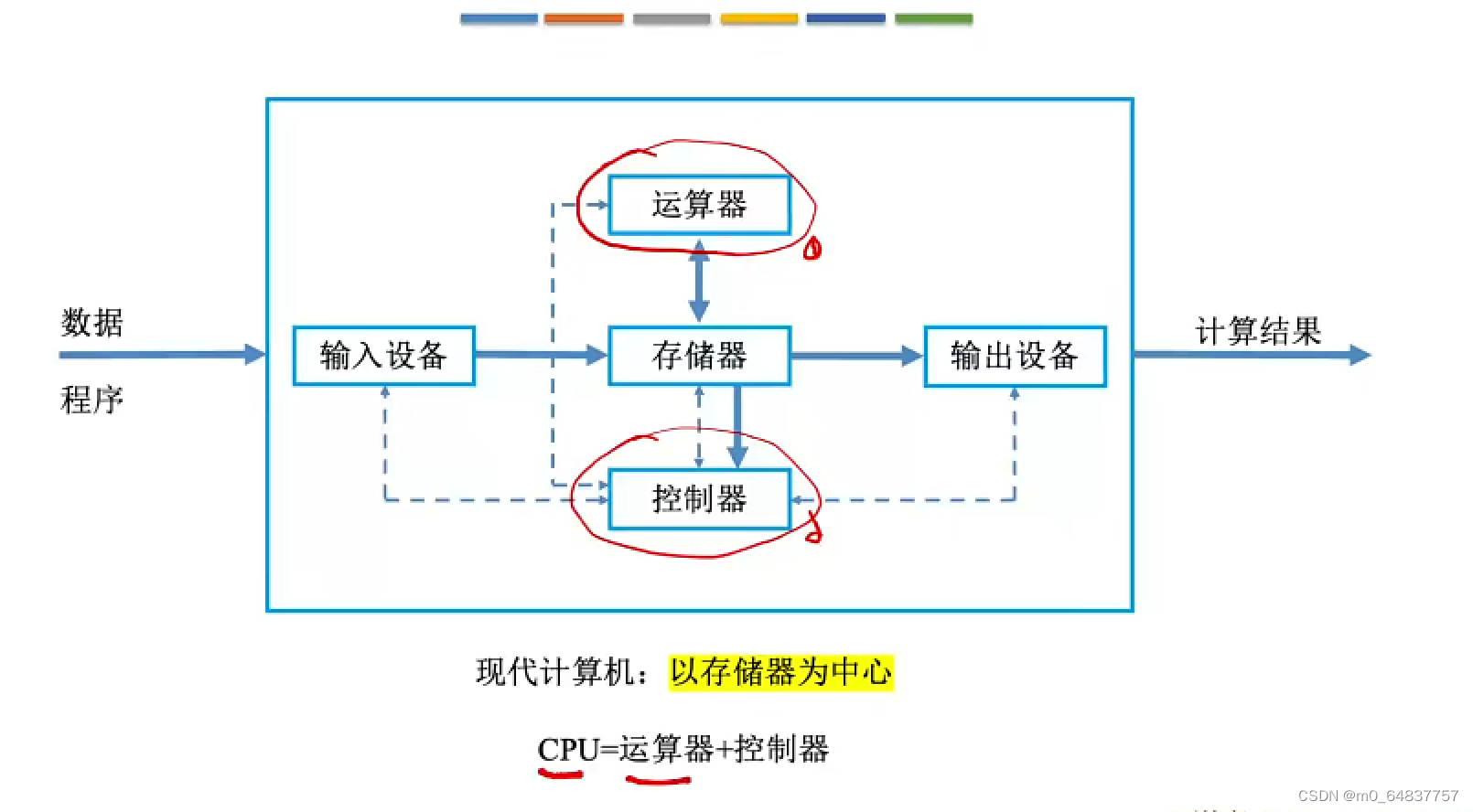
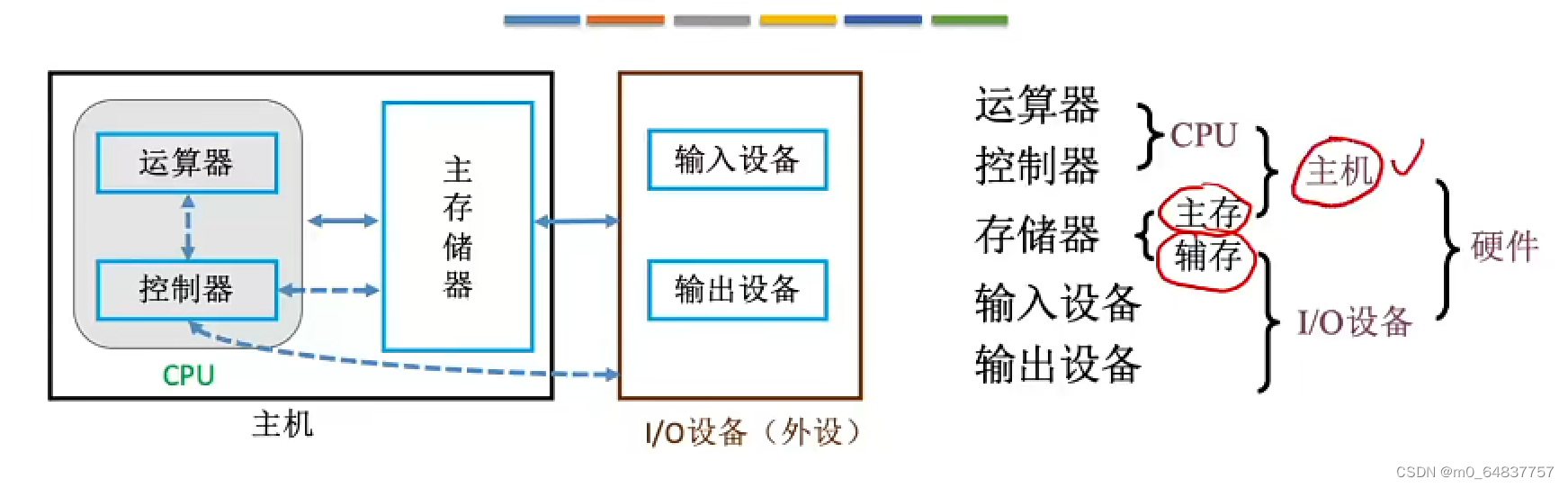
知识点回顾
1.2.2 各个硬件的工作原理
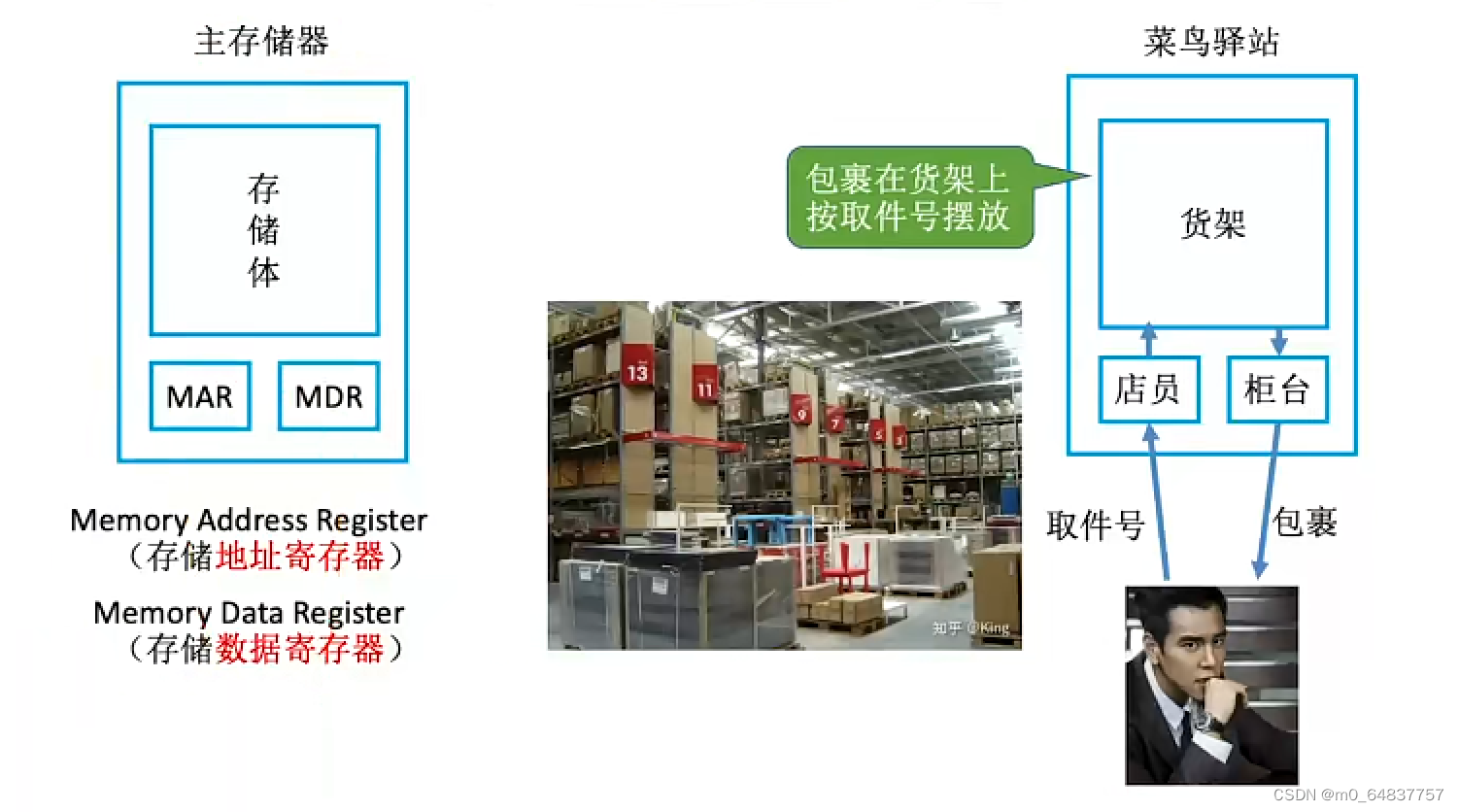
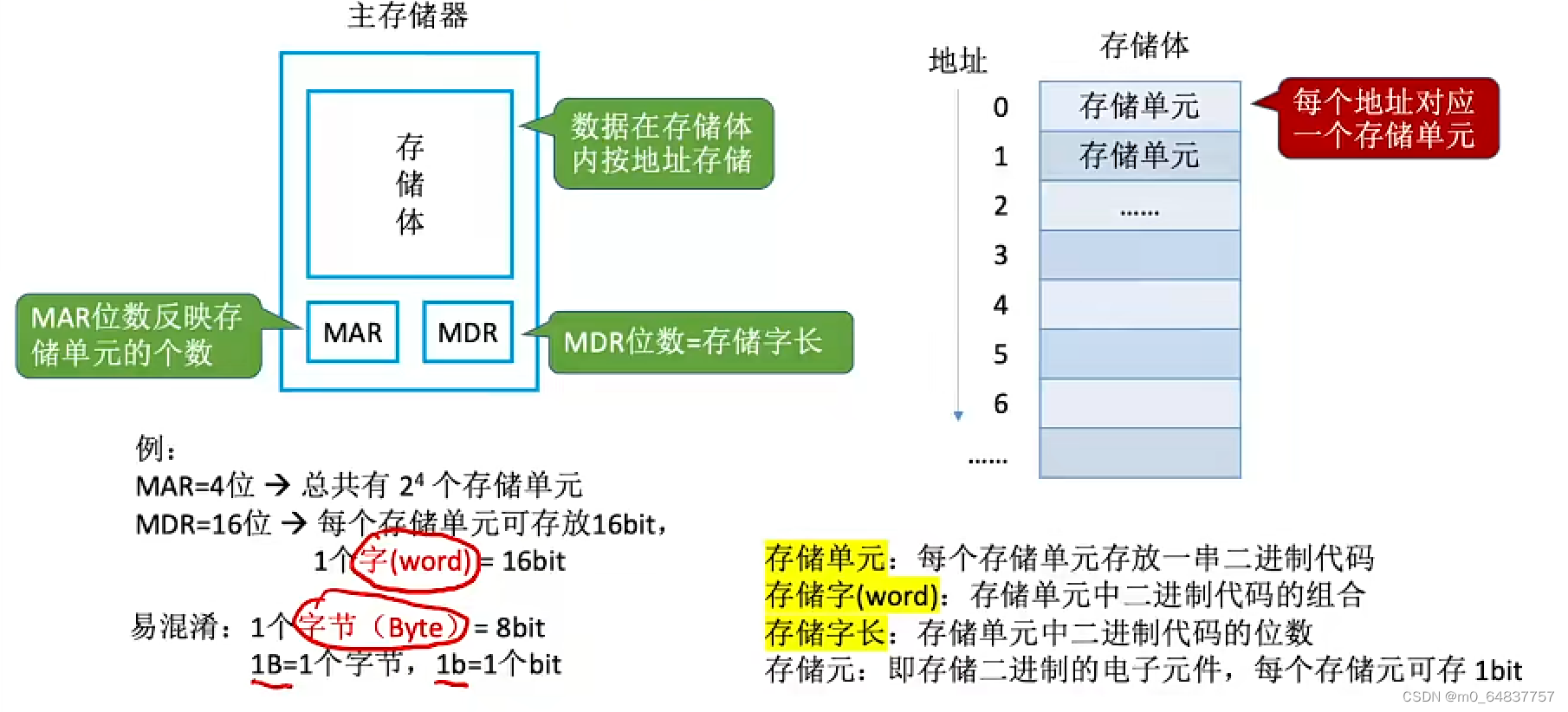
主存储器的基本组成
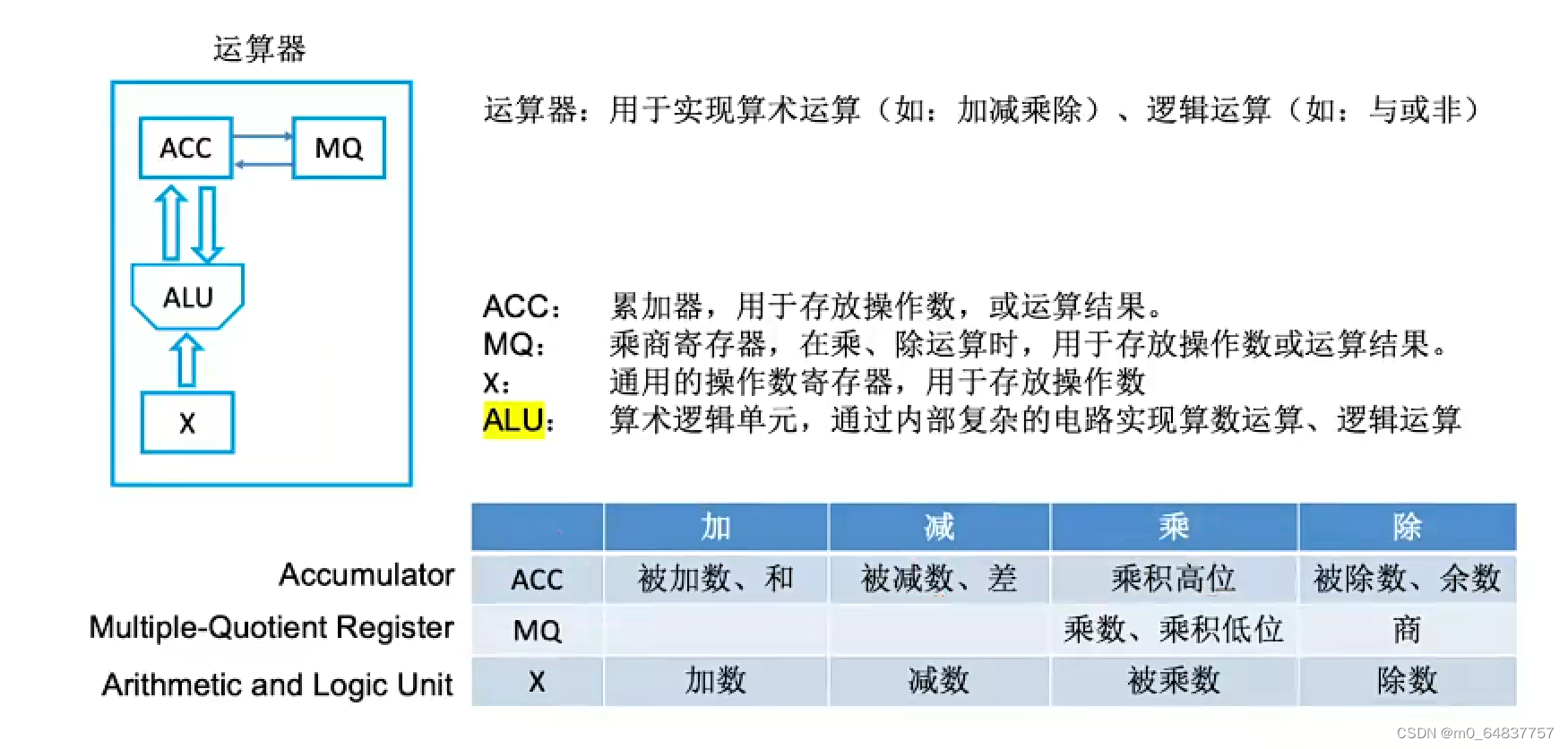
运算器的基本组成
控制器的基本组成

计算机的工作过程
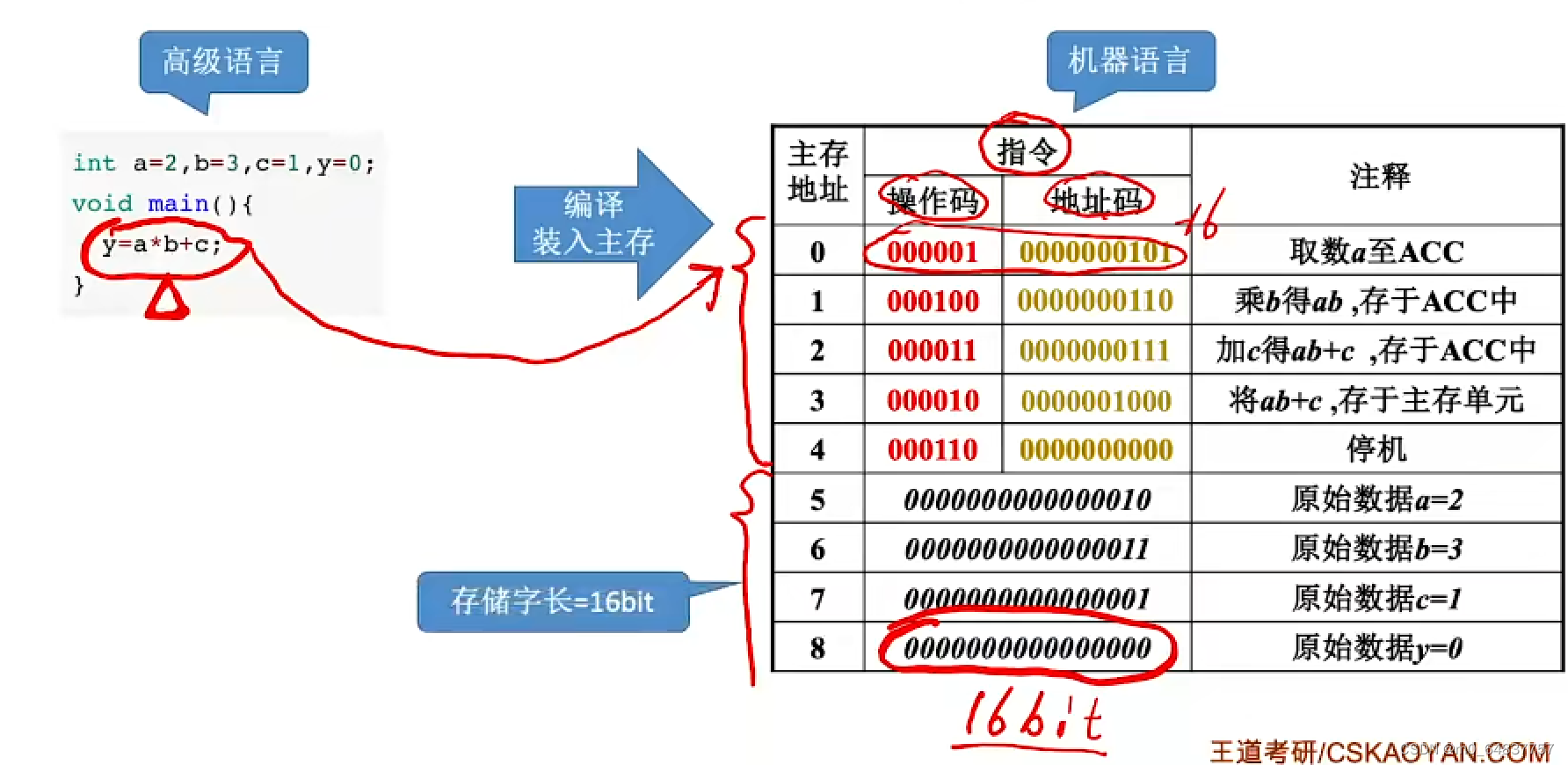
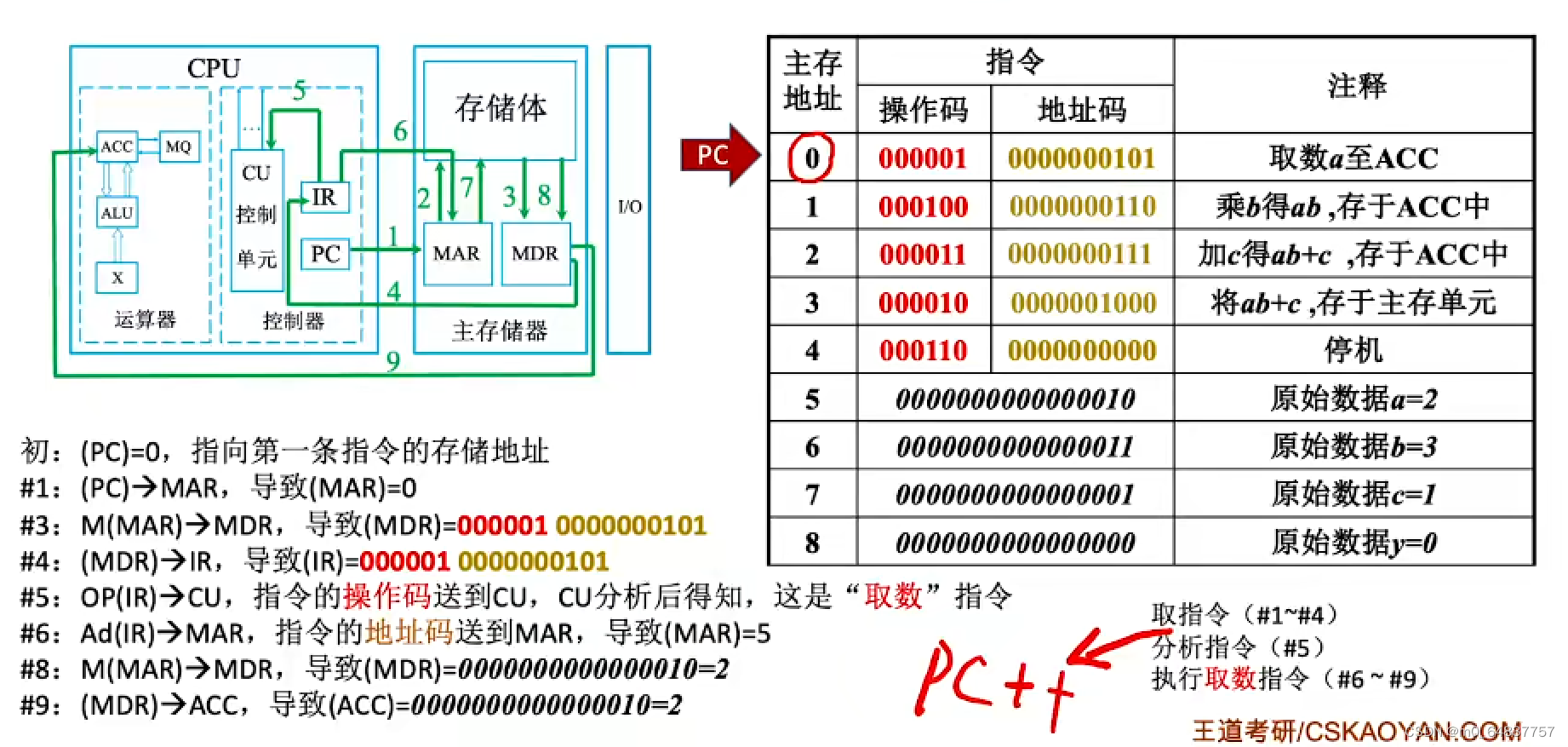
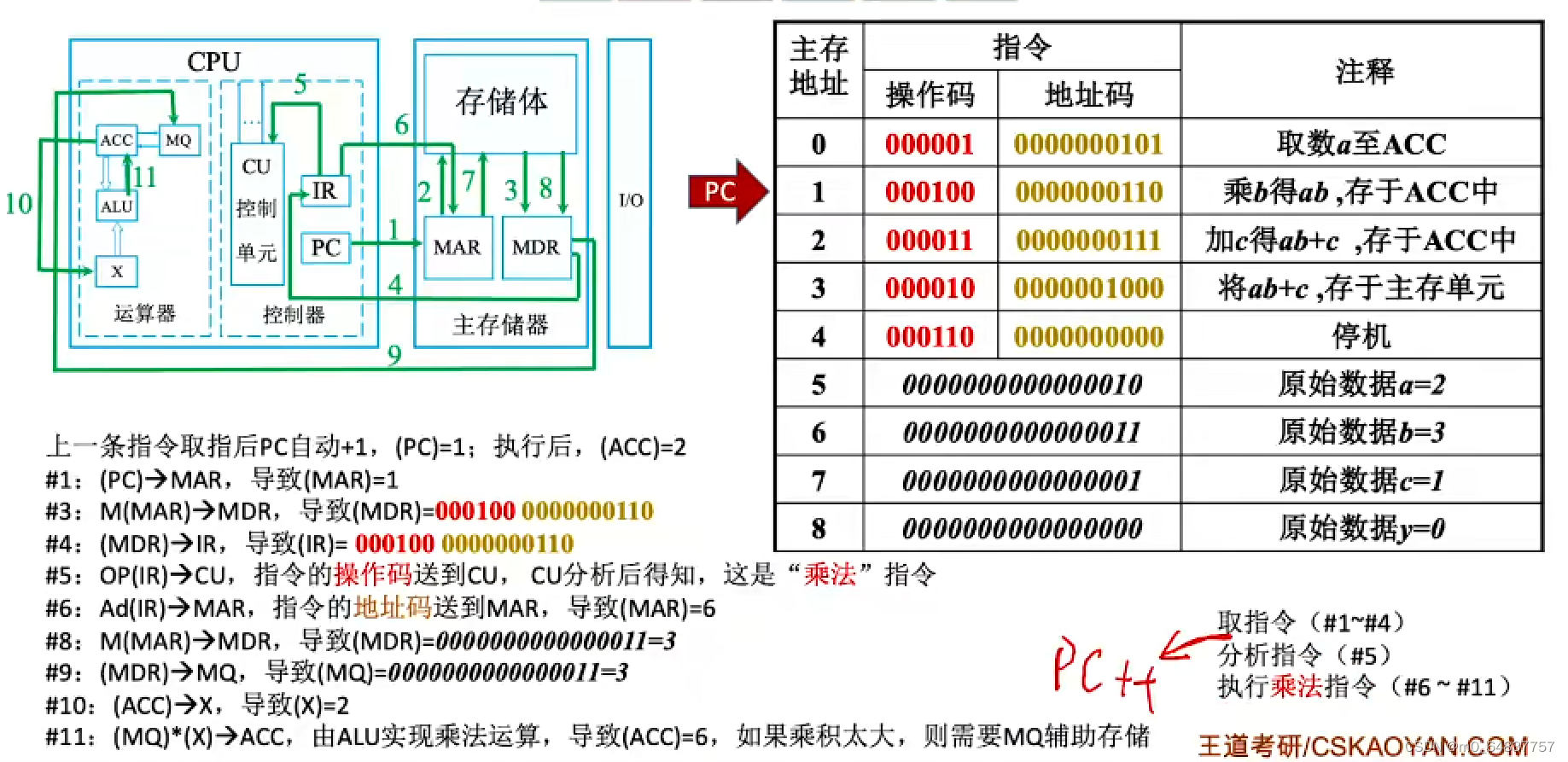
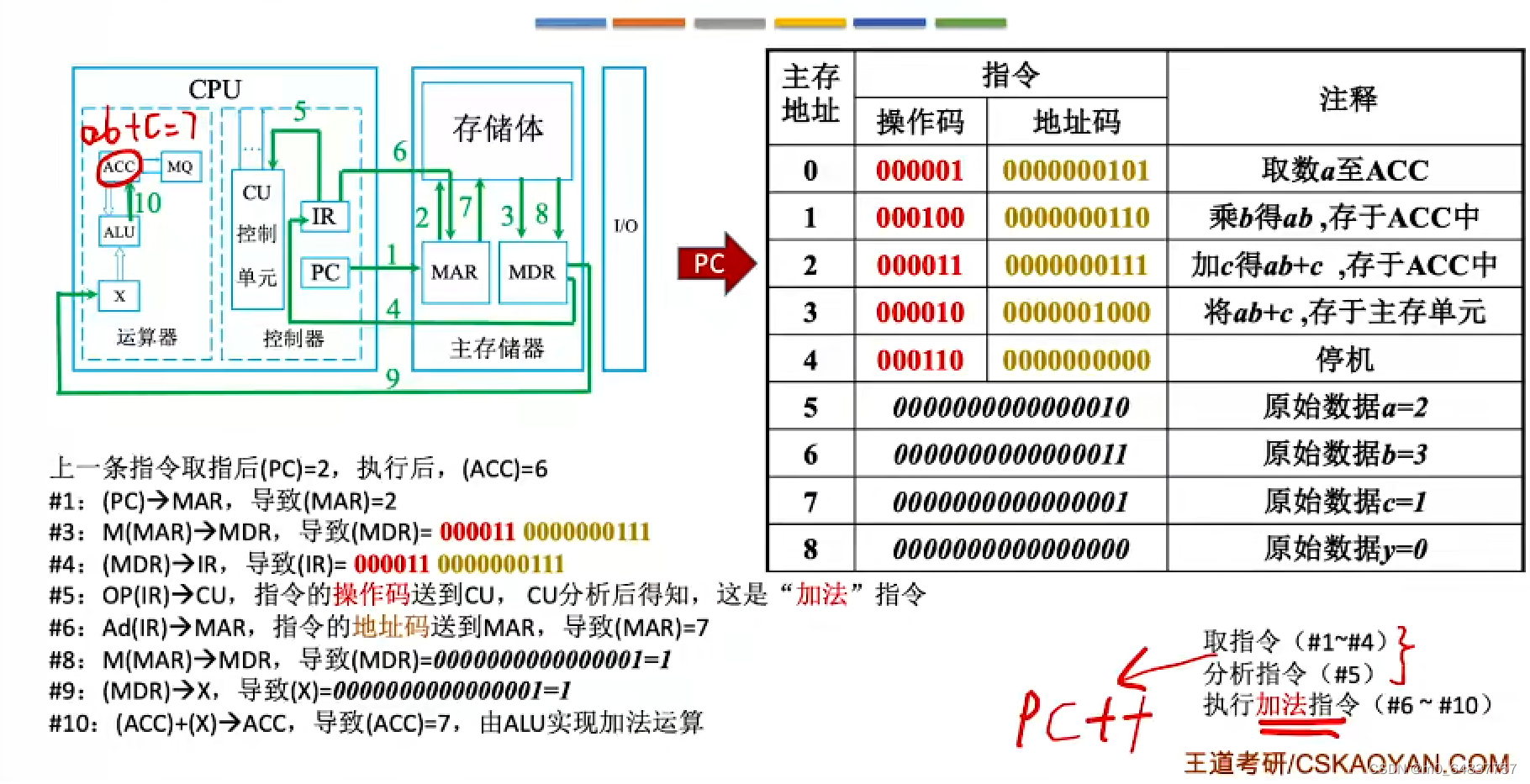
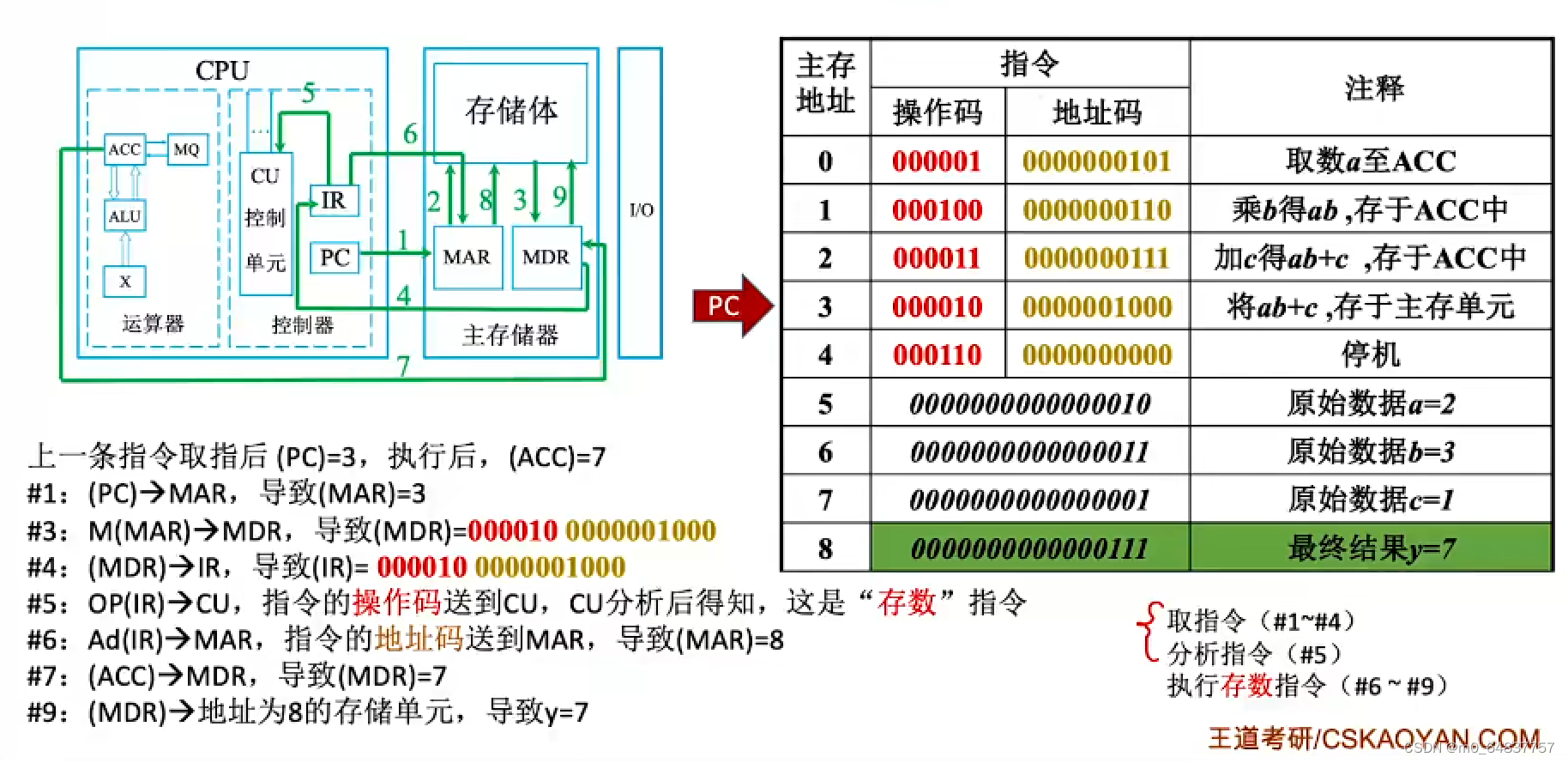
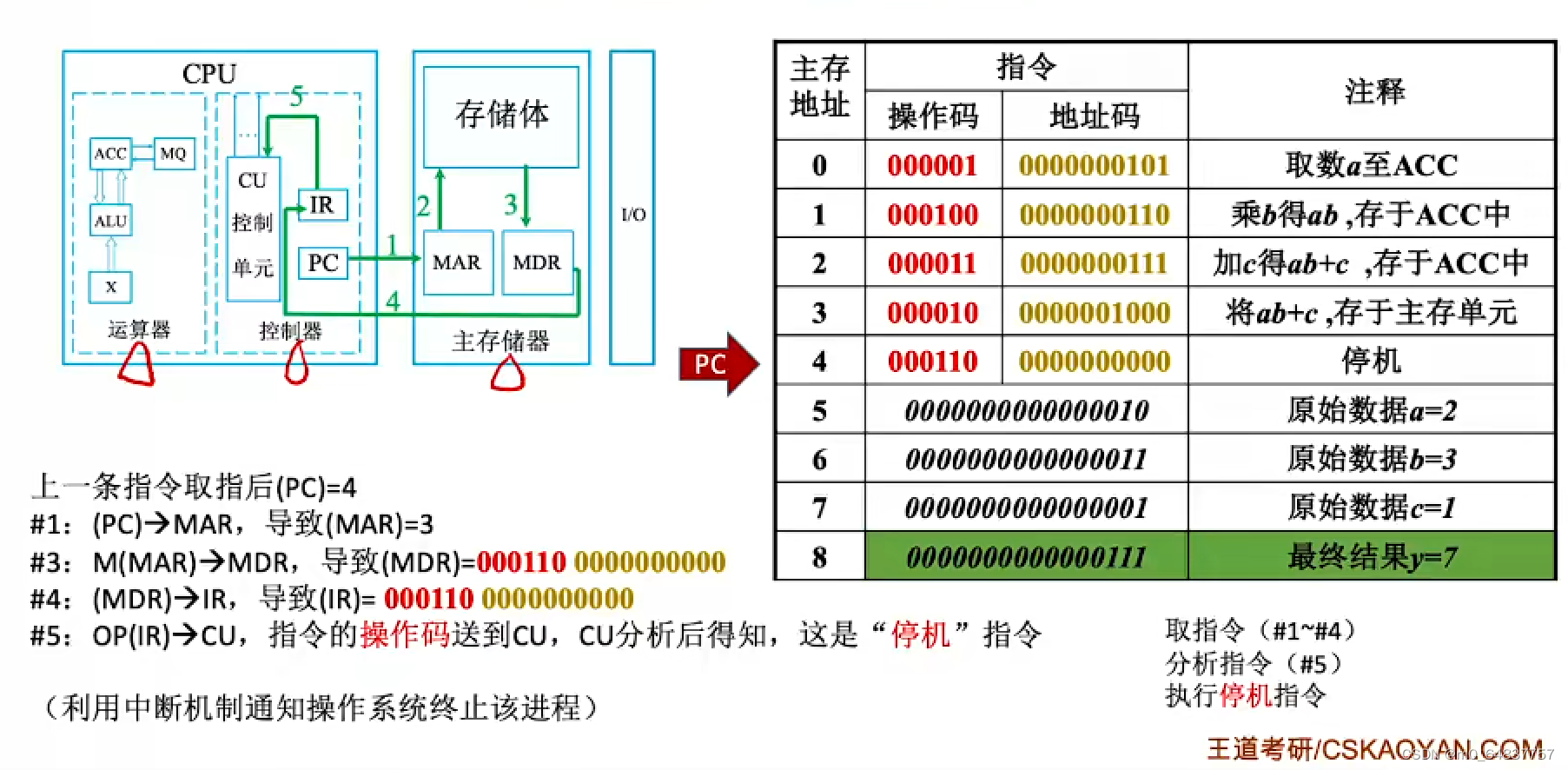
总结:
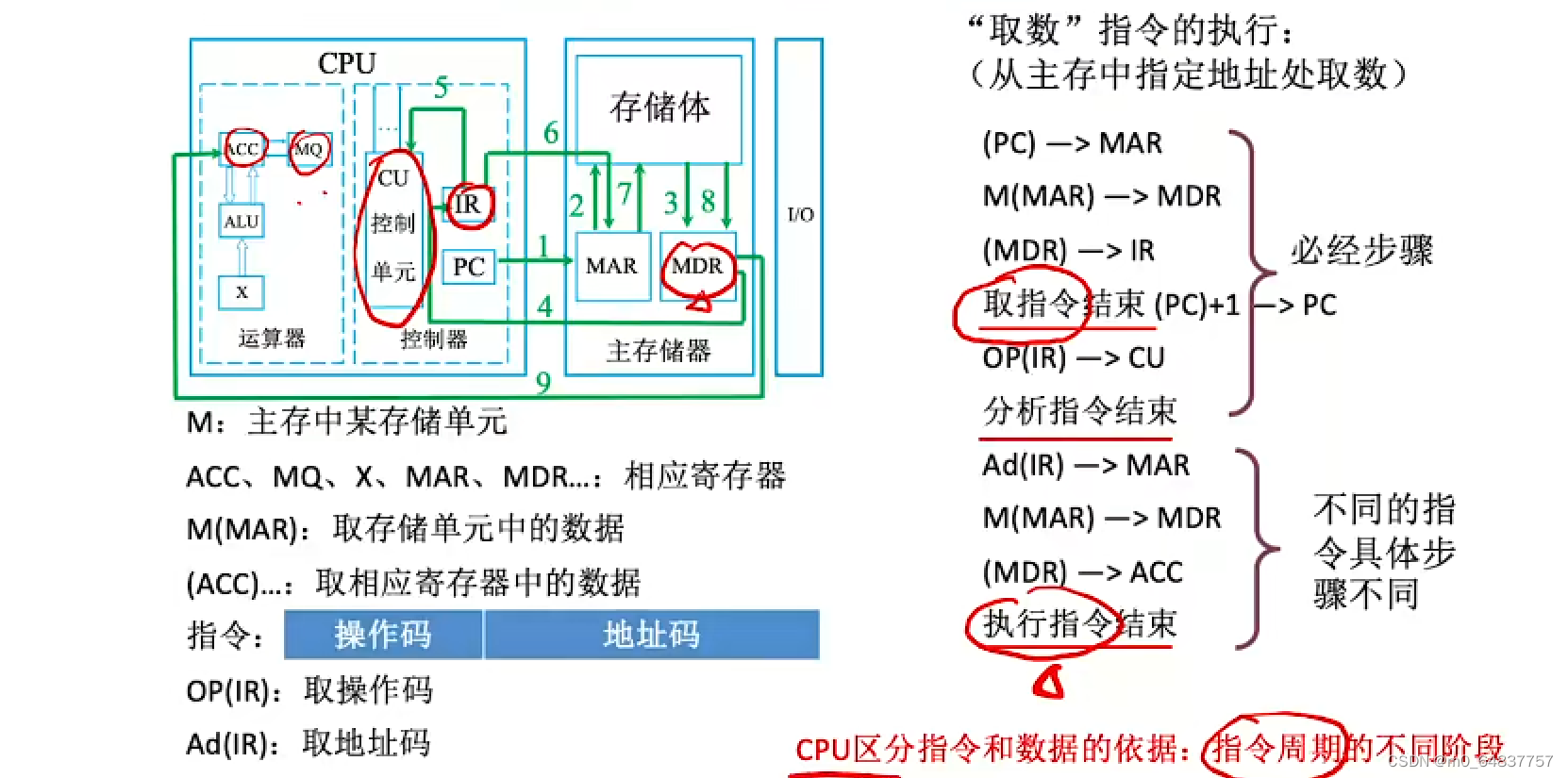
知识点回顾
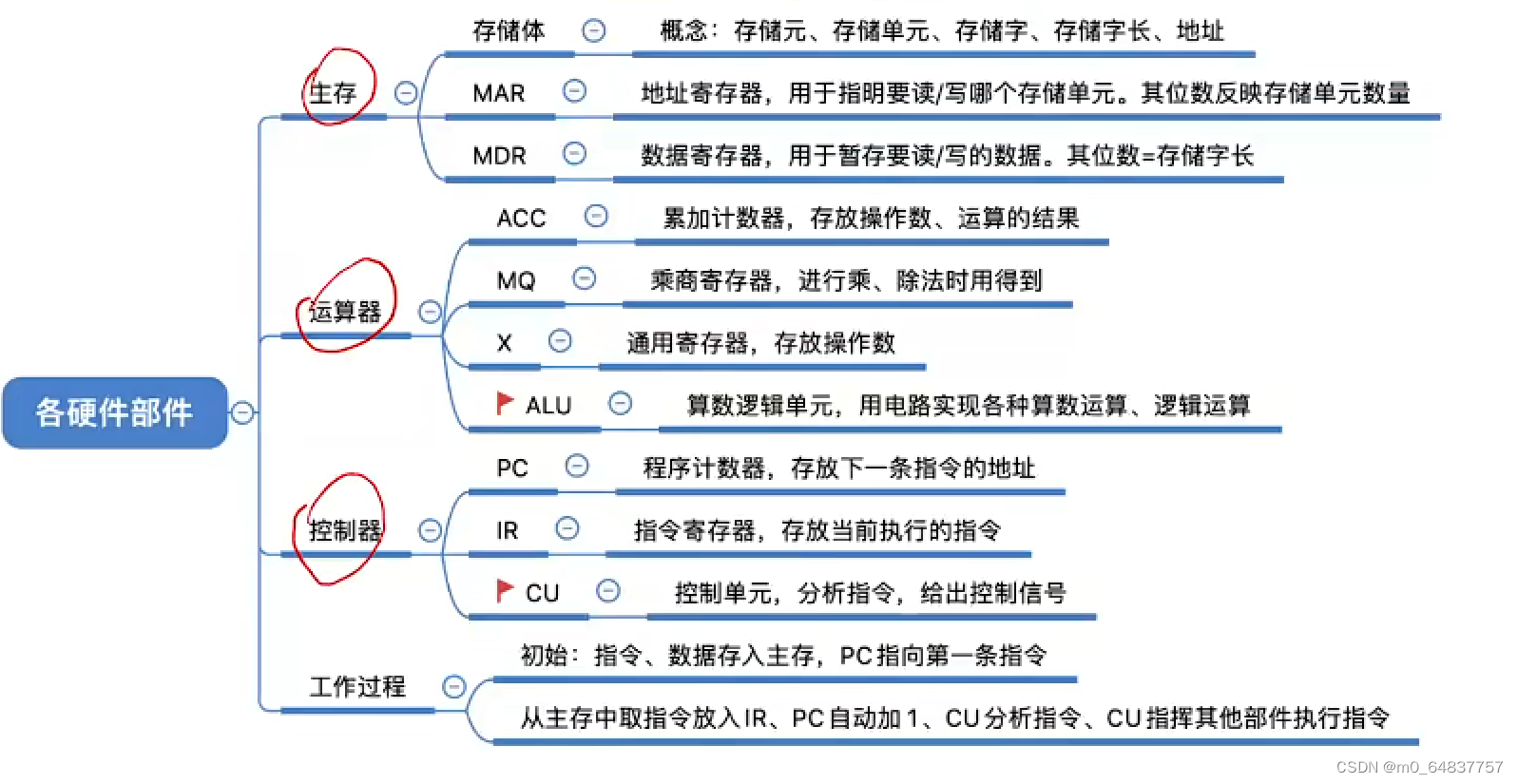
注:现在的计算机通常把MAR,MDR也集成在CPU内
1.2.3 计算机系统的层次结构
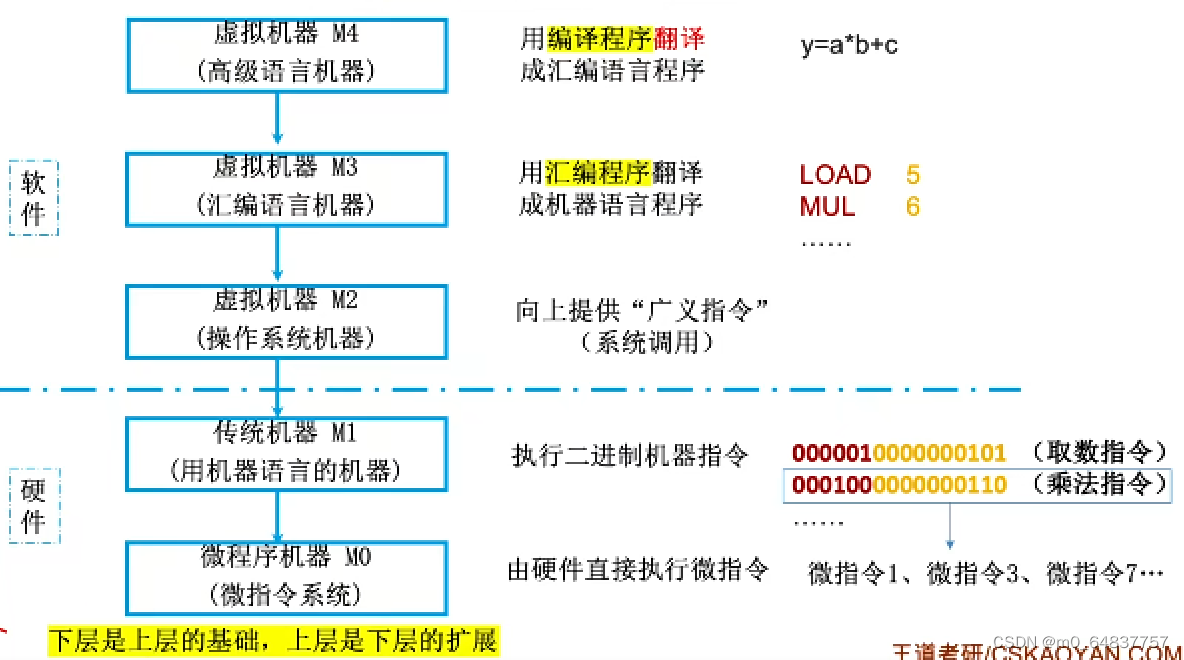
汇编语言指令和机器语言指令一一对应
LOAD: 取数操作 ,MUL: 乘法操作
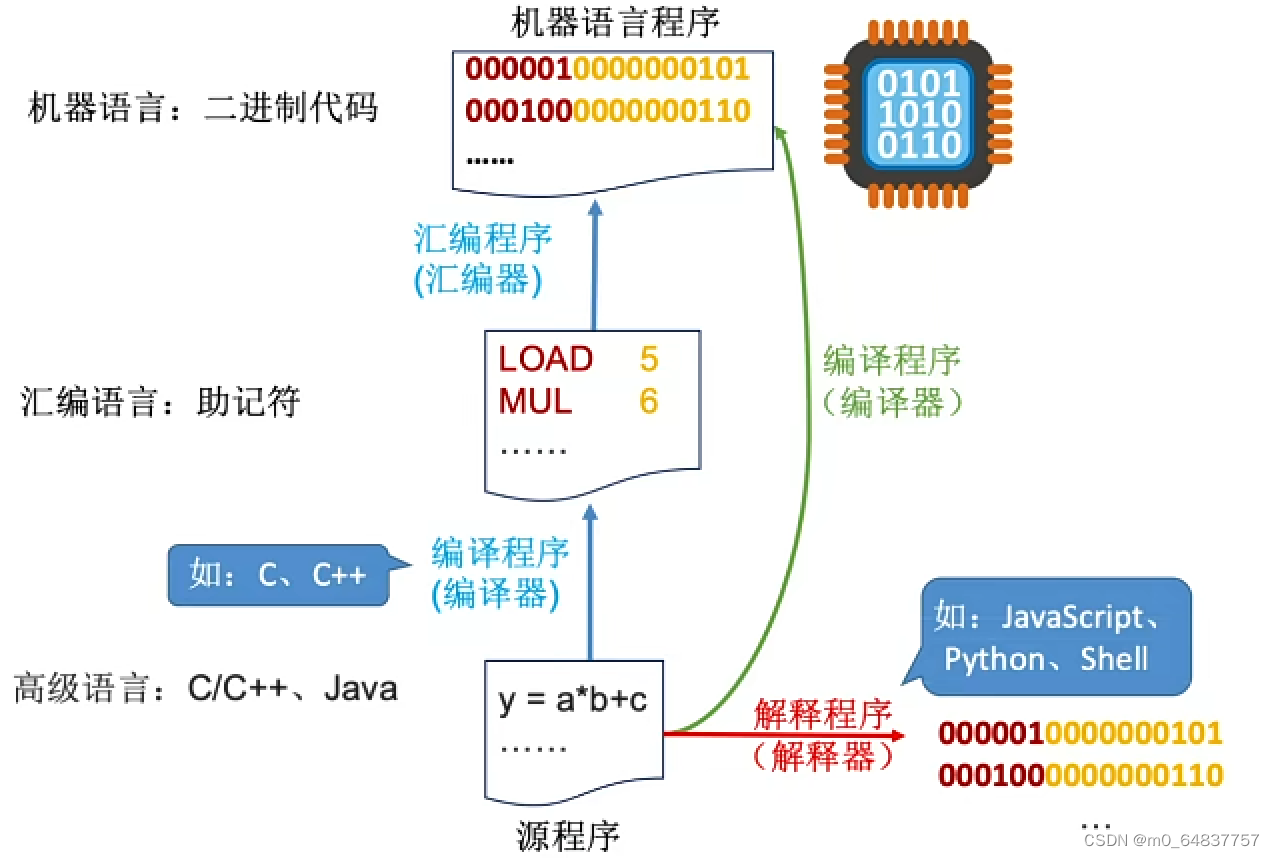
编译程序:将高级语言编写的源程序全部语句一次全部翻译成机器语言程序,而后在执行机器语言程序(只需翻译一次)。 例如:使用我们使用C语言写的程序,经过编译和汇编之后,最终形成.exe文件,该.exe文件是用机器语言描述的程序,每次运行这个程序,只需加载.exe文件。
解释程序:将源程序的一条语句翻译成对应于机器语言的语句,并立即执行。紧接着在翻译下一句(每一次都要翻译)。 编译型语言执行效率较解释型语言高。 注:编译、汇编、解释程序,可统称为“翻译程序”。
计算机体系结构:机器语言程序员所见到的计算机系统的属性概念性的结构与功能特性(指令系统、数据类型、寻址技术、I/O机理)
如何设计硬件与软件之间的接口。
计算机组成原理:实现计算机体系结构所体现的属性,对程序员“透明”(具体指令的实现)
如何用硬件实现所定义的接口。
“透明”:看不见
“公开透明”:看得见

知识点回顾
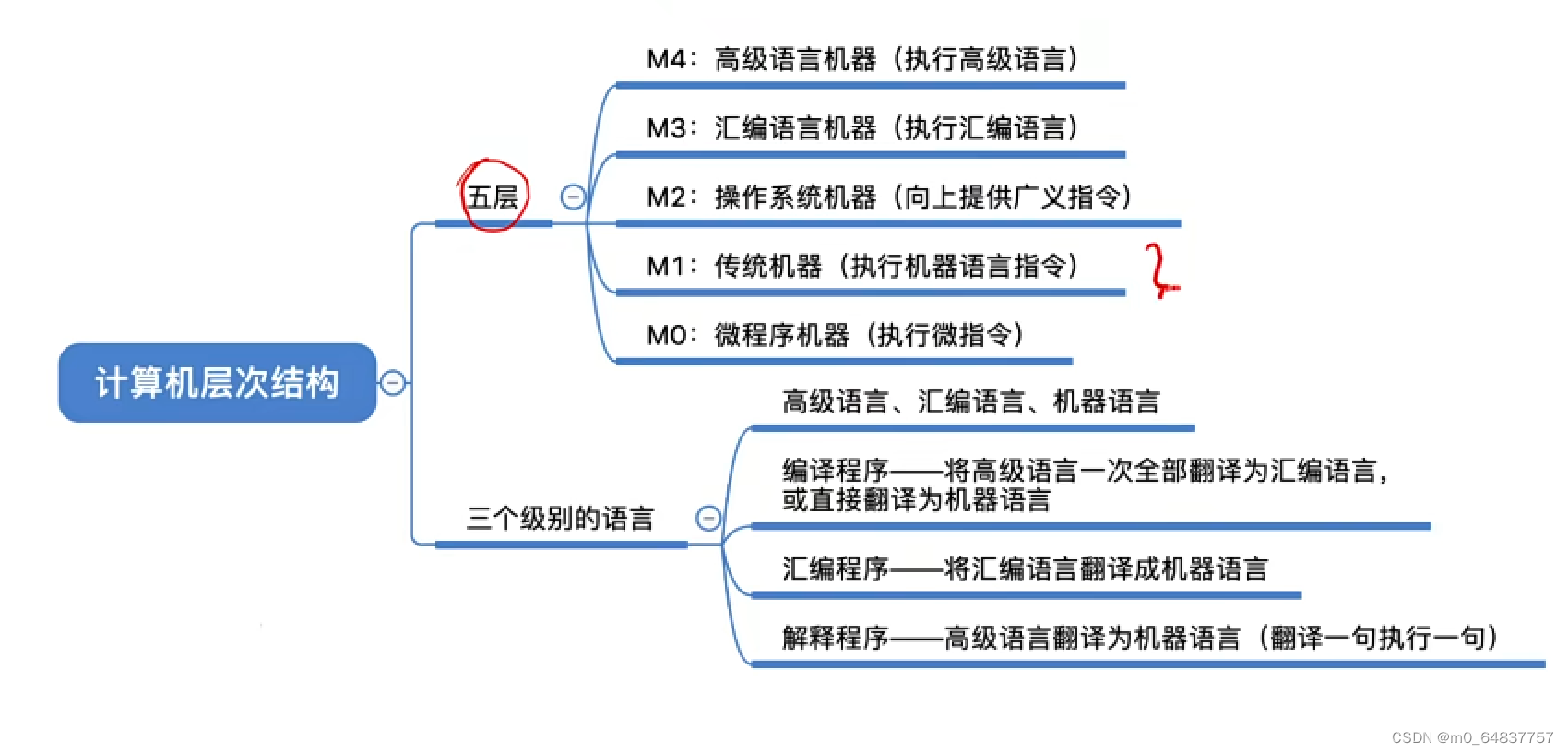
1.3 计算机性能指标
机器字长:能够直接处理的二进制数据的位数
指令字长:一个指令中包含的二进制代码的位数
存储字长:一个存储单元二进制数据的位数
1.3.1 存储器性能指标
MAR位数反应存储单元的个数(最后支持多少个)
MDR位数=存储字长=每个存储单元的大小
总容量=存储单元个数×存储字长 bit =存储单元个数×存储字长/8 Byte
Eg:MAR为32位,MDR为8位
总容量=2^32×8 bit=4GB
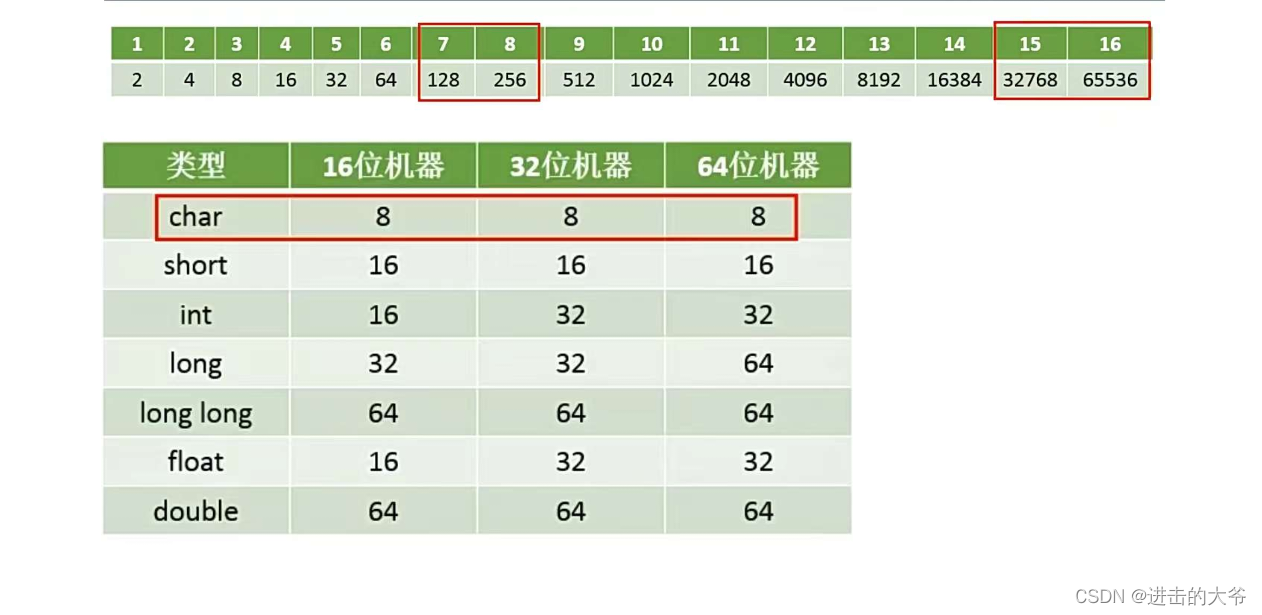
n个2进制位能表示多少种不同的状态

2^10:K
2^20:M
2^30:G
2^40:T
1.3.2 CPU性能指标
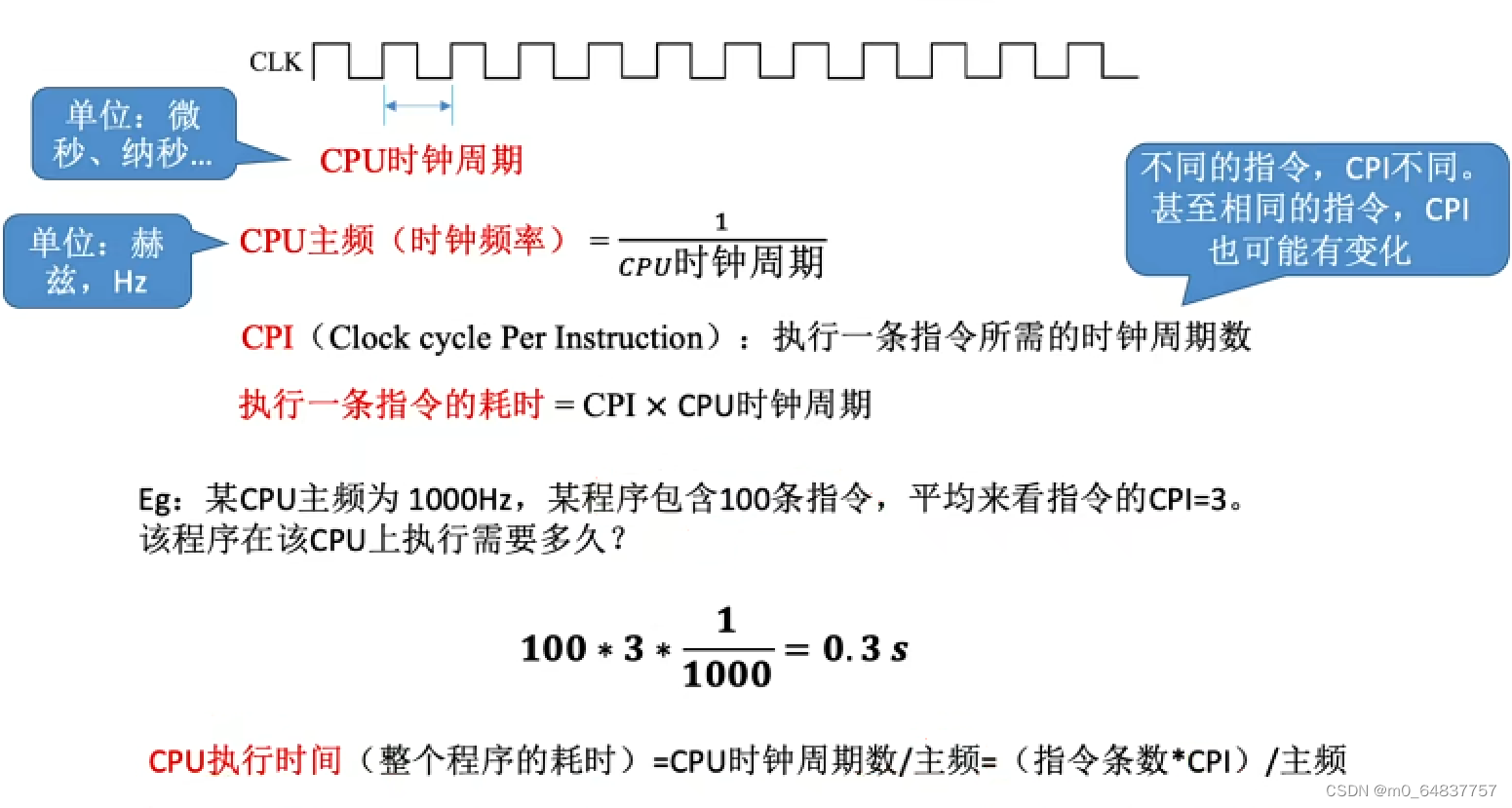

注:公式中主频的值反映的是:每秒钟会出现多少个时钟周期。

注:注意与存储器的容量或者文件的大小中的K、M、G、T的区别
1.3.3 系统整体的性能指标
数据通路带宽:数据总线一次所能并行传送信息的位数(各硬件部件通过数据总线传输数据)
吞吐量:指系统在单位时间内处理请求的数量。他取决于信息能多快地输入内存,CPU能多快地取指令,数据能多快地从内存取出或存入,以及所得结果能多快地从内存送给一台外部设备。这些步骤中的每一步都关系到主存,因此,系统吞吐量主要取决于主存的存取周期。
响应时间:指从用户向计算发送一个请求,到系统对该请求做出响应并获得它所需要的结果的等待时间。通常包括CPU时间(运行一个程序所花费的时间)与等待时间(用于磁盘访问、存储器访问、I/O操作、操作系统开销时间)。
动态测试:基准程序(跑分软件)是用来测量计算机处理速度的一种实用程序,以便于被测量的计算机性能可以与运行相同程序的其他计算机性能进行比较。
思考:
1、主频高的CPU一定比主频低的CPU快吗?
答:不一定,如两个CPU,A的主频为2GHz,平均CPI=10,一秒钟可以执行0.2G条指令;B的主频为1GHz,平均CPI=1,一秒钟可以执行1G条指令。
2、若A、B两个CPU的平均CPI相同,那么A一定更快吗?
答:不一定,还要看指令系统,如A不支持乘法指令,只能用多次加法实现乘法;而B支持乘法指令。
3、基准程序执行的越快说明机器性能越好吗?
答:基准程序中的语句存在频度差异,运行结果也不能完全说明问题。
知识点回顾
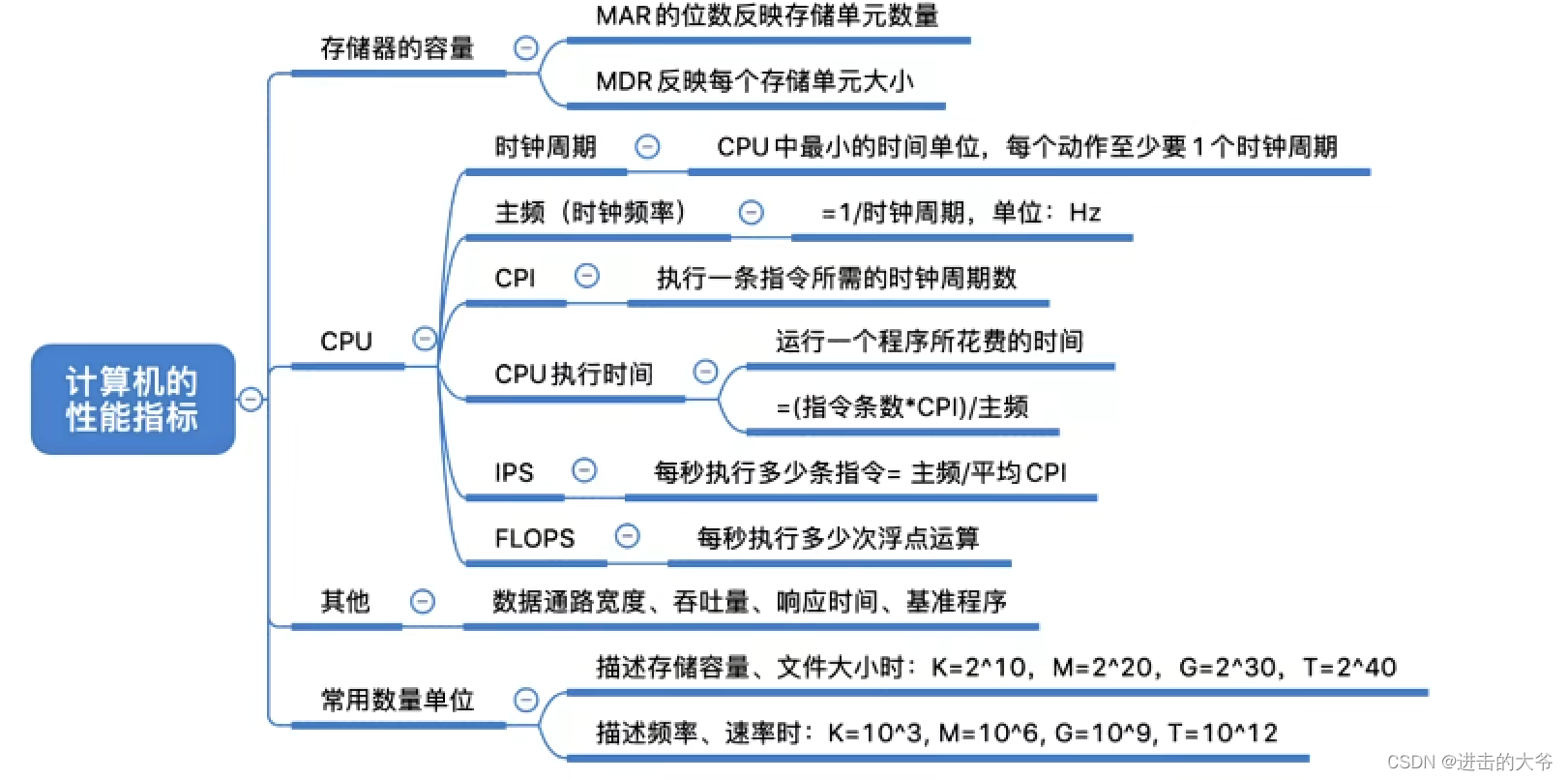
存储器的容量:衡量计算机的存储容量
机器字长:衡量计算机并行处理的能力
数据通路带宽:衡量计算机在功能部件之间传送数据的能力
二、数据的表示和运算
2.1
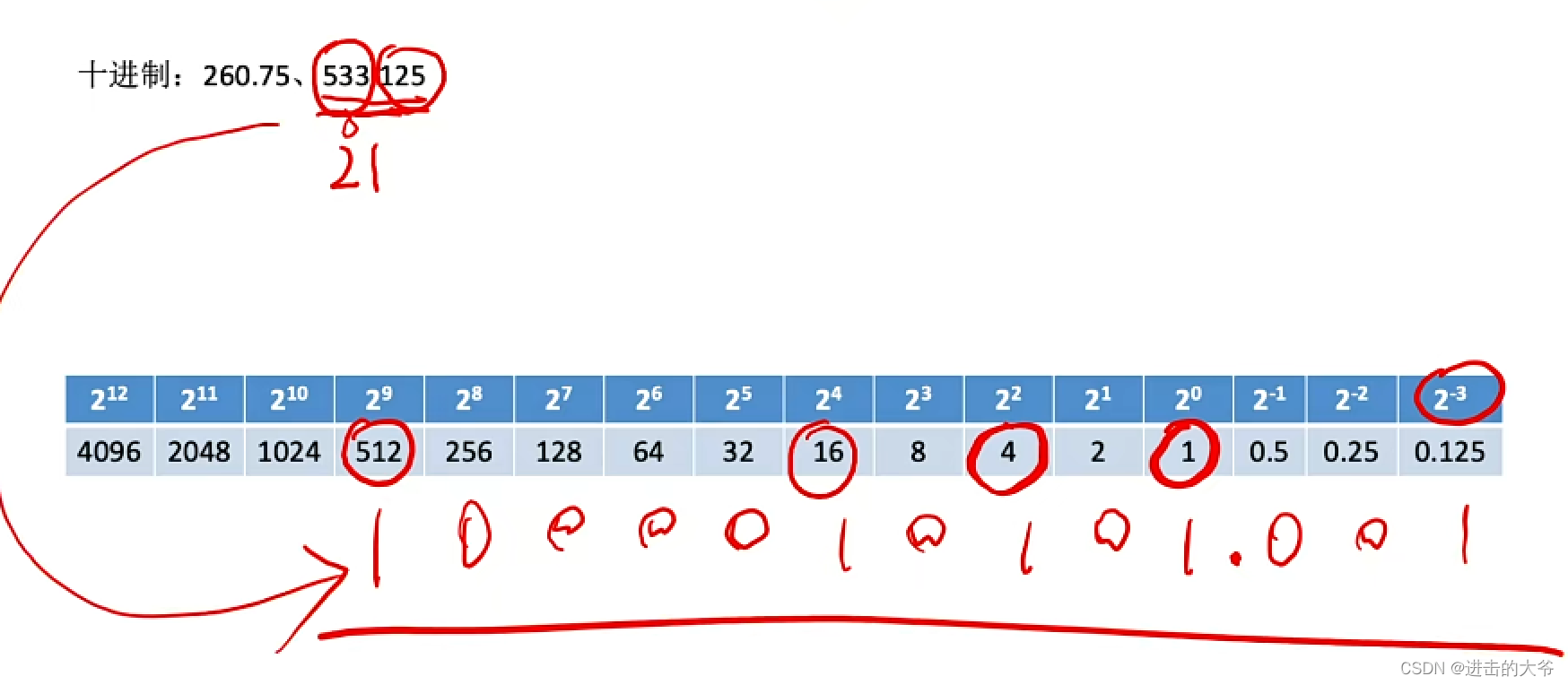
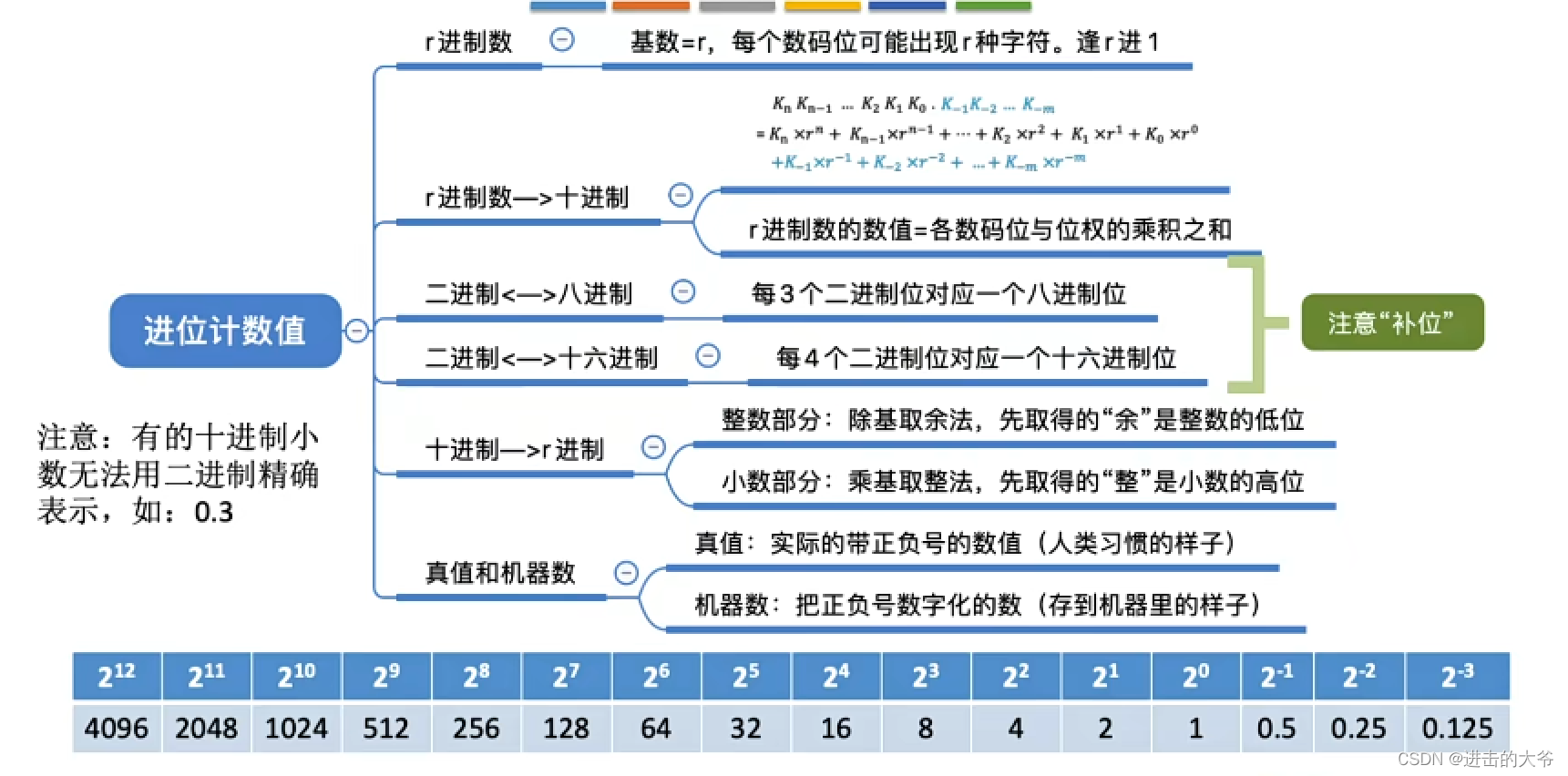
2.1.1 进位计数制
任意进制转换成十进制

二进制<=>八进制、十六进制

各种进制的常见书写方式

十进制转换成任意进制


真值和机器数

知识回顾与重要考点
2.1.3 无符号整数的表示和运算
无符号整数,即“自然数”,0、1、2、3、4、5…
C语言中的无符号整数:
unsigned short a=1; //无符号整数 (短整型 2B) unsigned int b=2; //无符号整数 (整型 4B)
无符号整数的表示
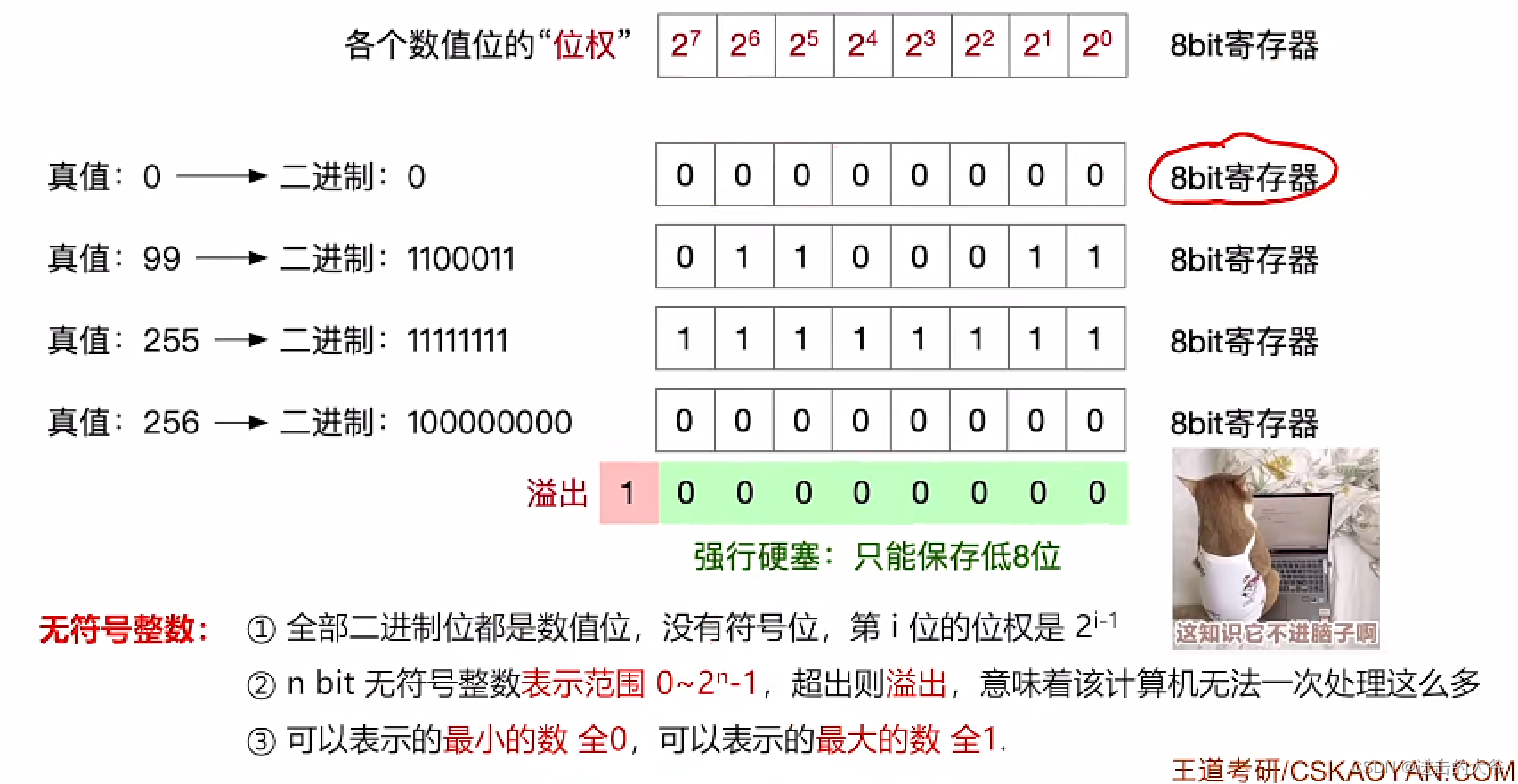
无符号整数的加法运算

无符号整数的减法运算
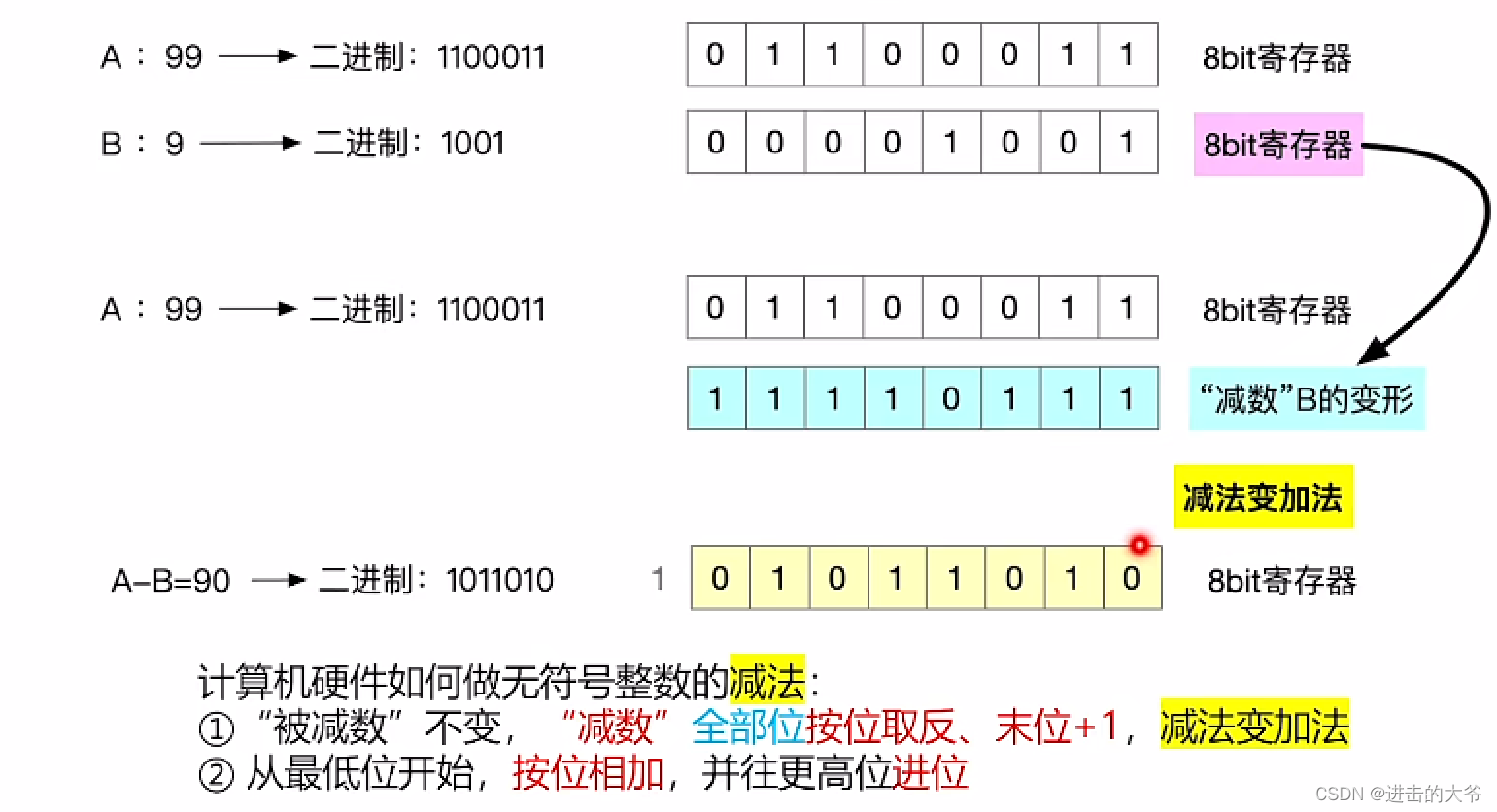
2.1.4 带符号整数的表示和运算_原反补
带符号整数,即“整数”,-2、-1、0、1、2、3、4、5…
C语言中的带符号整数:
short a=1; //带符号整数 (短整型 2B) int b=-2; //带符号整数 (整型 4B)
原码表示
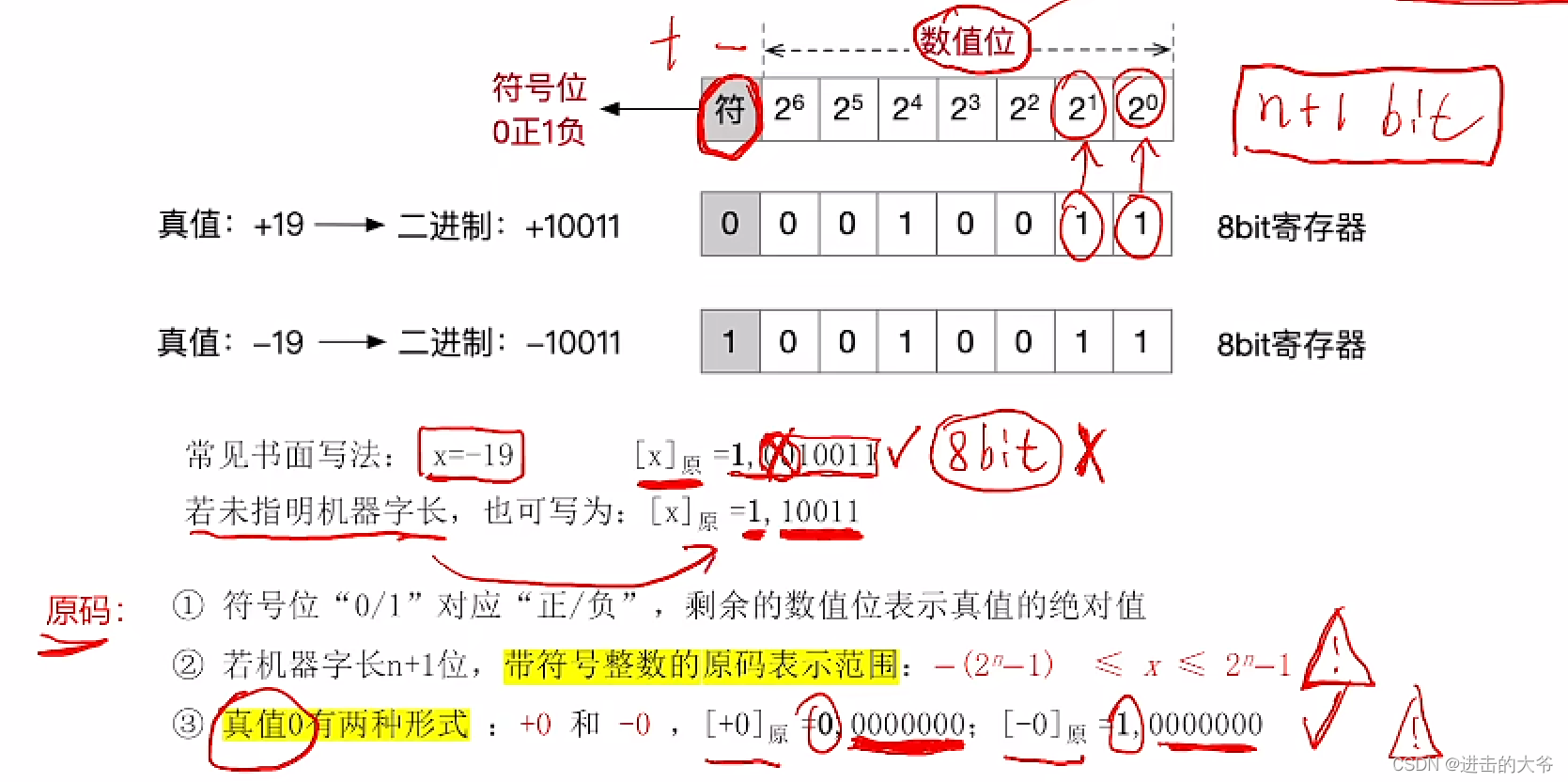
原码的缺点:符号位不能参与运算,需要设计复杂的硬件电路才能处理
用补码表示真值–符号位可以参与运算
原码、反码、补码的转换(计算)
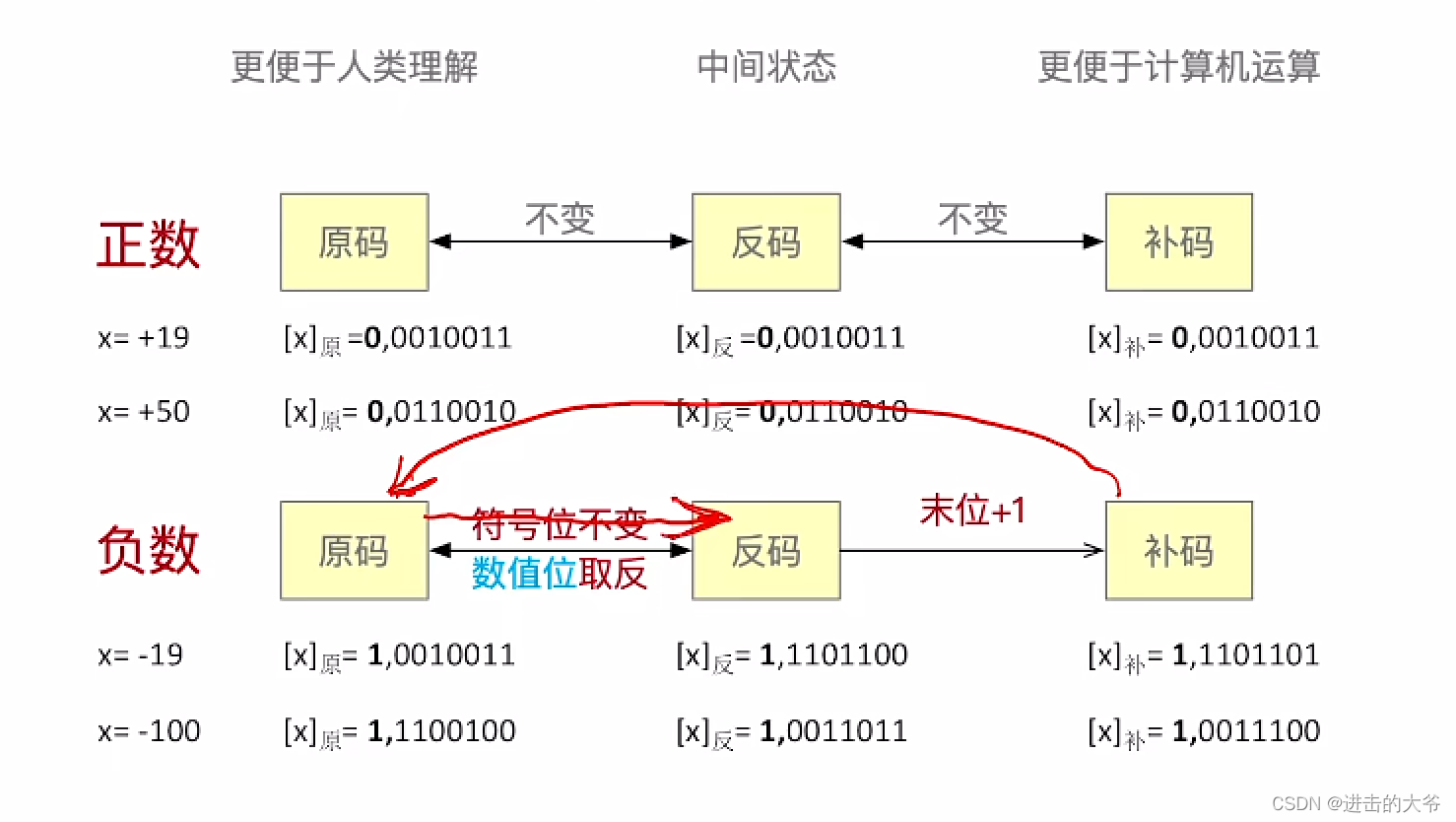
原码、反码、补码快速转换技巧(手算)
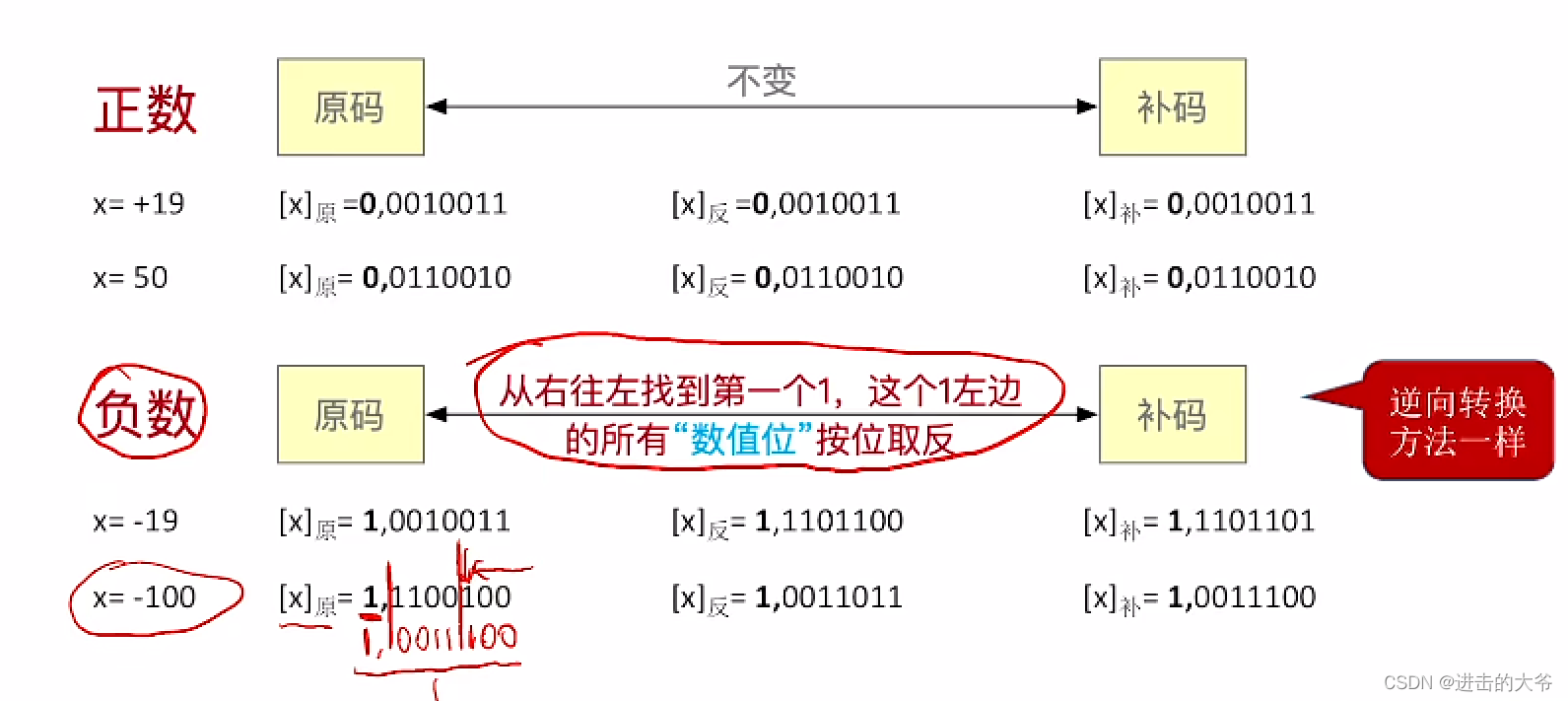
补码的加法运算(例1)
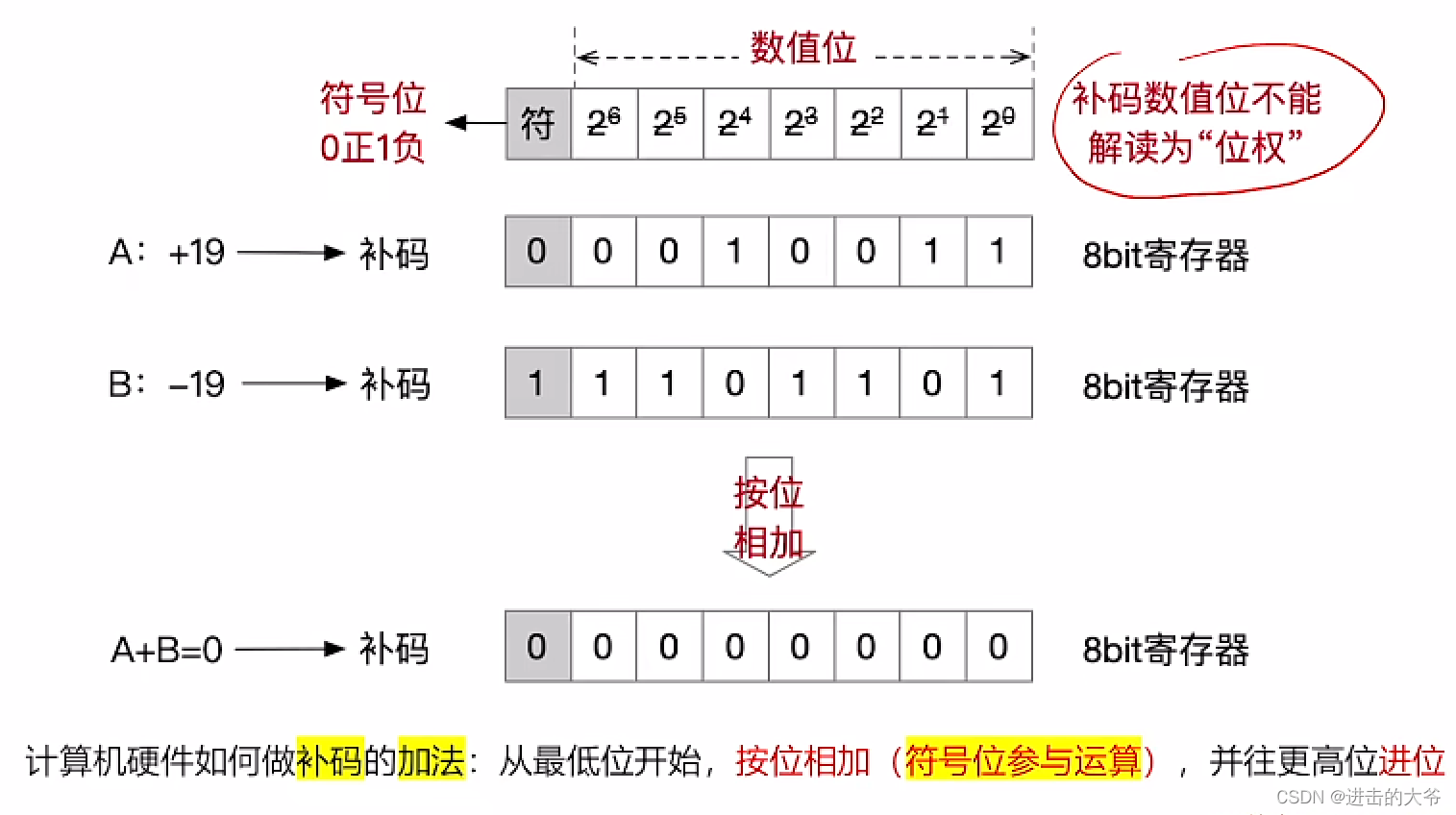
补码的加法运算(例2)
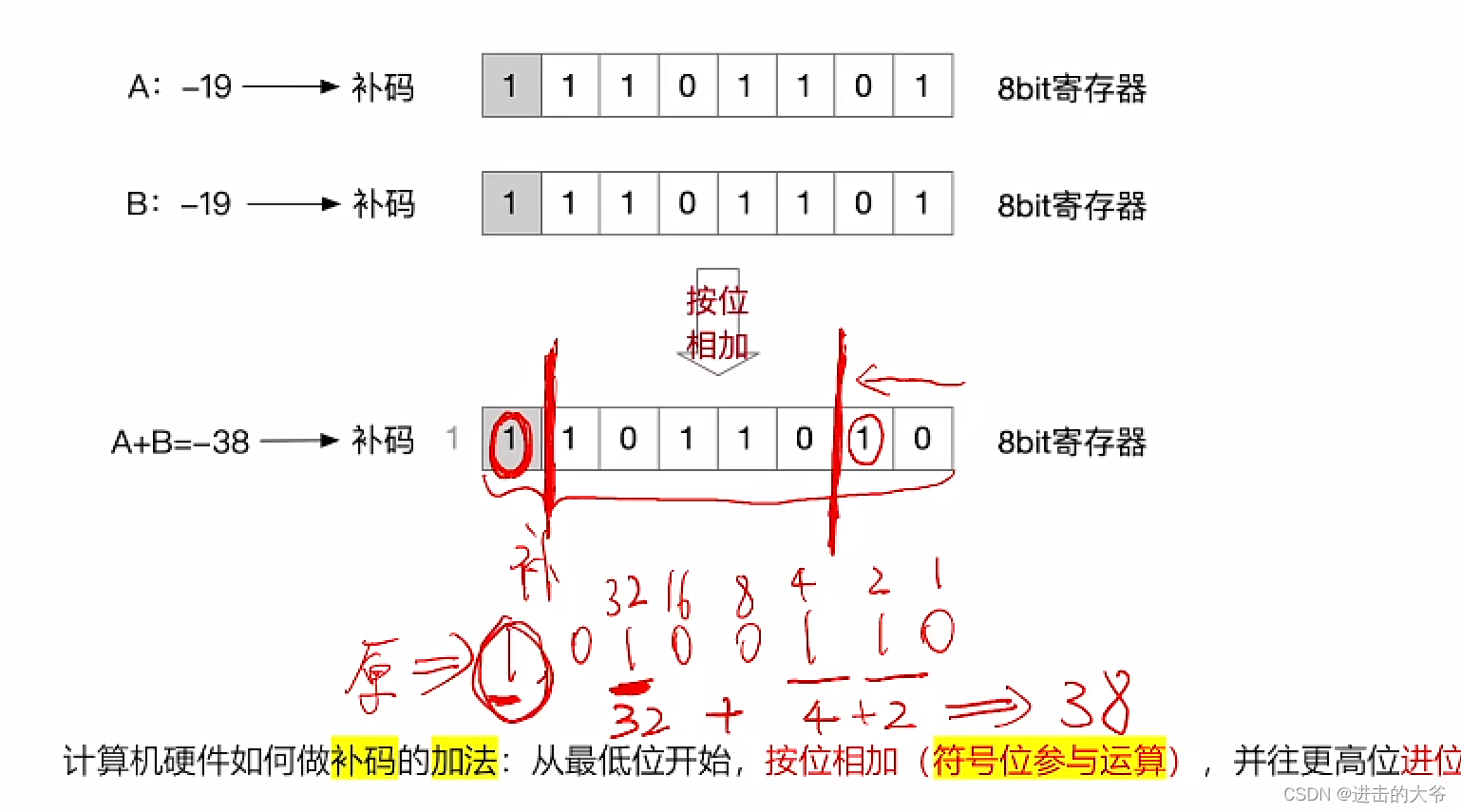
补码的减法运算
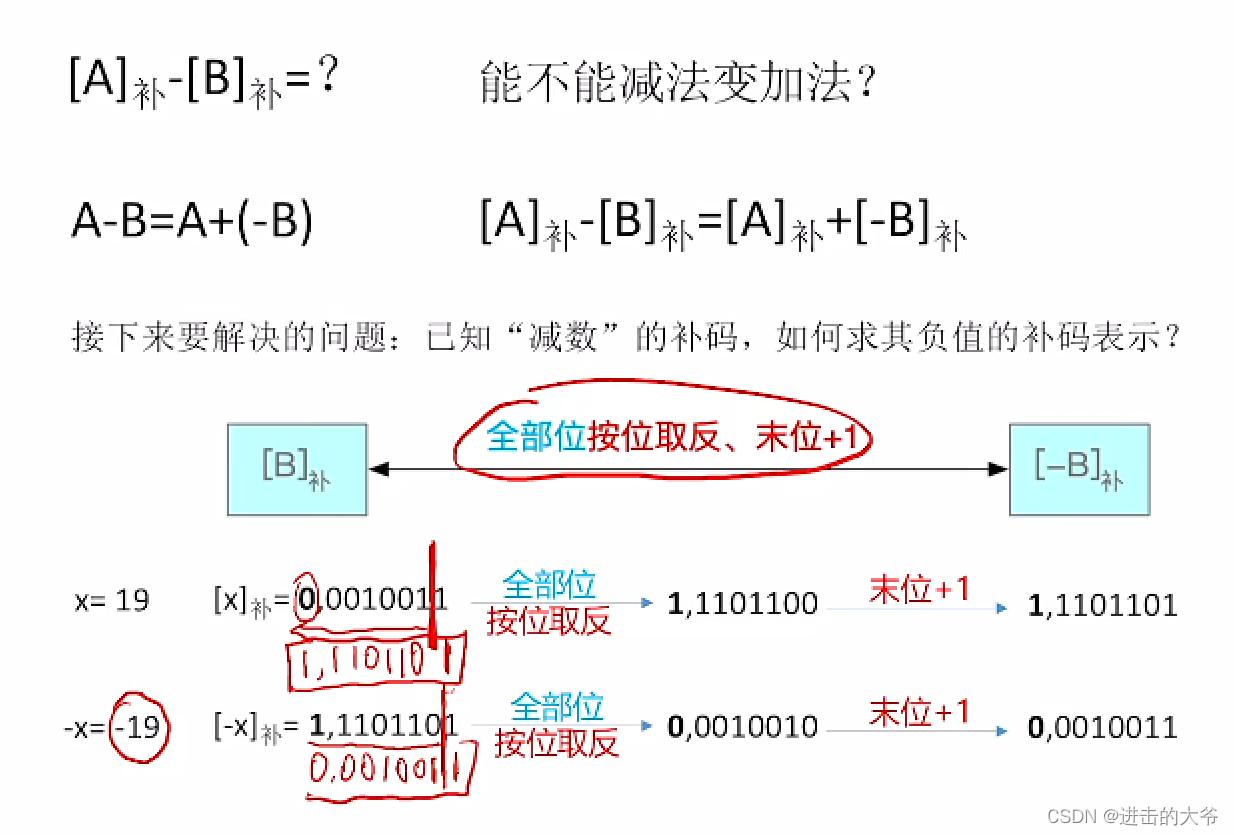
补码的减法运算(例3)
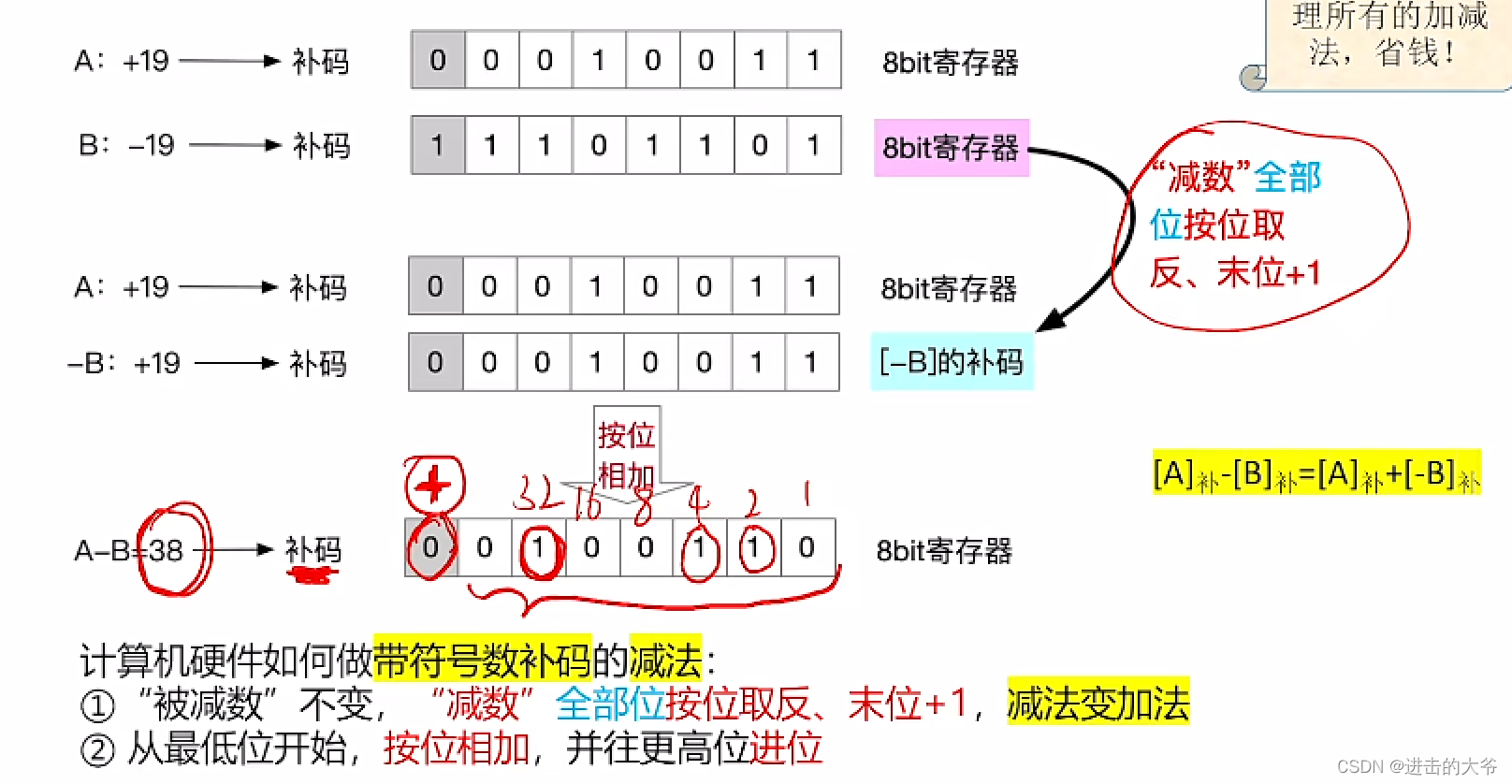
注:对比无符号整数的减法运算。优点:用同一套电路即可处理所有的加减法,省钱!
知识回顾与重要考点
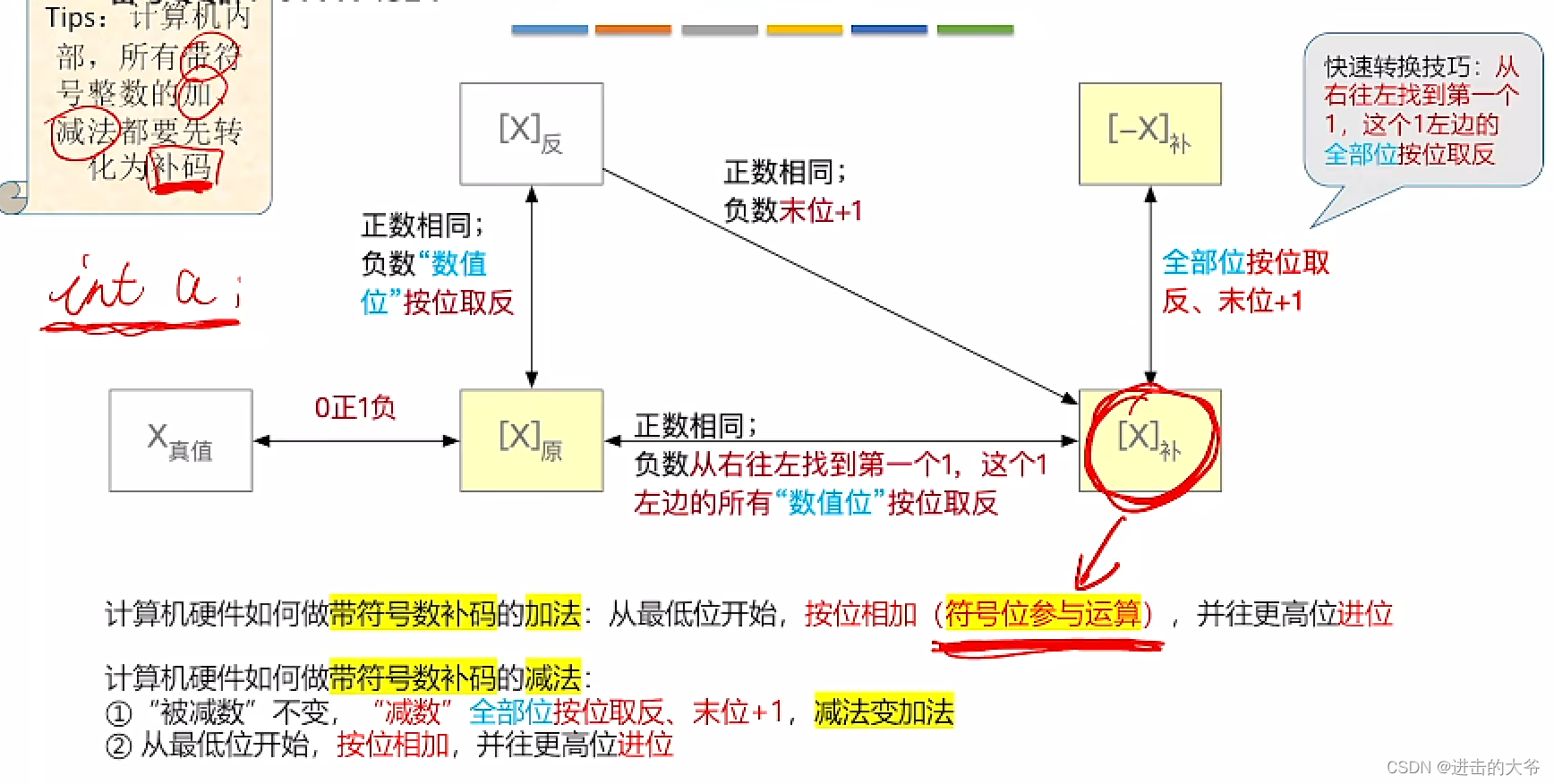
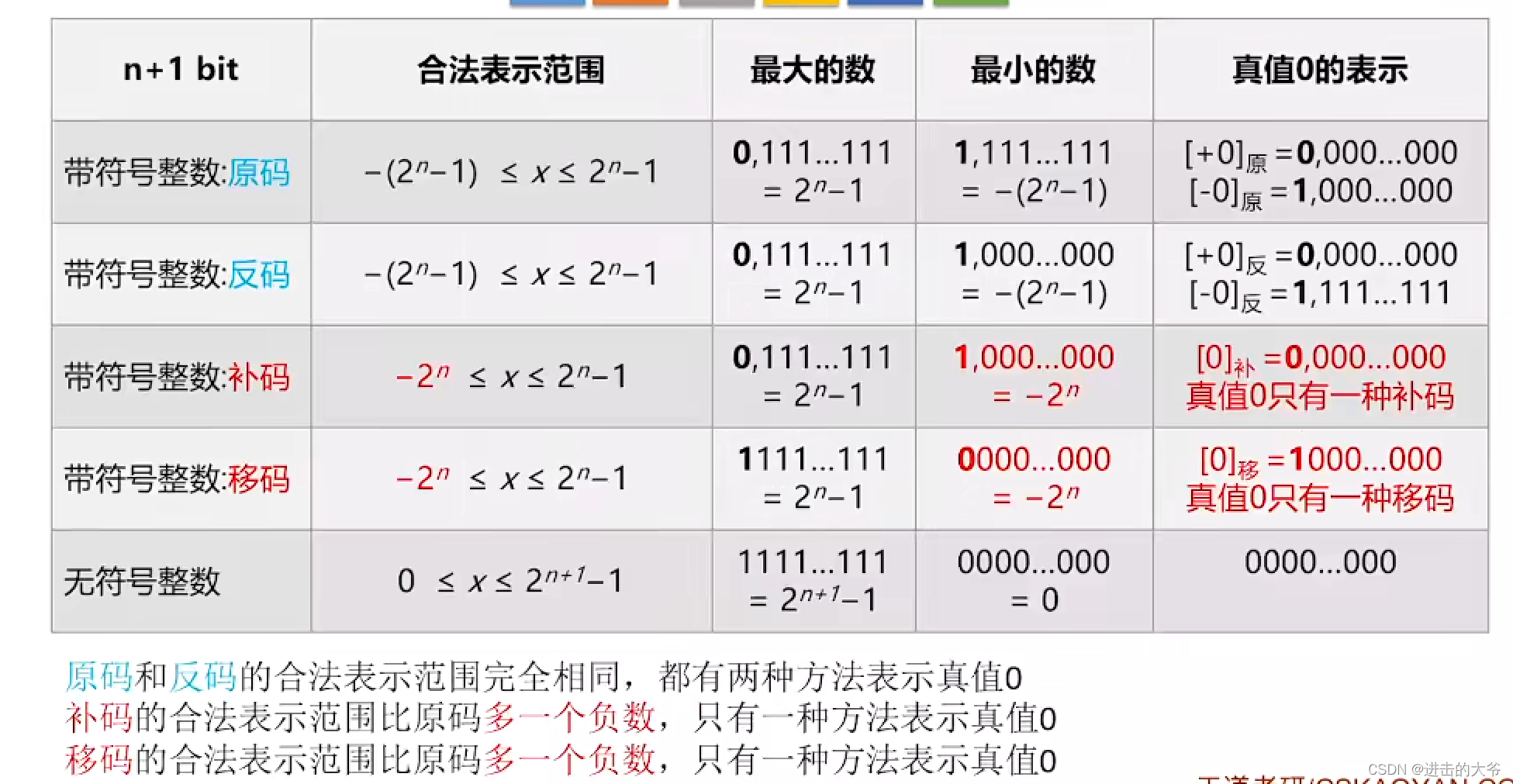
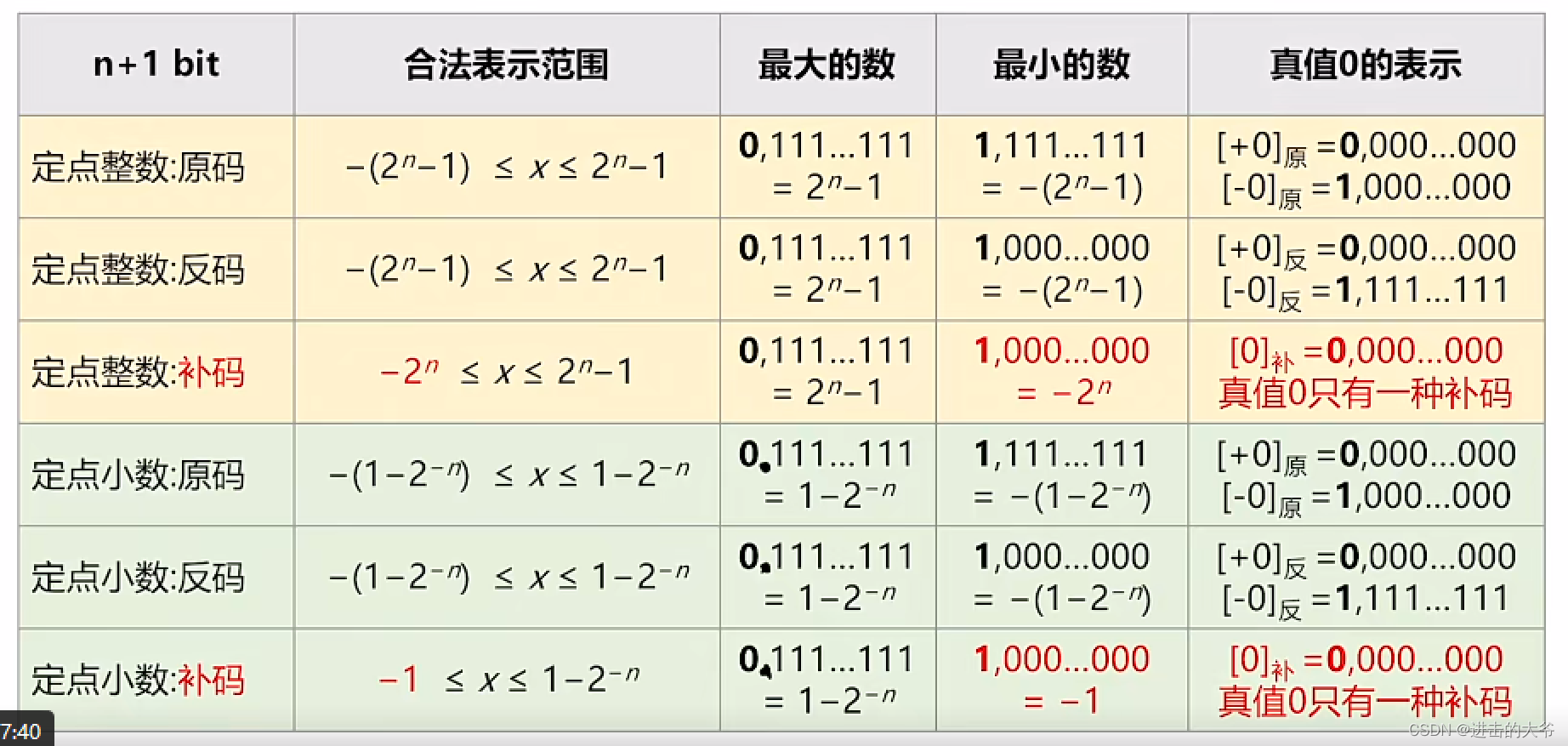
2.1.5 原反补码的特性对比
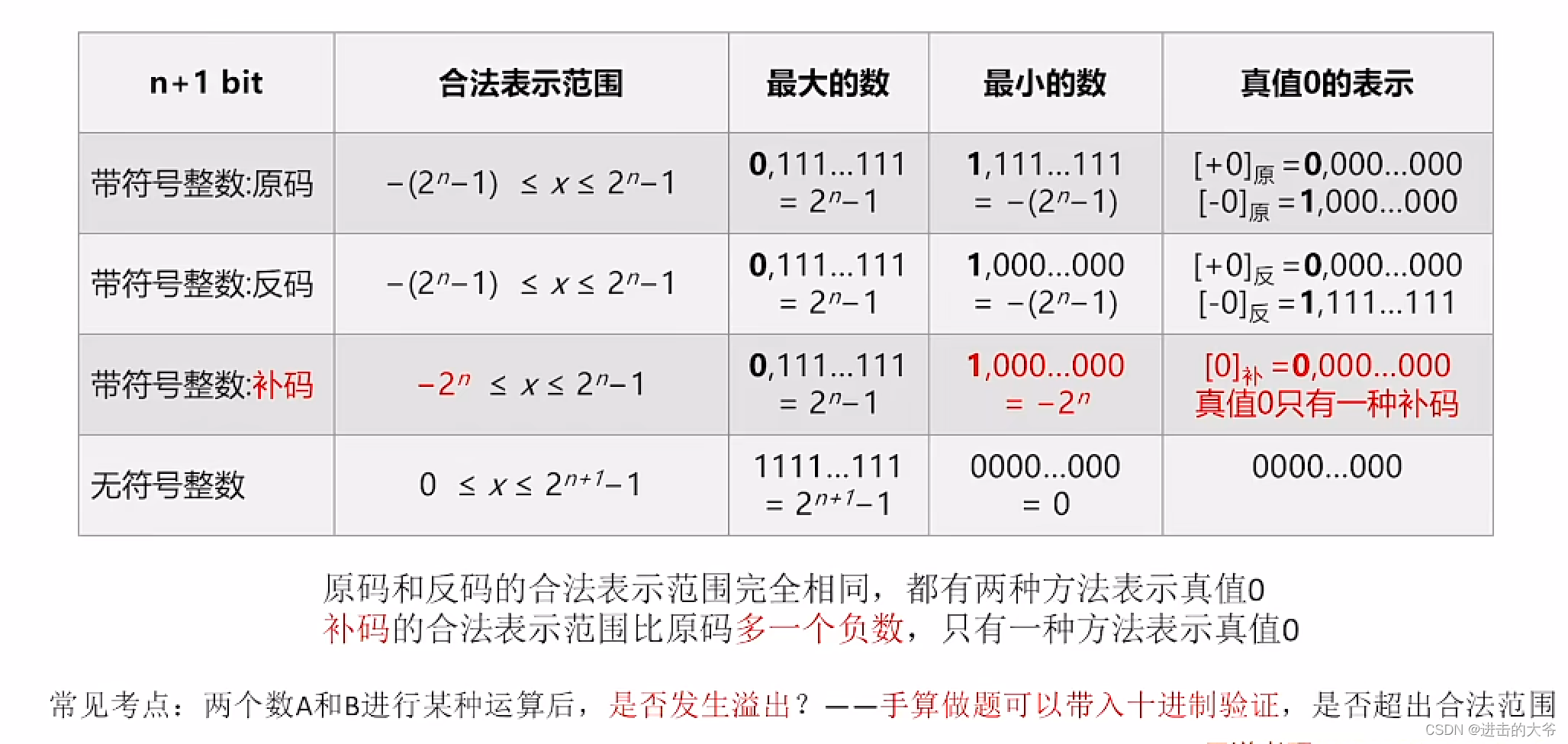
在这里插入图片描述
注:反码与原码表示的范围是一样的,当n是整数时,真值负数最小时,原码是1111 1111,反码是1000 0000。
2.1.6 移码
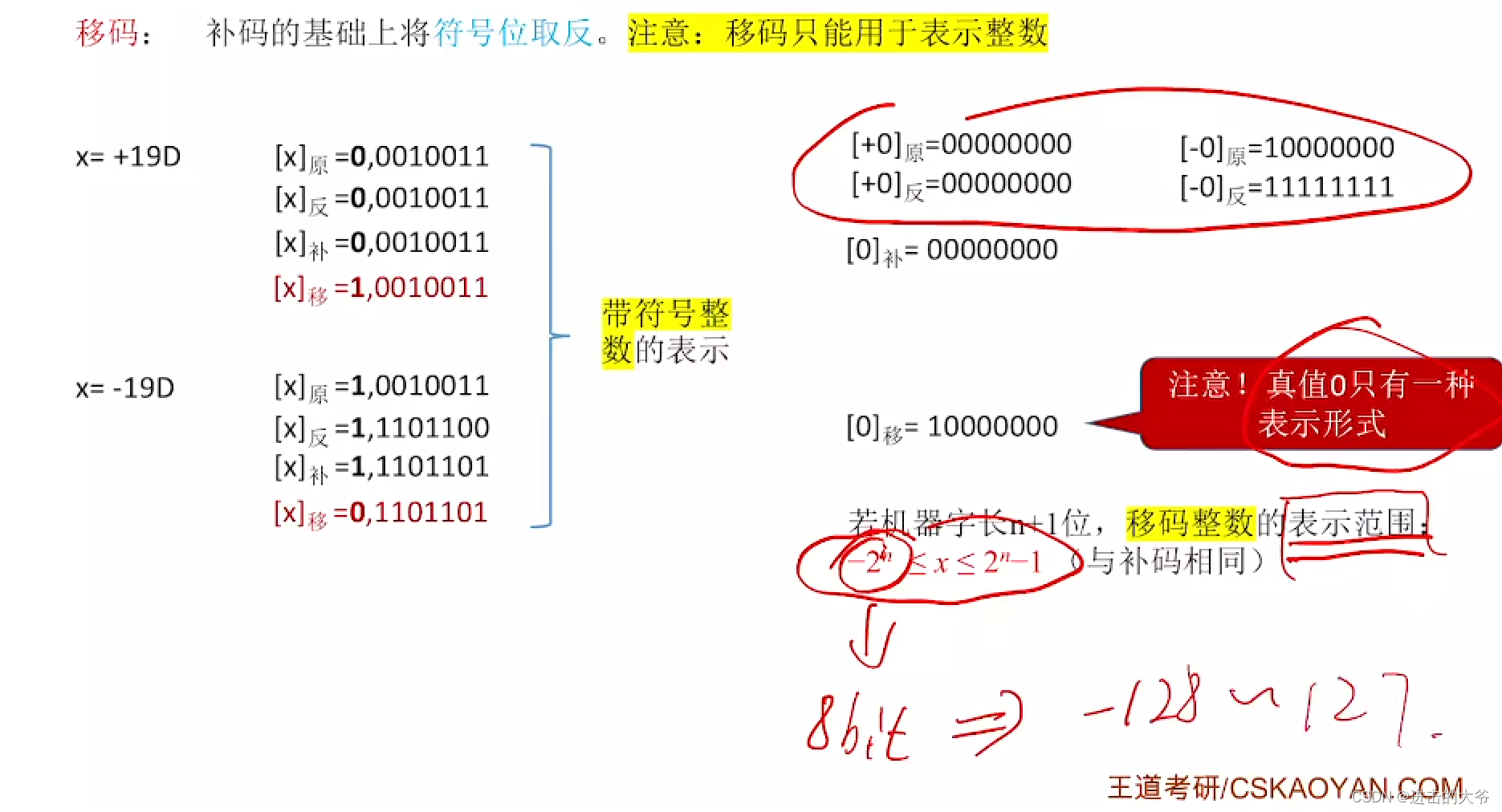
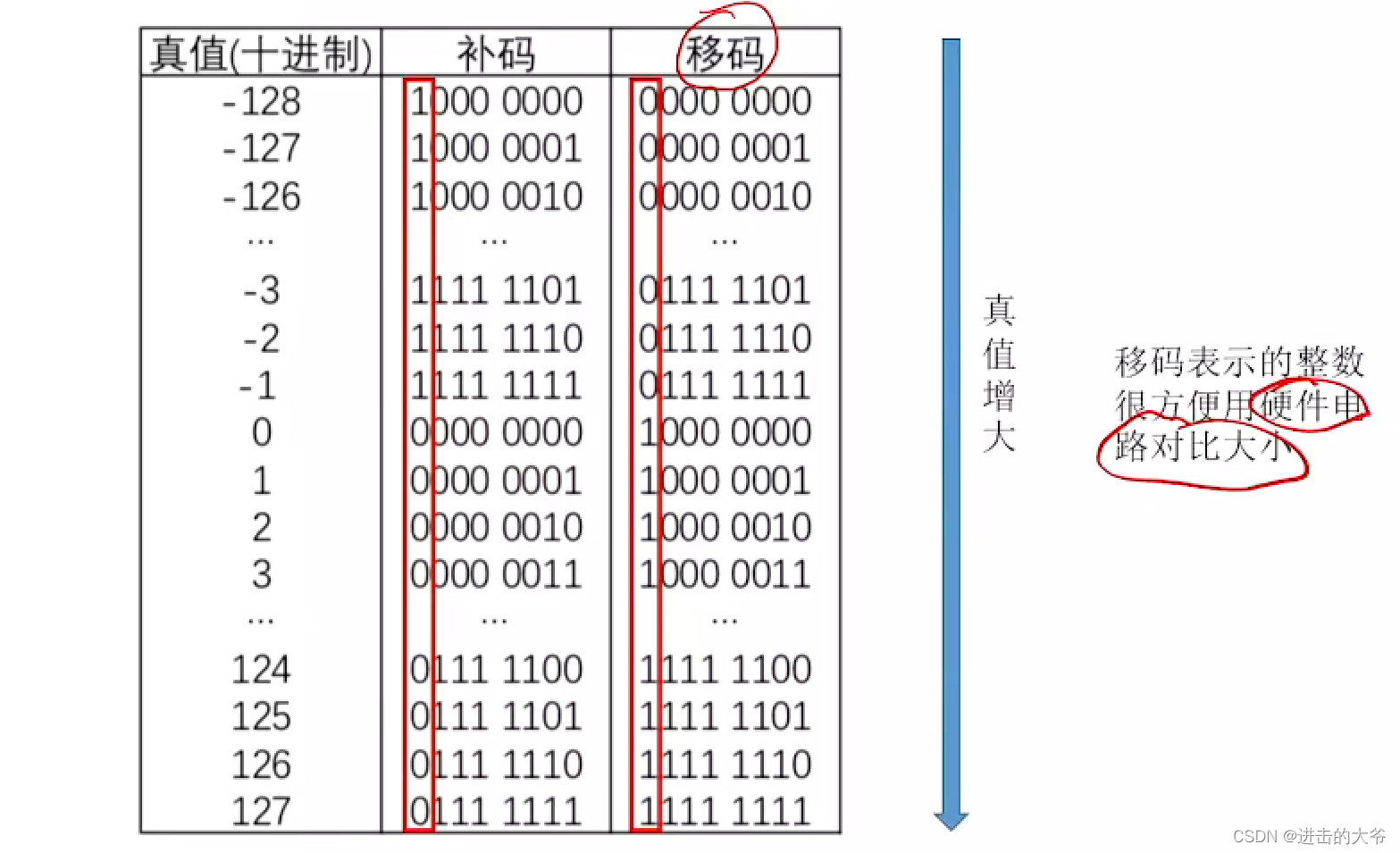
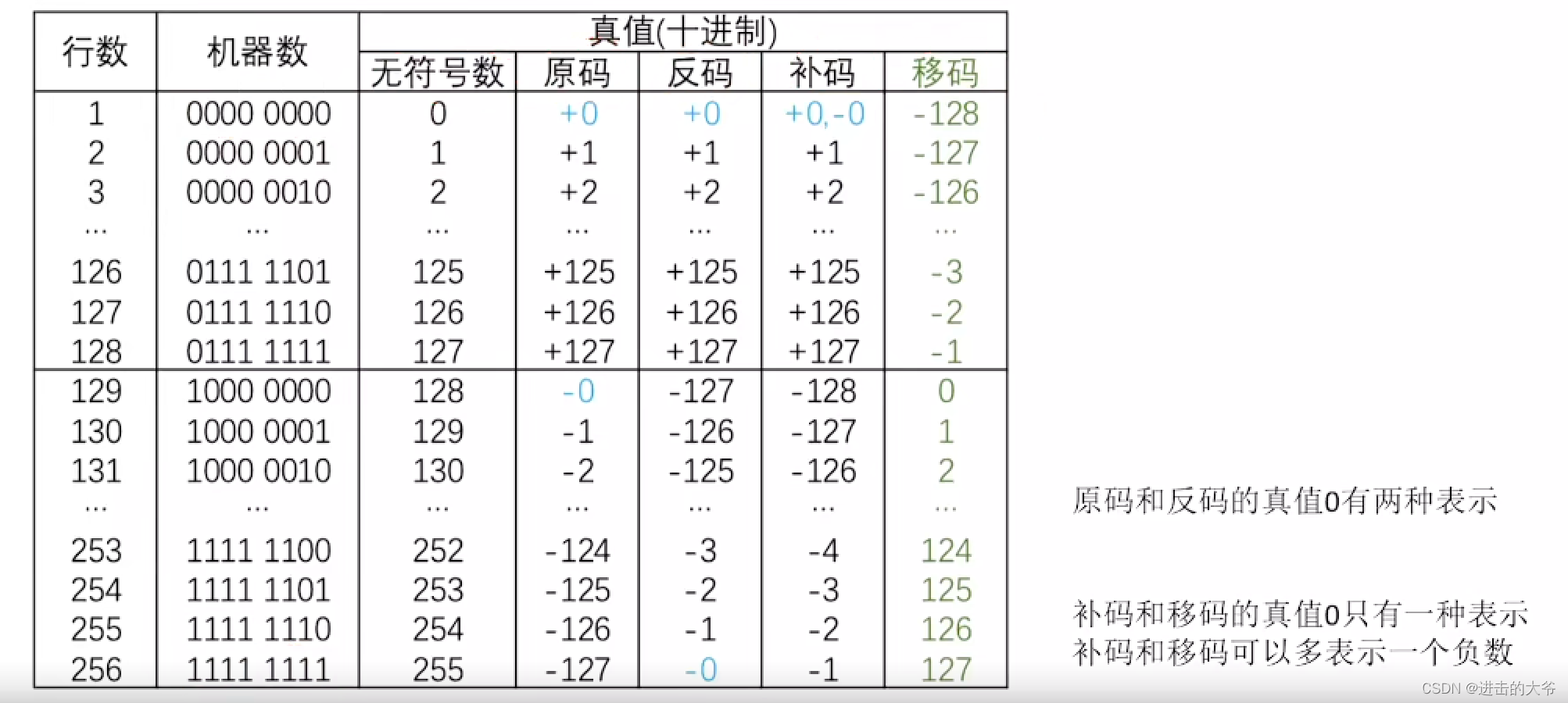
2.1.7 定点小数
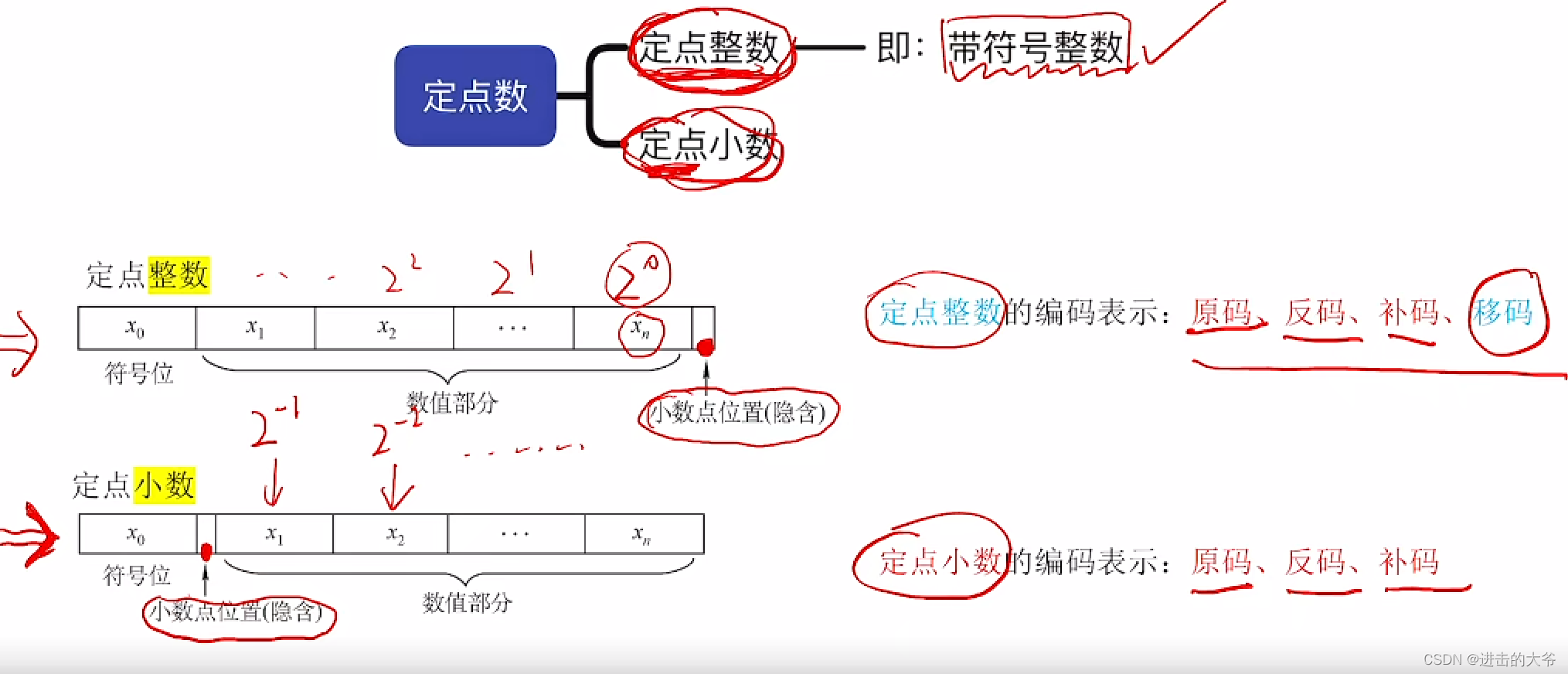
定点小数的原码
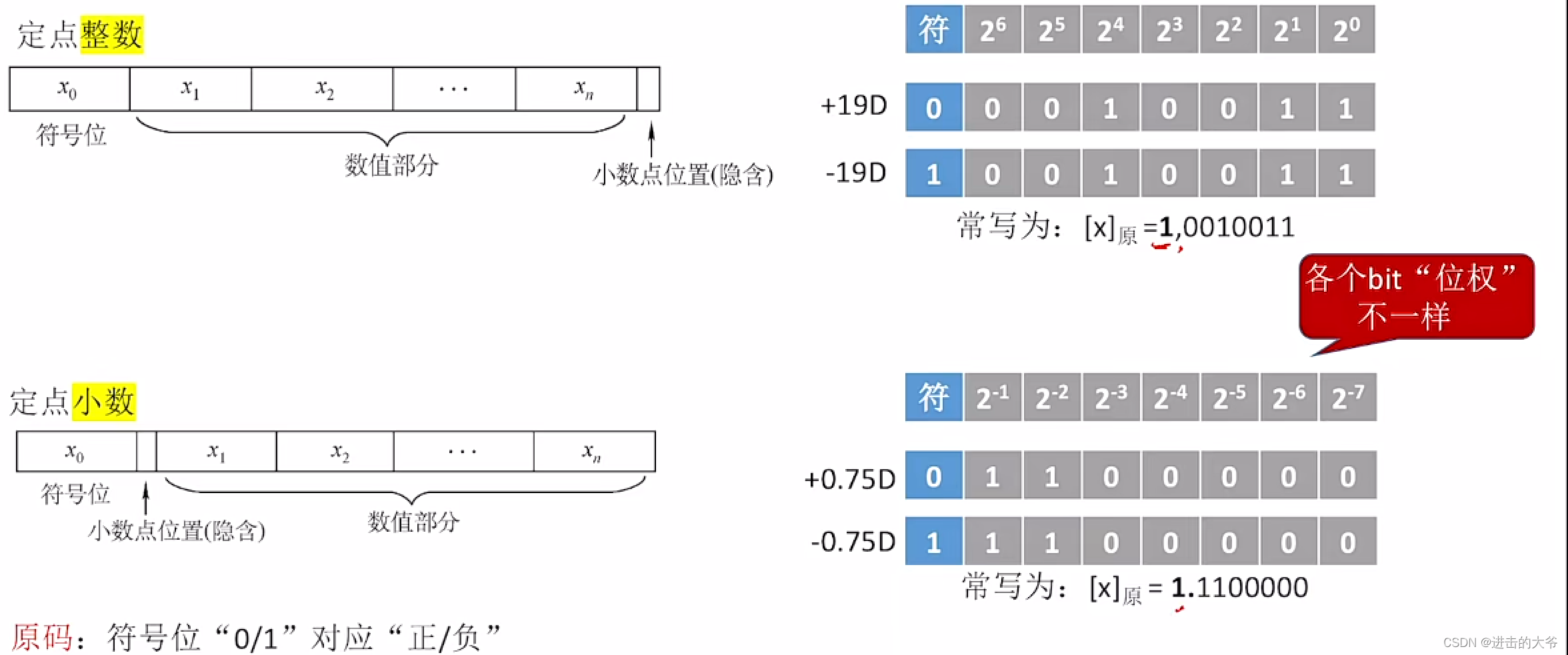
定点小数原反补码的转换
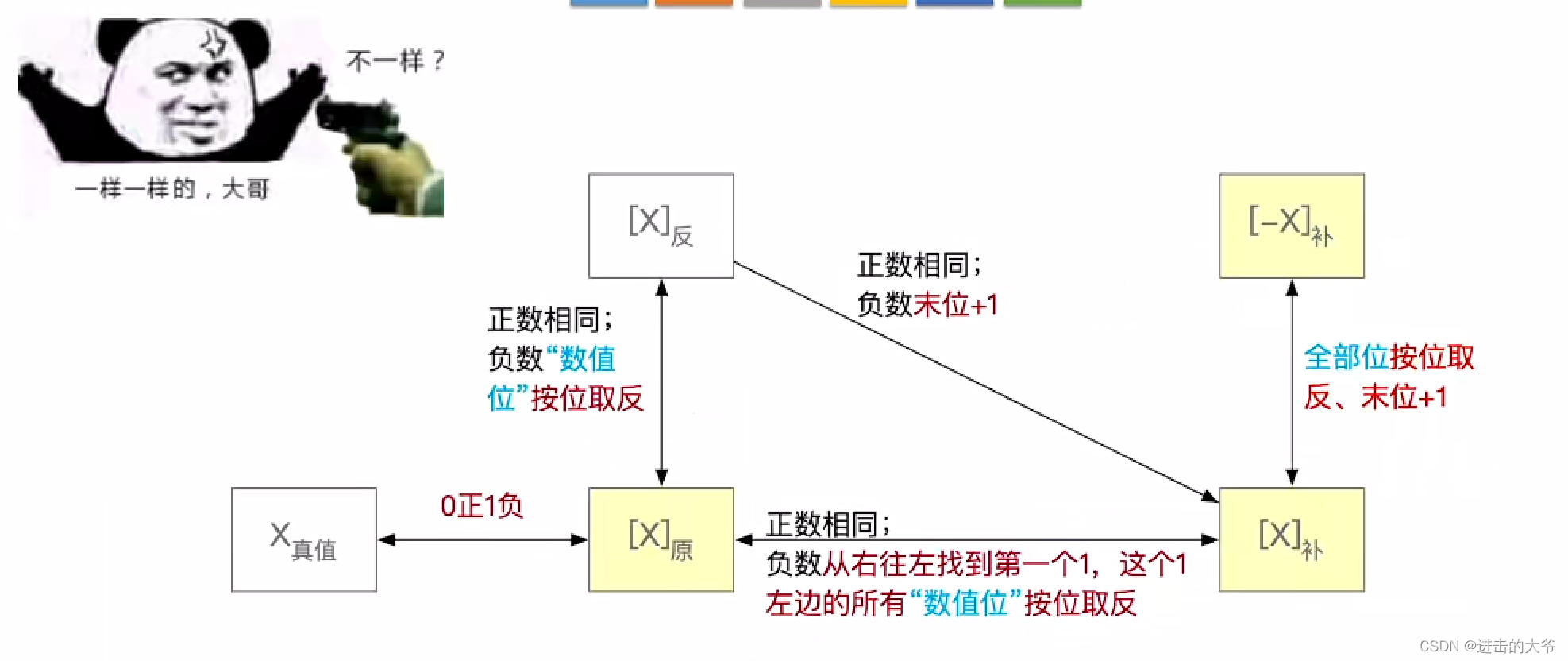
注:和定点整数一模一样。
定点小数的加减法运算

小数的加减运算和整数的处理逻辑是一样的。
定点小数VS定点整数

2.2


 浙公网安备 33010602011771号
浙公网安备 33010602011771号