[NOI 2016]区间

Description

在数轴上有 $n$ 个闭区间 $[l_1,r_1],[l_2,r_2],...,[l_n,r_n]$。现在要从中选出 $m$ 个区间，使得这 $m$ 个区间共同包含至少一个位置。换句话说，就是使得存在一个 $x$，使得对于每一个被选中的区间 $[l_i,r_i]$，都有 $l_i \le x \le r_i$。

对于一个合法的选取方案，它的花费为被选中的最长区间长度减去被选中的最短区间长度。区间 $[l_i,r_i]$ 的长度定义为 $r_i-l_i$，即等于它的右端点的值减去左端点的值。

求所有合法方案中最小的花费。如果不存在合法的方案，输出 $−1$。

Input

第一行包含两个正整数 $n,m$，用空格隔开，意义如上文所述。保证 $1 \le m \le n$。

接下来 $n$ 行，每行表示一个区间，包含用空格隔开的两个整数 $l_i$ 和 $r_i$ 为该区间的左右端点。

Output

只有一行，包含一个正整数，即最小花费。

Sample Input

6 3
3 5
1 2
3 4
2 2
1 5
1 4

Sample Output

2

Sample Explanation

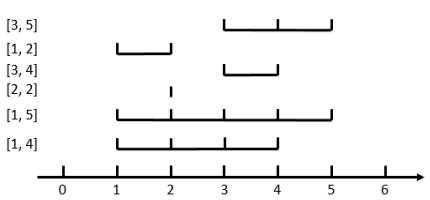
如图，当 $n=6,~m=3$ 时，花费最小的方案是选取 $[3,5]$、$[3,4]$、$[1,4]$ 这三个区间，他们共同包含了 $4$ 这个位置，所以是合法的。其中最长的区间是 $[1,4]$，最短的区间是 $[3,4]$，所以它的花费是 $(4−1)−(4−3)=2$。

Hint

所有测试数据的范围和特点如下表所示：

测试点编号	$n$	$m$	$l_i,r_i$
1	$20$	$9$	$0 \le l_i \le r_i \le 100$
2		$10$
3	$199$	$3$	$0 \le l_i \le r_i \le 100000$
4	$200$
5	$1000$	$2$
6	$2000$
7	$199$	$60$	$0 \le l_i \le r_i \le 5000$
8	$200$	$50$
9			$0 \le l_i \le r_i \le 10^9$
10	$1999$	$500$	$0 \le l_i \le r_i \le 5000$
11	$2000$	$400$
12		$500$	$0 \le l_i \le r_i \le 10^9$
13	$30000$	$2000$	$0 \le l_i \le r_i \le 100000$
14	$40000$	$1000$
15	$50000$	$15000$
16	$100000$	$20000$
17	$200000$		$0 \le l_i \le r_i \le 10^9$
18	$300000$	$50000$
19	$400000$	$90000$
20	$500000$	$200000$

时间限制：$3\texttt{s}$

空间限制：$256\texttt{MB}$

 

题解（转载）

->原文地址<-

首先发现那一个相交的点一定可以是区间的某个端点，所以可以离散左右端点，那么问题就简单了，然后仔细推敲，发现可以按区间长度排序，然后不就是尺取法了么?如果有一个点被覆盖的次数$>=m$我们就移动右指针，不然我们就一直往后走，对于覆盖次数$>=m$我们就维护线段树区间最大值，然后区间修改维护指针移动即可。

//It is made by Awson on 2017.10.17
#include <set>
#include <map>
#include <cmath>
#include <ctime>
#include <cmath>
#include <stack>
#include <queue>
#include <vector>
#include <string>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
#define LL long long
#define Min(a, b) ((a) < (b) ? (a) : (b))
#define Max(a, b) ((a) > (b) ? (a) : (b))
#define sqr(x) ((x)*(x))
#define Lr(x) (x<<1)
#define Rr(x) (x<<1|1)
using namespace std;
const int N = 500000;

int n, m, ans = 2e9;
struct tt {
  int l, r, val;
  bool operator < (const tt &b) const{
    return val < b.val;
  }
}a[N+5];
struct ss {
  int val, id, op;
  bool operator < (const ss &b) const{
    return val < b.val;
  }
}b[(N<<1)+5];
struct segment {
  int sgm[(N<<3)+5], lazy[(N<<3)+5];
  void pushdown(int o) {
    sgm[Lr(o)] += lazy[o], sgm[Rr(o)] += lazy[o];
    lazy[Lr(o)] += lazy[o], lazy[Rr(o)] += lazy[o];
    lazy[o] = 0;
  }
  void update(int o, int l, int r, int a, int b, int key) {
    if (a <= l && r <= b) {
      sgm[o] += key, lazy[o] += key;
      return;
    }
    pushdown(o);
    int mid = (l+r)>>1;
    if (a <= mid) update(Lr(o), l, mid, a, b, key);
    if (b > mid) update(Rr(o), mid+1, r, a, b, key);
    sgm[o] = Max(sgm[Lr(o)], sgm[Rr(o)]);
  }
}T;

void work() {
  scanf("%d%d", &n, &m);
  for (int i = 1; i <= n; i++) scanf("%d%d", &a[i].l, &a[i].r), a[i].val = a[i].r-a[i].l;
  sort(a+1, a+n+1);
  for (int i = 1; i <= n; i++) {
    b[(i<<1)-1].val = a[i].l, b[(i<<1)-1].id = i; b[i<<1].val = a[i].r, b[i<<1].id = i;
  }
  sort(b+1, b+2*n+1); b[0].val = -1;
  for (int i = 1; i <= (n<<1); i++) b[i].op = b[i-1].op+(b[i].val != b[i-1].val);
  for (int i = 1; i <= (n<<1); i++) { 
    if (b[i].val == a[b[i].id].l) a[b[i].id].l = b[i].op;
    if (b[i].val == a[b[i].id].r) a[b[i].id].r = b[i].op;
  }
  int tol = b[n<<1].op, r = 0;
  for (int i = 1; i <= n; i++) {
    while (r < n && T.sgm[1] < m) {
      r++; T.update(1, 1, tol, a[r].l, a[r].r, 1);
    }
    if (T.sgm[1] >= m) ans = Min(ans, a[r].val-a[i].val);
    else break;
    T.update(1, 1, tol, a[i].l, a[i].r, -1);
  }
  printf("%d\n", ans == 2e9 ? -1 : ans);
}
int main() {
  work();
  return 0;
}