DS博客作业05--树
DS博客作业05--树
1.本周学习总结
这周学习了有关树和二叉树的知识,其中大部分都是有关于二叉树的题目,在二叉树中了解到了先序遍历,中序遍历和后序遍历三种遍历树的方式,也同样有顺序储存结构和链表储存结构两种储存方式,因为链表储存方式比较方便,所以我在代码中基本上都是用的链表储存方式,感觉树与前面知识最大的不同点是用到了很多递归的知识,建树和遍历基本都需要递归来完成,因为前面对递归的学习不是很透彻,所以在树的作业方面还是有些难度,但树的递归还是可以通过自己画图来帮助理解,自己画出来每一步递归到了树的哪一个位置理解起来就会容易很多。这周还学习到了万能头文件 #include <bits/stdc++.h>,其中包含了c和c++中所有的头文件。
2.PTA实验作业
2.1.题目1: 表达式树
输入一行中缀表达式,转换一颗二叉表达式树,并求解
2.1.1设计思路
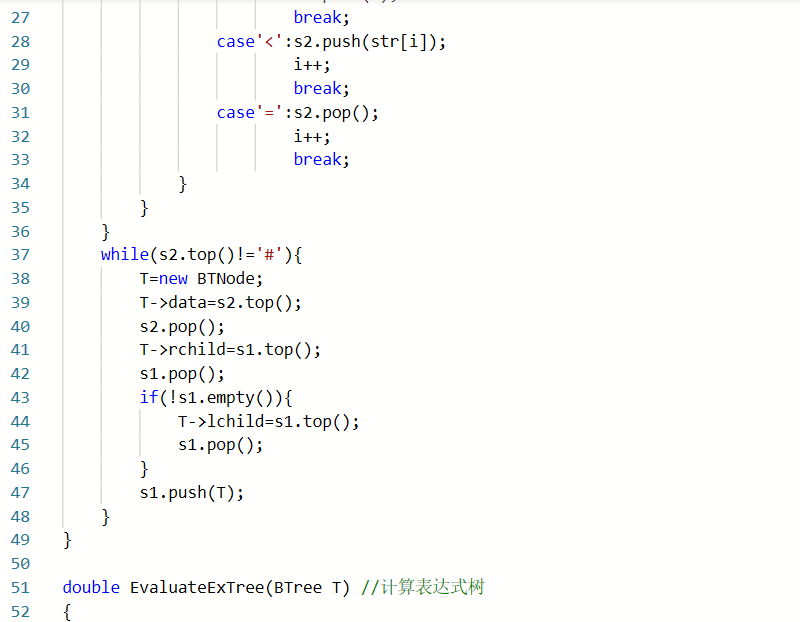
void InitExpTree(BTree &T,string str)
定义栈s1储存字符串中的数字
定义栈s2储存字符串中的运算符
将#入栈到s2
定义i并赋值为0
while str[i]≠0 do
if str[i]是数字
then 创建新结点T并赋值为str[i]
i++
T的左,右孩子都置为空
将T入栈到s1
else
switch(Precede(s2.top(),str[i]))
if '>'
then 创建新结点T并赋值为s2的栈顶元素值
s2进行出栈
T右孩子⬅s1栈顶元素
s1进行出栈
if s1不为空
then T左孩子⬅s1栈顶元素
s1进行出栈,并将T入栈s1
if '<'
then 将str[i]入栈到s2
i++
if '='
then s2出栈
i++
while(s2.top()≠'#')
创建新结点T并赋值为s2栈顶元素值
s2出栈
T右孩子⬅s1.top且s1进行出栈
T左孩子⬅s1.top且s1进行出栈
将T入栈到s1
double EvaluateExTree(BTree T) //计算表达式树
定义浮点型数a,b来运算时的两个数
if T为叶子结点
then T储存的字符转变为数字
a储存T左孩子 b储存T右孩子
switch(T->data)
if '+' then返回a+b
if '-' then返回a-b
if '*' then返回a*b
if '/' 且b≠0 then返回a/b
2.1.2代码截图


2.1.3本题PTA提交列表说明

Q1:在遇到除0时发生错误,程序异常终止
A1:在函数EvaluateExTree中判断除数是否为零时,只是单纯输出了除数为零时的提示语,运行的时候程序就是异常终止了,后来在输出提示语后加入一句exit(0)表示正常运行程序并退出,问题就解决了。
2.2 题目2:还原二叉树
给定一棵二叉树的先序遍历序列和中序遍历序列,要求计算该二叉树的高度。
2.2.1设计思路
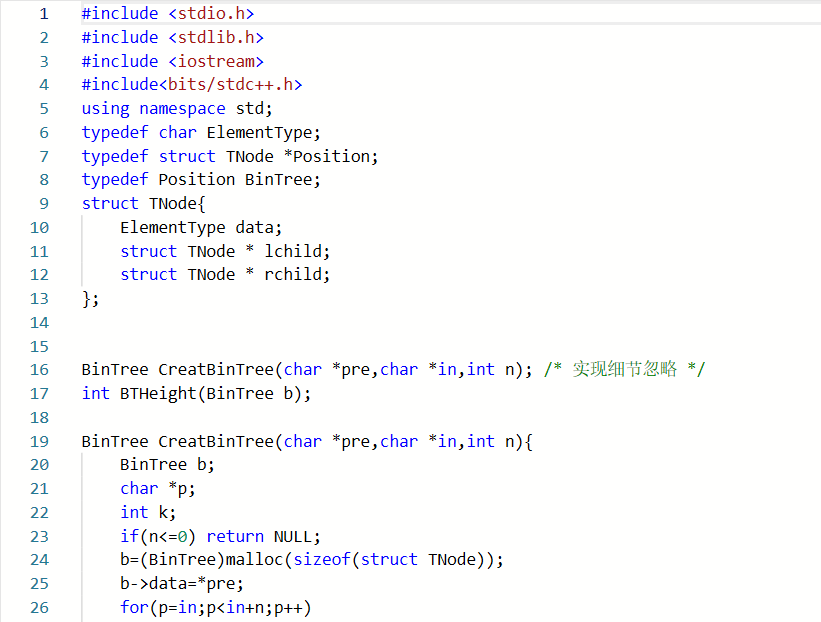
BinTree CreatBinTree(char *pre,char *in,int n)
pre存放先序序列,in存放中序序列,n为二叉树的结点个数
定义树形指针b,指针p,k
创建二叉树结点b
b->data⬅*pre
for p=in to p<in+n
then if pre指向根结点
在in中找到后退出循环
k保存根结点在in中的位置
递归构造左子树
递归构造右子树
return b
int BTHeight(BinTree b)
定义lchildh,rchildh分别储存左右子树的高度
if b=NULL
then 返回空树高度为0
else
利用递归求出左子树的高度lchildh
利用递归求出右子树的高度rchildh
2.2.2代码截图


2.2.3本题PTA提交列表说明

Q1:在构造二叉树时不知道怎么构造
A1:需要先定义两个数组来储存先序遍历和中序遍历时的序列,然后在中序序列中找等于*pre字符的位置并保存,最后确定根结点的位置就可以开始递归建树,在参考课本上的代码以后就基本可以写出这题的代码。
2.3 题目3:根据后序和中序遍历输出先序遍历
根据给定的一棵二叉树的后序遍历和中序遍历结果,输出该树的先序遍历结果。
2.3.1设计思路
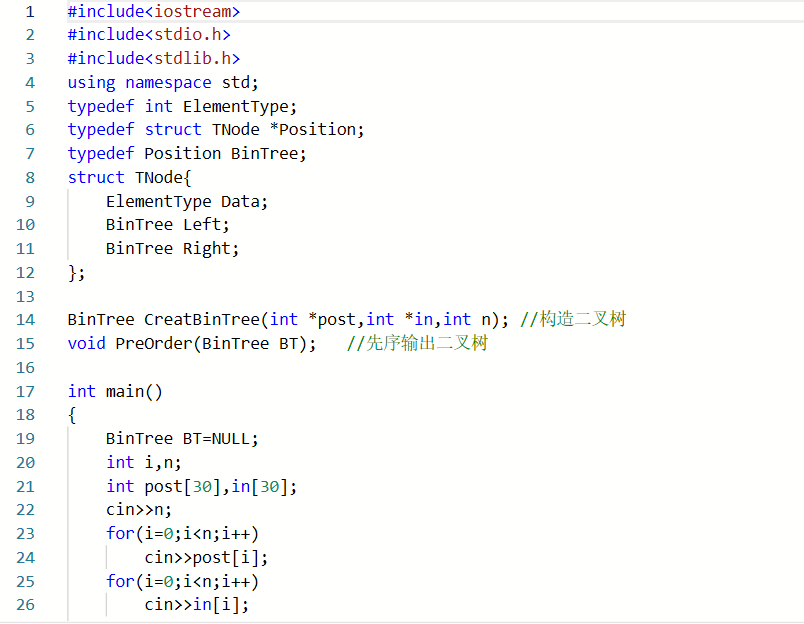
BinTree CreatBinTree(int *post,int *in,int n)
定义树形指针BT
定义指针r,*p
r储存根结点值*(post+n-1)
创建二叉树结点b
b->data⬅r
for p=in to p<in+n
在in中查找根结点值
end
k储存根结点在in中的下标
递归构造左子树
递归构造右子树
返回指针b
void PreOrder(BinTree BT)
if 树不为空
then
访问根结点
用递归先序遍历左子树
用递归先序遍历右子树
2.3.2代码截图
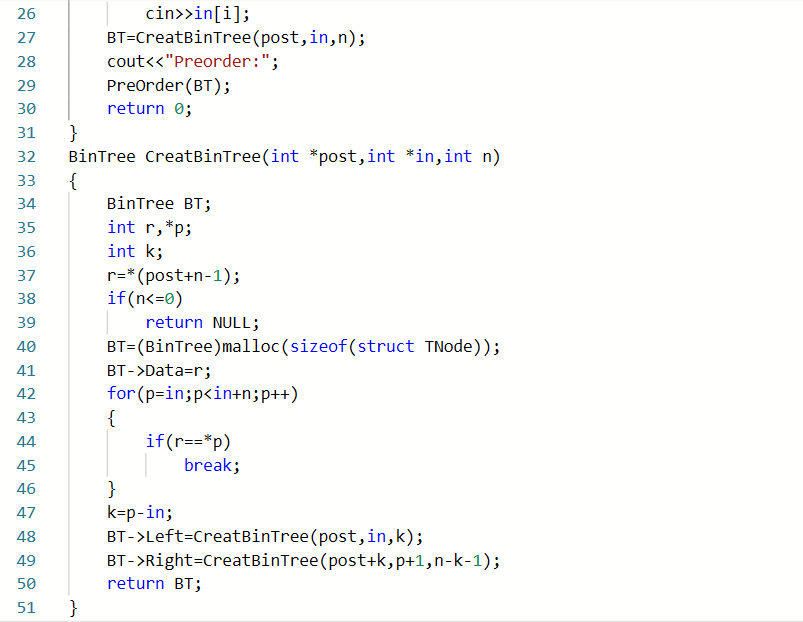

2.3.3本题PTA提交列表说明

Q1:无法输出结果
A1:这题虽然只有一次提交记录,但在编译器上还是出现了运行错误,无法输出任何结果,后来发现是在输入后序和中序序列时没有直接获取一串字符串,而是一个个字符的键入,就无法进行后面循环遍历,改为直接输入一串字符串后问题就解决了。
3、阅读代码
3.1 题目
求二叉树的最远两个结点的距离
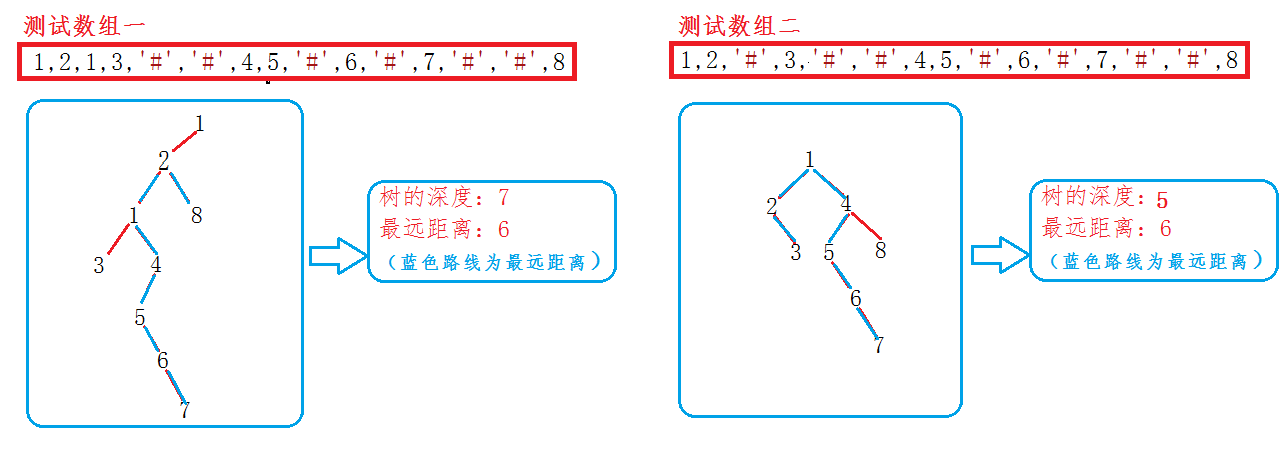
3.2 解题思路
该题先用先序递归建树,然后在求二叉树最远的两个结点的距离,利用递归不断往回带,求出二叉树的深度,最后比较到根结点,输出最远距离。
3.3 代码截图
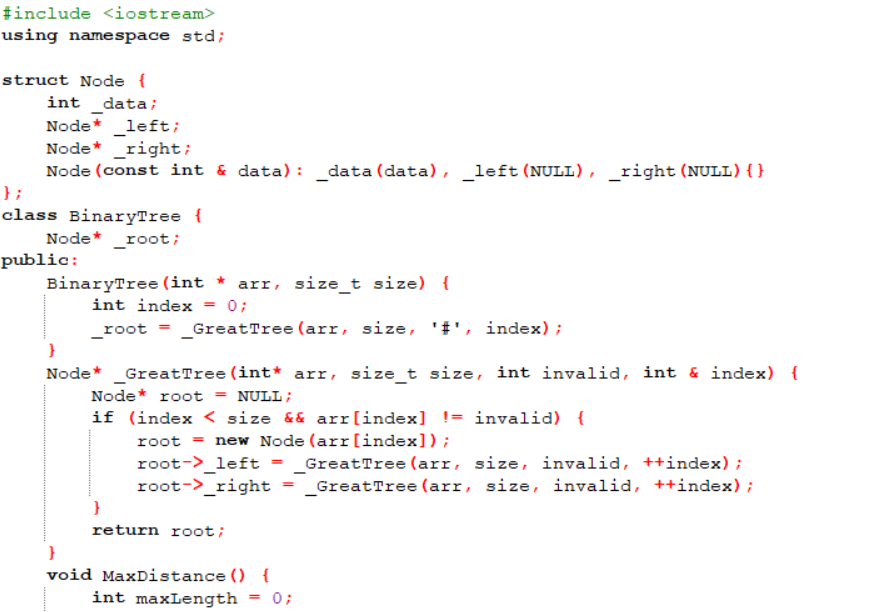
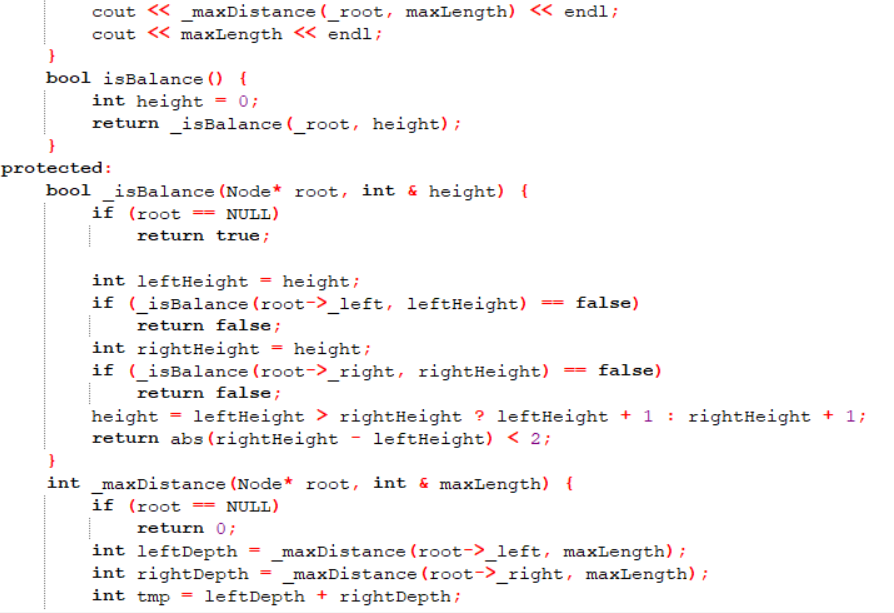

3.4 学习体会
这题利用递归求树的深度的思想,在其中加入一个最大距离的引用的参数,利用了引用参数的特性,求得最大距离,比较简单,但其中的代码涉及了三道有关于二叉树的题目:利用已知序列递归的建一棵二叉树;递归的求一棵树的深度;求二叉树中距离最远的两个节点的距离。利用这题类似的思想还可以判断一棵树是否为平衡二叉树。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号