2023-07-08 《数值优化方法》-庞丽萍,肖现涛-无约束最优化(四).md
2023-07-08 《数值优化方法》-庞丽萍,肖现涛-无约束最优化(四)
前面我们学习的二分法、成功-失败法、牛顿法、抛物线法都是精确求解一维问题 , 其中
, 其中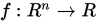 . 回到我们一开始的线搜索方法的目标是求解
. 回到我们一开始的线搜索方法的目标是求解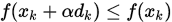 , 如果我们不求解当前的最优
, 如果我们不求解当前的最优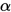 , 则称为非精确搜索法。
, 则称为非精确搜索法。
这里有个问题,牛顿法和抛物线法是近似求解了当前的最优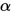 , 但是二分法和成功-失败法只是给出了每步的下降方向和给定的步长。#F44336
, 但是二分法和成功-失败法只是给出了每步的下降方向和给定的步长。#F44336
非精确线搜索准则有Armijo准则,Goldstein准则和Wolfe 准则,下面逐一介绍。
1. Armijo准则
设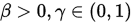 , 取步长
, 取步长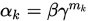 , 其中
, 其中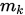 是满足下式的最小非负整数
是满足下式的最小非负整数
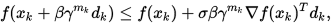
其中
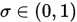 . 若上述不等式成立,则称步长
. 若上述不等式成立,则称步长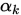 满足Armijo准则.
满足Armijo准则.
这里给以下Armijo准则的解释:(1)首先因为下降方向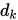 必然和梯度方向相反, 因此
必然和梯度方向相反, 因此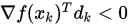 , 否则
, 否则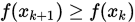 . (2) 此外
. (2) 此外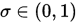 是因为当
是因为当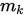 充分大时,上式即是一阶泰勒展开式,因此
充分大时,上式即是一阶泰勒展开式,因此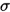 保证了不等式的成立.
保证了不等式的成立.
注意如果目标函数可导,则必然存在满足Armijo准则的步长.
2. Goldstein准则
若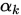 满足
满足
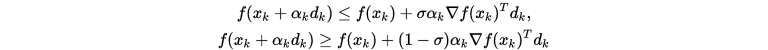
其中
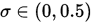 , 则称
, 则称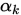 满足Goldstein准则.
满足Goldstein准则.
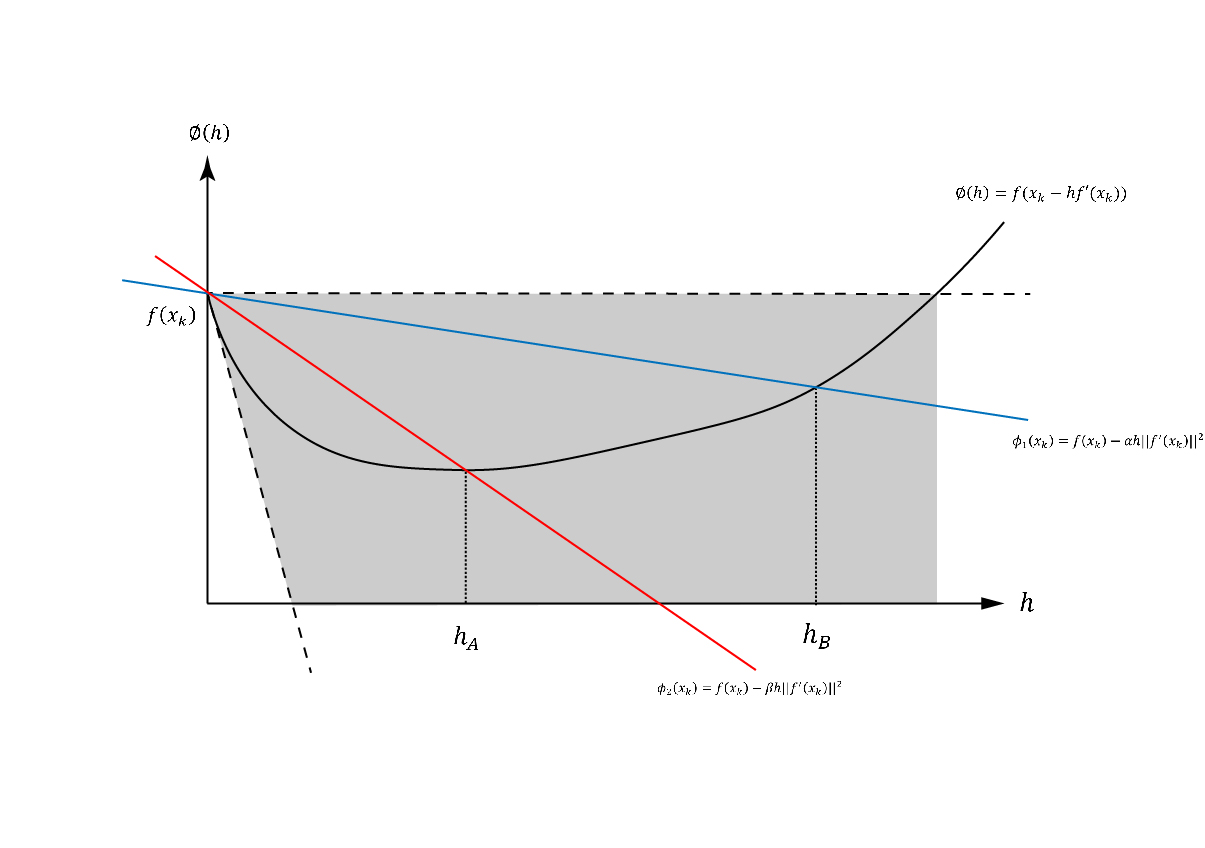
下面同样对Goldstein准则给出一些解释(应该会比书中清楚一些)
上图中由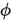 表示
表示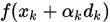 , 阴影部分表示
, 阴影部分表示 的可行区间(实际上
的可行区间(实际上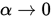 的部分也是可行的)
的部分也是可行的)
蓝色线表示第一个式子,即固定 下的新的
下的新的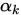 的可行域,红色线表示
的可行域,红色线表示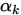 的最小值,最终
的最小值,最终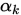 在三条线的交点之间。
在三条线的交点之间。
3. Wolfe准则(Armijo rule and curvature)
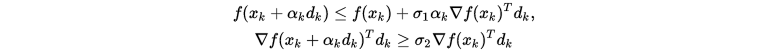
其中
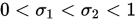 , 则称步长
, 则称步长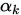 满足Wolfe准则。
满足Wolfe准则。
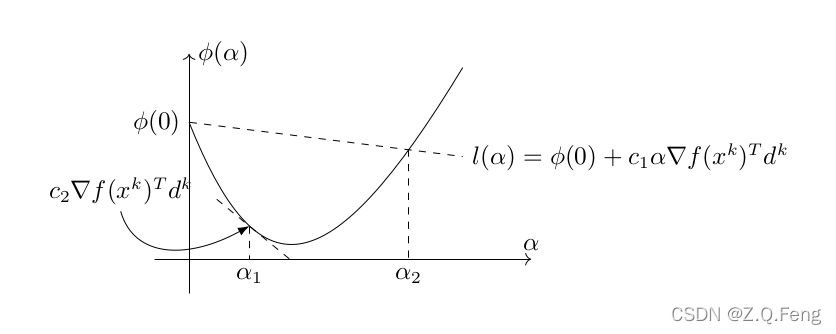
第一个式子即Armijo准则,我们来看第二个式子,注意到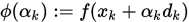 , 则
, 则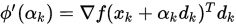 , 式子的右边即是
, 式子的右边即是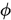 在
在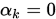 处导数的
处导数的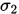 倍. 现在第二个式子的含义就很明显了,首先
倍. 现在第二个式子的含义就很明显了,首先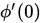 显然必然小于0, 然后第二个式子保证了
显然必然小于0, 然后第二个式子保证了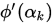 也是小于0, 则
也是小于0, 则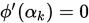 的点必然在第二个式子要求的右侧,结合第一个式子,可知Wolfe准则必然包含最优的
的点必然在第二个式子要求的右侧,结合第一个式子,可知Wolfe准则必然包含最优的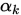 .
.
其中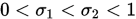 并没有查到这样设置的原因,但是在Wiki中看到了它的经验设置:
并没有查到这样设置的原因,但是在Wiki中看到了它的经验设置: is usually chosen to be quite small while
is usually chosen to be quite small while 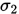 is much larger; Nocedal and Wright give example values of
is much larger; Nocedal and Wright give example values of 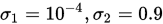 for Newton or quasi-Newton methods, and
for Newton or quasi-Newton methods, and 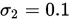 for nonlinear conjugate gradient method.#F44336
for nonlinear conjugate gradient method.#F44336
4. 强Wolfe准则(Strong Wolfe condition on curvature)
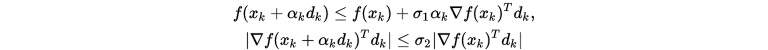
强Wolfe准则将
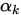 的可行区间削减到了更小的范围 (与
的可行区间削减到了更小的范围 (与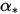 更接近).
更接近).
四种非精确线搜索准则的总结
Armijo准则给处的搜索步长保证了迭代是单调下降的,但是由于没有限制最小步长,因此可能导致迭代不收敛到极小值.
为了解决Armijo步长过小的问题,Goldstein根据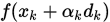 在
在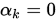 处的斜率生成了两条直线,将步长限制在两条直线与曲线
处的斜率生成了两条直线,将步长限制在两条直线与曲线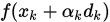 的交点范围内.
的交点范围内.
由于Goldstein准则可能将最优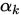 的取值舍弃,因此Wolfe提出了曲率准则,始终保证了最优
的取值舍弃,因此Wolfe提出了曲率准则,始终保证了最优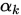 在取值范围内.
在取值范围内.
为了将取值范围进一步缩小,再改进了Wolfe准则,即得到强Wolfe准则.#3F51B5
5. 非精确线搜索的算法框架
前述非精确线搜索在优化算法中都扮演的确定最优步长的角色,而下降方向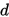 都假设已知。下面给出非精确线搜索Goldstein的算法框架:
都假设已知。下面给出非精确线搜索Goldstein的算法框架:
Step 1. 在搜索区间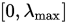 中选择初始点
中选择初始点 , 给出可接受系数
, 给出可接受系数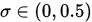 , 增大试探点系数
, 增大试探点系数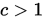 , 令
, 令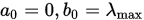 ,
, 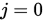 .
.
Step 2. 计算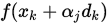 , 若
, 若
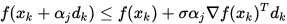
成立,转Step 3; 否则令
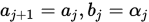 , 转Step 4.
, 转Step 4.
Step 3. 若
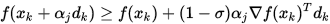
成立,则停止,置
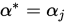 , 否则令
, 否则令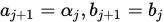 , 转 Step 4.
, 转 Step 4.
Step 4. 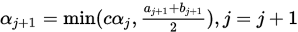 , 转Step 2.
, 转Step 2.
此算法和书中算法在Step 3 和 Step 4有些许不同,这里的算法感觉更清楚一些.
最后附上代码:
一维问题的非精确搜索算法
- function [alpha] = NonAccSearch(f, x0, method)
- % 转为符号函数
- if isa(f,'function_handle')
- syms x;
- fun(x) = f(x);
- fun_h = f;
- else
- fun = f;
- fun_h = matlabFunction(fun);
- end
- diff_fun1 = diff(fun);
- diff_h = matlabFunction(diff_fun1);
- if method == "Armijo"
- beta = 2;
- gamma = 0.5;
- sigma = 0.5;
- for i = 1:1e4
- d = - diff_h(x0);
- alpha = beta * gamma^i;
- LF = fun_h(x0 + alpha * d);
- RF = fun_h(x0) - sigma * alpha * d' * d;
- if LF <= RF
- break;
- end
- end
- end
-
- if method == "Goldstein"
- a = 0;
- b = 100;
- sigma = 0.01;
- c = 2;
- alpha = (a+b)/2;
- for k = 1:1e4
- d = - diff_h(x0);
- alpha = min((a+b)/2, c * alpha)
- LF = fun_h(x0 + alpha * d);
- RF = fun_h(x0) - sigma * alpha * d' * d;
- if LF <= RF
- F = fun_h(x0) - (1-sigma) * alpha * d' * d;
- if LF >= F
- break;
- end
- a = alpha;
- else
- b = alpha;
- end
- end
- end
- end
特别的,这里给出一个多维情况下的Armijo搜索,基于符号运算
- function [alpha] = NonAccSearchVec(f, A, x0, method)
- fun = f;
- fun_h = f;
- for i = 1:length(A)
- diff_fun1(i,1) = diff(fun, A(i));
- end
- diff_h = matlabFunction(diff_fun1);
- x0 = num2cell(x0);
- if method == "Armijo"
- beta = 2;
- gamma = 0.5;
- sigma = 0.5;
- for i = 1:1e4
- d = - diff_h(x0{:});
- alpha = beta * gamma^i;
- x1 = cell2mat(x0)' + alpha * d;
- x1 = num2cell(x1);
- LF = fun_h(x1{:});
- RF = fun_h(x0{:}) - sigma * alpha * d' * d;
- if LF <= RF
- break;
- end
- end
- end
- end
测试代码
- n = 10;
- A = sym('a', [n 1]);
- f(A) = sum(A.^2 - A);
- B = num2cell(1:n);
- f(B{:})
- x0 = repelem(0,n)
- [alpha] = NonAccSearchVec(f, A, x0, 'Armijo')
这里特别注意符号运算和参数输入等情况,个人感觉是很有价值的.

 浙公网安备 33010602011771号
浙公网安备 33010602011771号