2023-07-06 《数值优化方法》-庞丽萍,肖现涛-无约束最优化(二).md
2023-07-06 《数值优化方法》-庞丽萍,肖现涛-无约束最优化(二)
在(一)中我们提到过下降算法即是按照迭代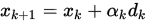 , 其中
, 其中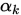 为步长,
为步长,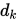 为下降方向。在射线
为下降方向。在射线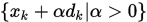 上寻求合适的步长,即所谓的一维线搜索,问题可表述为:
上寻求合适的步长,即所谓的一维线搜索,问题可表述为:
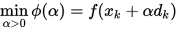
称在此最优意义下的步长
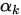 为最优步长或精确线搜索步长,称这种确定步长的方法为精确线搜索。上述问题的最优性条件为
为最优步长或精确线搜索步长,称这种确定步长的方法为精确线搜索。上述问题的最优性条件为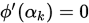 , 即是(正交性条件)
, 即是(正交性条件)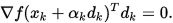
由于最优步长的的精确解不一定能得出或难以计算,因此考虑求解最优步长的数值解法,主要有
试探法
二分法
成功-失败法
函数逼近法(用简单函数的极小点来近似原函数的极小点)
牛顿法
抛物线法
1. 二分法
二分法是很经典的逼近方法,其要求目标函数是一维且可导的,且在试探区间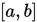 上
上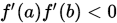 . 算法的思路简单,如下所示:
. 算法的思路简单,如下所示:
算法 1 二分法
Step 1. 设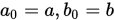 ,
, 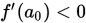 ,
, 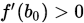 , 给定终止条件
, 给定终止条件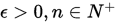 ,
, 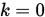 .
.
Step 2. 令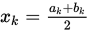 , 若
, 若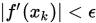 , 令
, 令 并停止, 否则转下步.
并停止, 否则转下步.
Step 3. 若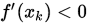 , 置
, 置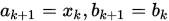 , 否则
, 否则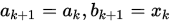 . 转下步.
. 转下步.
Step 4. 若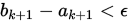 , 则记
, 则记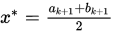 并停止,否则转下步.
并停止,否则转下步.
Step 5. 若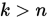 , 令
, 令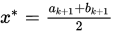 并停止,否则
并停止,否则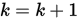 并转Step 2.
并转Step 2.
上述二分法是书中给出的,但是有的地方没有给出必要的说明。首先算法中对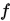 没有凸性要求,那么
没有凸性要求,那么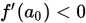 ,
, 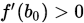 情况下二分法可能收敛到局部最优解上. 此外,如果
情况下二分法可能收敛到局部最优解上. 此外,如果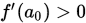 ,
, 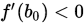 ,若
,若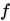 同时是凸函数,则最小值肯定在两个端点处,而若
同时是凸函数,则最小值肯定在两个端点处,而若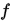 不是凸函数,那么上述二分法找到的是极大点.
不是凸函数,那么上述二分法找到的是极大点.
附上对应的Matlab代码,经过改进(自动找到满足条件的ab)
- % 一维最优化问题的二分搜索
- % fun 函数名称, 或匿名函数
- % a,b区间,其中a<b
- % epsil 指定终止条件(精度)
- % maxIt 最大迭代次数
- % bifact 表示加权系数,默认0.5
- function [xk xlog] = BisectionInt(fun, a, b, epsil, maxIt, bifact)
- if nargin < 6
- bifact = 0.5
- end
- alpha = bifact;
- beta = 1 - alpha;
- diff_fun = diff(fun);
- diff_fa = double(diff_fun(a));
- diff_fb = double(diff_fun(b));
- % 如果端点满足导数为0的条件
- if abs(diff_fa) < epsil
- xk = a;
- xlog = a;
- elseif abs(diff_fb) < epsil
- xk = b;
- xlog = b;
- elseif diff_fa < 0 && diff_fb > 0
- % 找到一个导数为0的点,此点是局部最优解
- [xk xlog] = Bisection(a, b, epsil, maxIt, diff_fun, alpha, beta);
- else
- % 非标准二分法
- % 先尝试能否找到满足标准二分法的端点
- h = (b-1)/1000;
- ha = a;
- hb = b;
- while double(diff_fun(ha)) > 0 && ha < b
- ha = ha + h;
- end
- while double(diff_fun(hb)) < 0 && hb > a
- hb = hb - h;
- end
- if hb > ha
- %找到了这样的端点
- [xk xlog] = Bisection(ha, hb, epsil, maxIt, diff_fun, alpha, beta);
- else
- %没找到这样的端点
- fa = fun(a);
- if fun(a) < fun(b)
- xk = a;
- else
- xk = b;
- end
- xlog = xk;
- end
- end
- end
- function [xk xlog] = Bisection(a, b, epsil, maxIt, diff_fun, alpha, beta)
- % 标准二分法
- k = 0;
- while k <= maxIt
- xk = alpha * a + beta * b;
- diff_fx = double(diff_fun(xk));
- if diff_fx < 0
- a = xk;
- else
- b = xk;
- end
- k = k + 1;
- xlog(k) = xk;
- if abs(diff_fx) < epsil
- break;
- end
- if abs(a-b) < epsil
- break;
- end
- end
- end
测试结果
- syms f(x)
- f(x) = sin(x) + cos(x)-0.1*x;
- bifact = 0.5
- maxIt = 1000;
- epsil = 0.001;
- x = 0:0.01:10;
- plot(x,double(f(x)));
- hold on
- a = 2
- b = 6
- [xk xlog] = BisectionInt(f, a, b, epsil, maxIt, bifact)
- scatter(xk, double(f(xk)))
- hold on
- a = 0
- b = 2
- [xk xlog] = BisectionInt(f, a, b, epsil, maxIt, bifact)
- scatter(xk, double(f(xk)))
- hold on
- a = 2
- b = 8
- [xk xlog] = BisectionInt(f, a, b, epsil, maxIt, bifact)
- scatter(xk, double(f(xk)))
- hold off
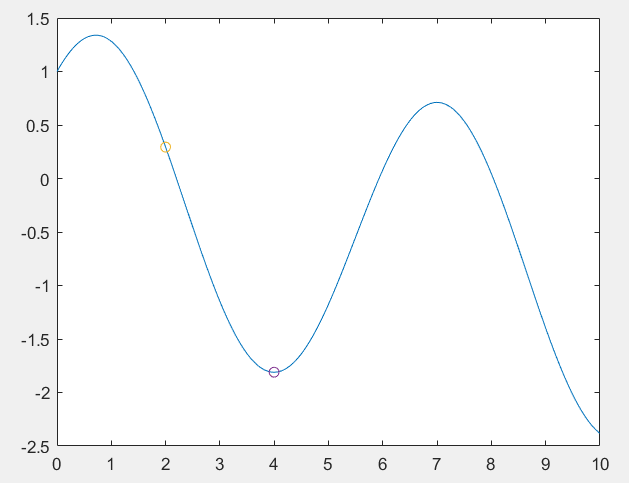
如果函数复杂,比如分段函数,那么直接使用diff符号求导可能不合适,则需要使用diff的数值求导.
*可以看到二分法并不简单啊~~
2. 成功-失败法
二分法要求函数可导,而成功失败发不要求初始区间和目标函数可导性,其算法格式如下
算法 2 成功-失败法
Step 1. 给定初始点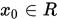 , 搜索步长
, 搜索步长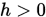 , 计算精度
, 计算精度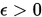 , 置
, 置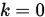 .
.
Step 2. 令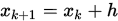 , 计算
, 计算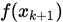 . 若
. 若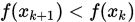 , 则称探索成功,
, 则称探索成功, 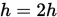 . 若
. 若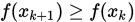 , 则称探索失败,
, 则称探索失败,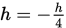 , 且
, 且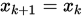 , 转下步.
, 转下步.
Step 3. 检验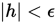 , 若成立,则
, 若成立,则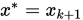 , 否则
, 否则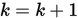 转 Step 3.
转 Step 3.
算法中标红部分是书中没有写的,若没有这一步骤算法将会周期震荡。
代码如下
- % 一维最优化问题的二分搜索
- % fun 目标函数, 可以是符号函数或函数句柄
- % epsil 指定终止条件(精度)
- % maxIt 最大迭代次数
- function [xk xlog] = SuccFa(fun, x0, h, epsil, maxIt)
- if ~isa(fun,'function_handle')
- fun = matlabFunction(fun);
- end
- k = 0;
- xlog = x0;
- while k <= maxIt
- xk = x0 + h;
- if fun(xk) < fun(x0)
- h = 2 * h;
- x0 = xk; %如果这一行放在判断之后,则不收敛
- else
- h = - h / 4;
- end
- k = k + 1;
- xlog(k) = xk;
- if abs(h) < epsil
- break
- end
- end
- end
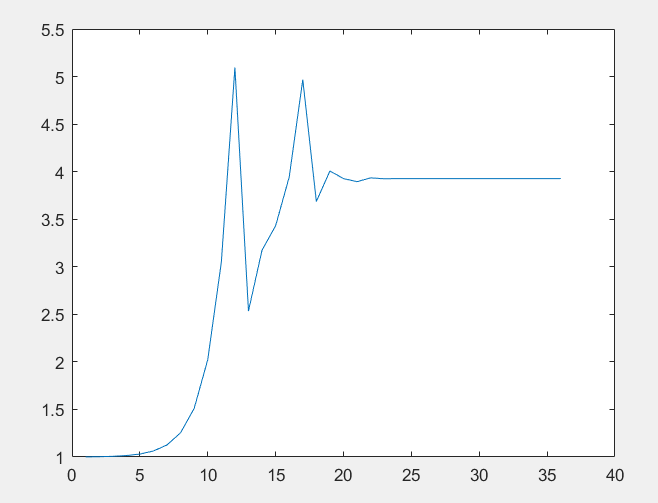
测试结果
- syms f(x)
- f(x) = sin(x) + cos(x);
- tf = matlabFunction(f);
- [xk xlog] = SuccFa(f, 1, 0.001, 1e-7, 1e4);
- plot(xlog)
- plot(0:0.01:10,tf(0:0.01:10))
如图所示

 浙公网安备 33010602011771号
浙公网安备 33010602011771号