2023-06-28《计算方法》- 陈丽娟 - 向量和矩阵基础.md
2023-06-28《计算方法》- 陈丽娟 - 向量和矩阵基础
本问补充向量和矩阵范数的相关知识,为下一章节的线性方程组的迭代法以及误差分析做准备。除了参考《计算方法》一书,还参考了华东师范大学数学学院的课程材料《迭代方法与预处理》以及陈新宇、伍元凯、赵熙乐和孙立君所著《面向时空交通数据修复及预测的低秩机器学习模型》, 有兴趣者可以去看他们在Github发布的文章 https://xinychen.github.io/books/spatiotemporal_low_rank_models.pdf
1. 向量范数
定义1:
设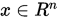 , 实值函数
, 实值函数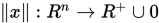 称
称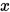 的范数,如果
的范数,如果
- 非负性;
- 齐次性:即
![]() ,
, ![]() ;
; - 三角不等式:对任意两个向量
![]() , 都有
, 都有
![]()
向量范数所表示即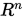 中的一个度量,表示向量的长度,下面给出向量范数的几个例子:
中的一个度量,表示向量的长度,下面给出向量范数的几个例子:
- 1-范数:
![]() ;
; - 2-范数:
![]() ;
; ![]() -范数:
-范数:![]() ;
;- p-范数:
![]() ,
, ![]() ;
;
需要注意向量0-范数(计数)不满足向量范数的定义。另外向量和内积有以下关系:
推论1:
设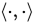 是
是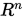 上的内积,则
上的内积,则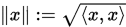 是
是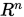 上的一个向量范数。
上的一个向量范数。
既然在 中的向量范数有无穷多个定义,那么我们该如何选择使用哪个范数呢?下面的定理将告诉我们虽然向量范数有无穷多个,但是任意两个向量范数之间是等价的。
中的向量范数有无穷多个定义,那么我们该如何选择使用哪个范数呢?下面的定理将告诉我们虽然向量范数有无穷多个,但是任意两个向量范数之间是等价的。
定理1:
在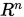 上定义的任一向量范数都与向量1-范数等价,即存在正数
上定义的任一向量范数都与向量1-范数等价,即存在正数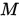 和
和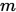 ,
, 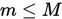 对一切
对一切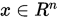 , 下述不等式成立:
, 下述不等式成立:
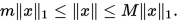
按照书中的方式给出证明:
设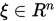 , 由三角不等式可知
, 由三角不等式可知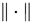 是连续函数,则
是连续函数,则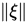 在单位球面
在单位球面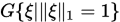 上有界。设其最大值为
上有界。设其最大值为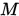 , 最小值为
, 最小值为 ,则有
,则有
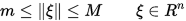
另设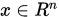 为任意非零向量,则
为任意非零向量,则
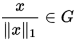
(即变为单位向量),然后即得
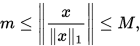
也即是
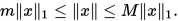
虽然定理1只说明任意向量范数都与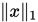 范数等价,但是很容易就能得出对于任意
范数等价,但是很容易就能得出对于任意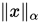 和
和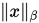 都是等价的,特别的:
都是等价的,特别的:
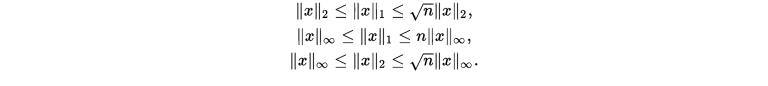
更广义的,
定理2:
有限维赋范线性空间上的所有范数都是等价的。
Cauchy-Schwartz 不等式
设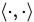 是
是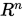 上的内积,则对任意
上的内积,则对任意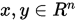 , 有
, 有
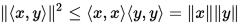
且等号成立的充要条件是
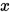 和
和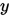 线性相关。
线性相关。
Holder 不等式
设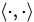 是
是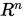 上的Euclidean内积, 则对任意
上的Euclidean内积, 则对任意 , 有
, 有
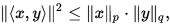
其中
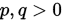 且
且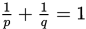 .
.
备注
关于p-范数是范数,Cauchy-Schwartz 不等式,Holder 不等式的证明可以在《矩阵理论》-黄廷祝 上找到。
2. 矩阵范数
矩阵范数的定义和向量范数如出一辙:
定义2:
设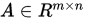 , 实值函数
, 实值函数 称
称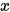 的范数,如果
的范数,如果
- 非负性;
- 齐次性:即
![]() ,
, ![]() ;
; - 三角不等式:对任意两个向量
![]() , 都有
, 都有
![]()
- 相容性:
![]() , for all
, for all ![]() .
.
后续叙述均在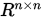 上讨论。
上讨论。
下面给出几个常见的矩阵范数:
![]() -范数
-范数
![]()
![]() -范数 (算子范数,诱导范数,导出范数)
-范数 (算子范数,诱导范数,导出范数)
![]()
- 1-范数(列范数):
![]() ;
; ![]() -范数(行范数):
-范数(行范数):![]() ;
;- 2-范数(谱范数):
![]() ,其中
,其中![]() 为
为![]() 的谱半径,
的谱半径,![]() 为
为![]() 的特征值
的特征值
简单计算即可验证 -范数不是算子范数(找不到这样的
-范数不是算子范数(找不到这样的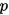 )
)
定理
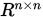 上的所有范数都是等价的,特别地
上的所有范数都是等价的,特别地
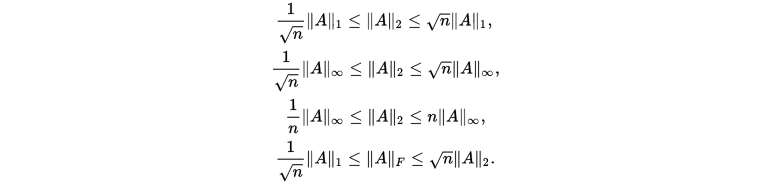
引理
设
 , 则
, 则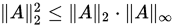 , 且
, 且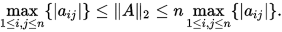
矩阵范数的性质(对复数域成立)
1. 对任意相容范数有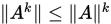 (由相容性定义可得);
(由相容性定义可得);
2. 任意算子范数都是相容范数;
3. 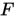 -范数是相容范数;
-范数是相容范数;
4. 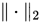 和
和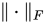 是酉不变范数,即对任意酉矩阵
是酉不变范数,即对任意酉矩阵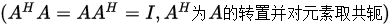
 ,有
,有
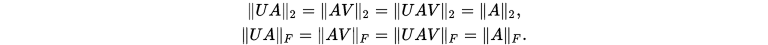
5.
 ,
, 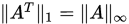
6. 若
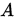 是正规矩阵
是正规矩阵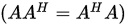 , 则
, 则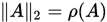 ,因此
,因此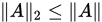 , 其中
, 其中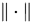 是任意算子范数。(
是任意算子范数。(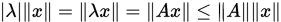 ,即
,即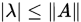 .)
.)
相应的结论可以退化到实数域中。
3. 病态矩阵
所谓病态矩阵即在线性方程组的求解过程中的舍入误差对求解会产生严重影响的一类系数矩阵。为了方便判断矩阵是否是病态的,给出条件数的定义:
定义
设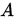 为
为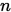 阶非奇异矩阵,则称数
阶非奇异矩阵,则称数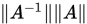 为矩阵
为矩阵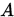 的条件数,记为
的条件数,记为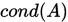 , 其具有性质
, 其具有性质
1.  ;
;
2. 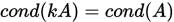 ,
, 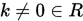 ;
;
3. 若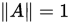 ,则
,则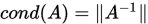 .
.
由于条件数的计算涉及矩阵求逆,因此实际上难以实现,如何对条件数进行合理估计在《矩阵理论》一书中有所涉及。下面按照《计算方法》给出一些经验判据:
1. 用列主元高斯消元法时,出现绝对值很小的主元素;
2. 系数矩阵行列式的绝对值很小或很大;
3. 系数矩阵元素的量级差别很大;
4. 系数矩阵的行列式几乎线性相关。
定理
设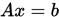 ,
, 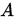 为非奇异矩阵,
为非奇异矩阵,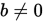 ,
,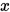 为方程组的精确解,
为方程组的精确解, 为求得的近似解,其剩余向量为
为求得的近似解,其剩余向量为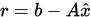 , 则有误差估计
, 则有误差估计
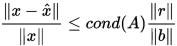
证明: 由
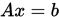 , 得到
, 得到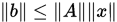 , 即
, 即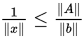 , 则有
, 则有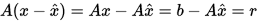
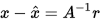
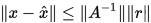
因此
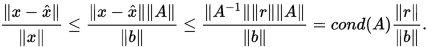
4. 向量和矩阵(含范数)导数
向量函数的导数即是多元函数的导数,其中相关的梯度和黑塞矩阵相关知识相同。
例 写出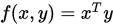 的偏导数
的偏导数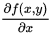 和
和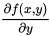 .
.
由于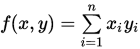 , 故
, 故
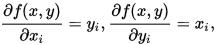
从而
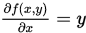 ,
, 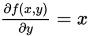 .
.
例 写出 的偏导数
的偏导数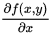 和
和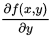 .
.
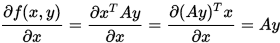
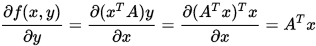
例 写出函数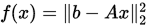 的导数。
的导数。
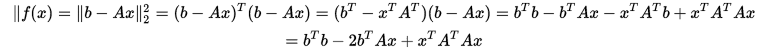
其中
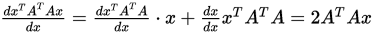
则
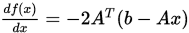 .
.


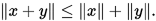
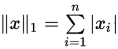
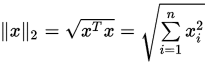
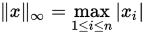
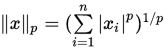
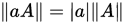
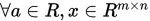
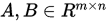

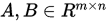
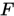
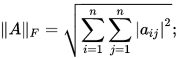
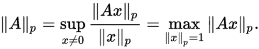
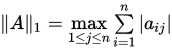

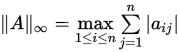
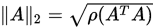
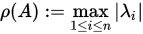


 浙公网安备 33010602011771号
浙公网安备 33010602011771号