卡常小技巧

那些也许有用的卡常小技巧

作者卡Ynoi卡吐了

一，代码优化

1.inline

其实还是有点用的。
不带inline:

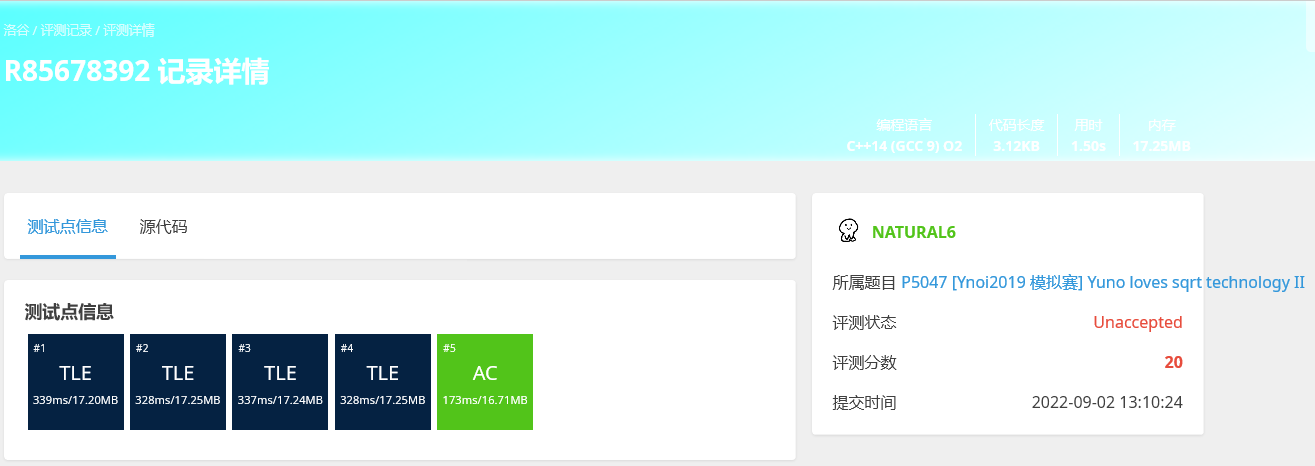
带inline:

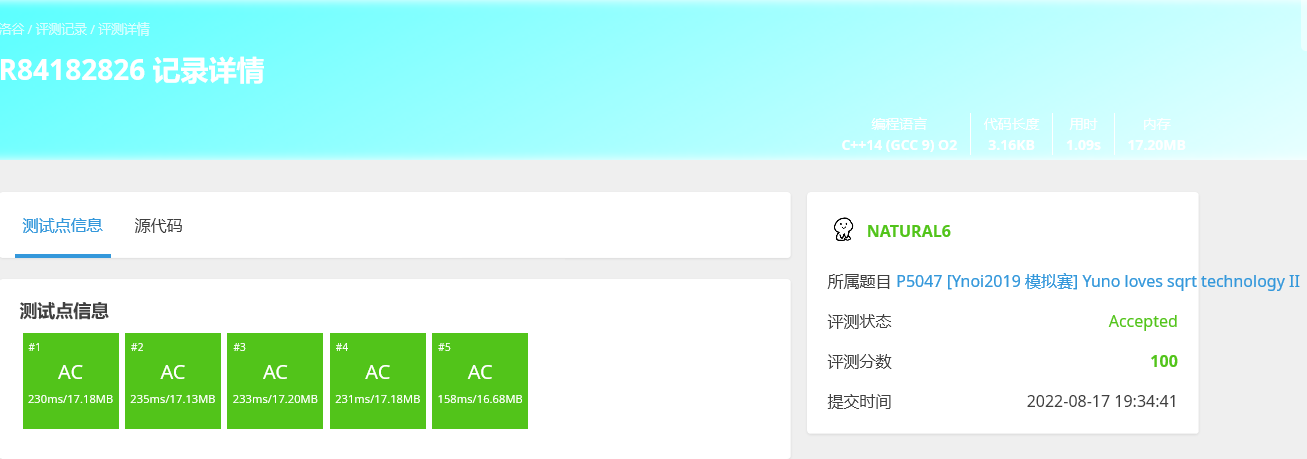
2.register

注意有些不能加，但优化程度还是很大的。
不带register:

带register:

3.i++ $ \Rightarrow $ ++i

但是优化很小，如果只差一点可以加上后多跑几遍，增大卡过的概率
i++:

++i:

4.强制转型

(ll)x是很慢的，1llx要快很多，同样的还有(double)x和1.0x。

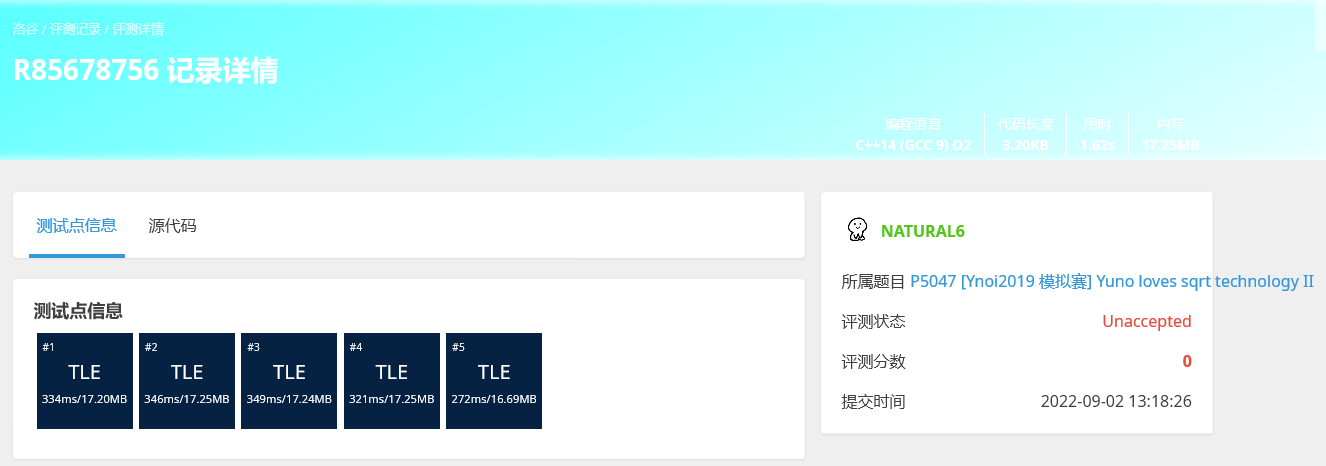
5.unsigned

加上一个unsigned会比不加快很多
没加：

加了:

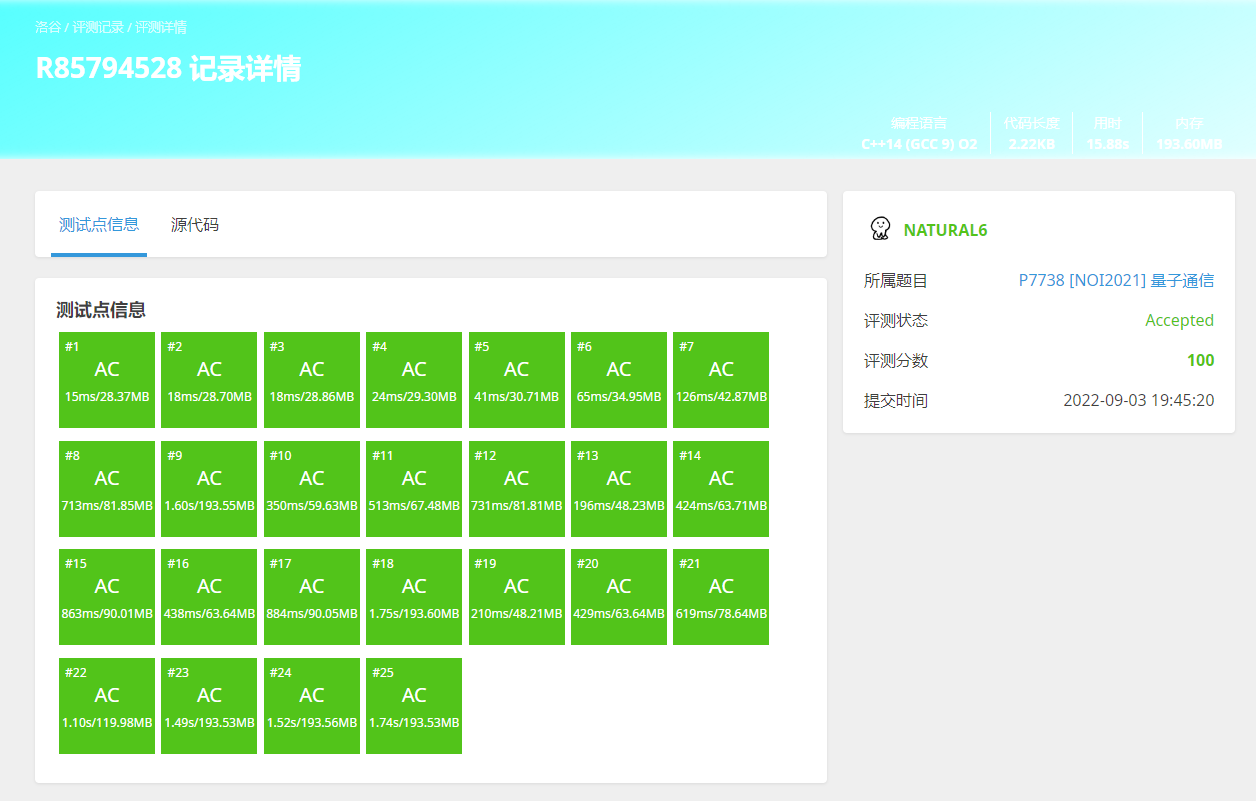
6.memcpy

这个东西比for快不知道多少倍，用法和memset类似

二，算法优化

7.基数排序

鸡排是很优秀的桶排，可以把空间优化到 \(O(\sqrt{n})\) 的同时保持 \(O(n)\) 的时间复杂度。但在数据小或比较有序时可能不如sort
取一个值T,先将数据按 $a_i \bmod T $ 入桶，再按 $ \frac{a_i}{T} $ 入桶即可。
代码实现：

n=qread();
for(register int i=1;i<=n;++i)
{
	a[i]=qread();
	mx=max(mx,a[i]);
}
cl=sqrt(mx)+1;
for(register int i=1;i<=n;++i)
{
	mx=a[i]%cl;
	v[mx].push_back(a[i]);
	++vl[mx];
}
for(register int i=0;i<cl;++i)
{
		for(register int j=0;j<vl[i];++j)
		{
			a[++p]=v[i][j];
		}
		vl[i]=0;
		v[i].clear();
	}
	for(register int i=1;i<=n;++i)
	{
		mx=a[i]/cl;
		v[mx].push_back(a[i]);
		++vl[mx];
	}
	p=0;
	for(register int i=0;i<=cl+1;++i)
	{
		for(register int j=0;j<vl[i];++j)
		{
			a[++p]=v[i][j];
		}
	}
	for(register int i=1;i<=n;++i)cout<<a[i]<<" ";
}

8.%优化

<1>

对于一般的要求%的题目，两个数相加后不会超过两倍模数，所以可以if判是否大于后再减，会比%快不少。
对于超过两倍模数的时候，如果是统计答案，全程加/乘的是同一个数，那么可以将那一个数开成long long 后最后再取模，一般会比int不停取模要快一些。
直接取模：

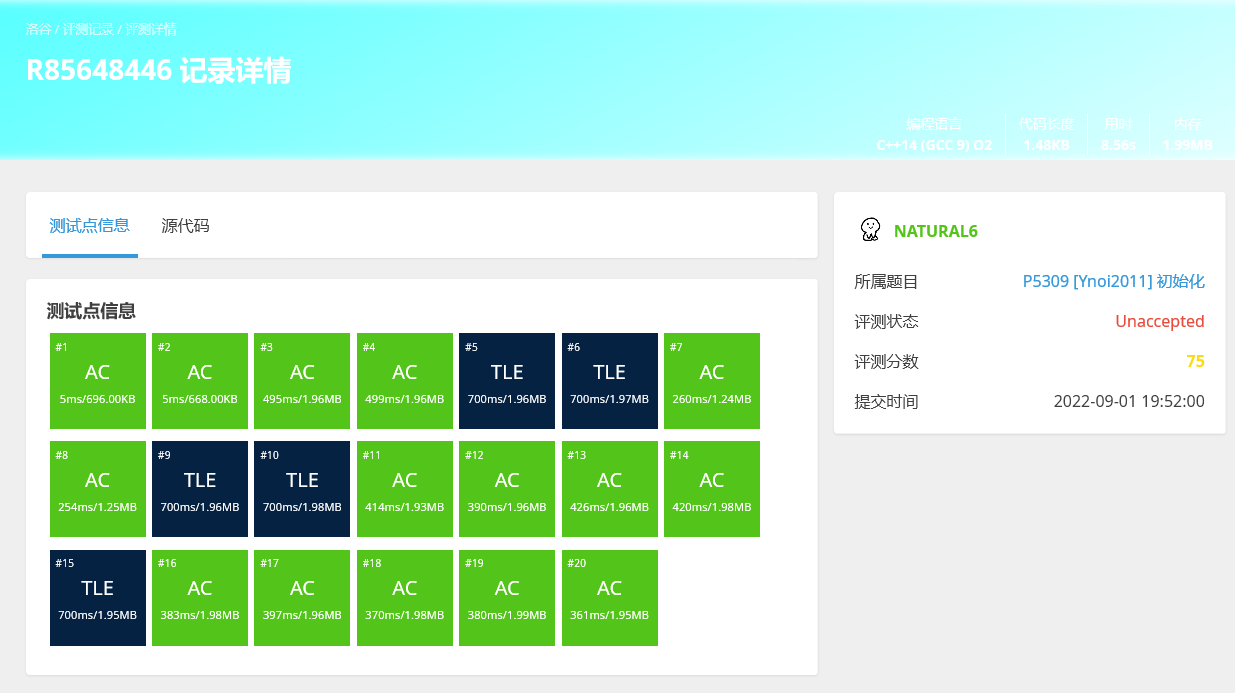
两个优化都加：

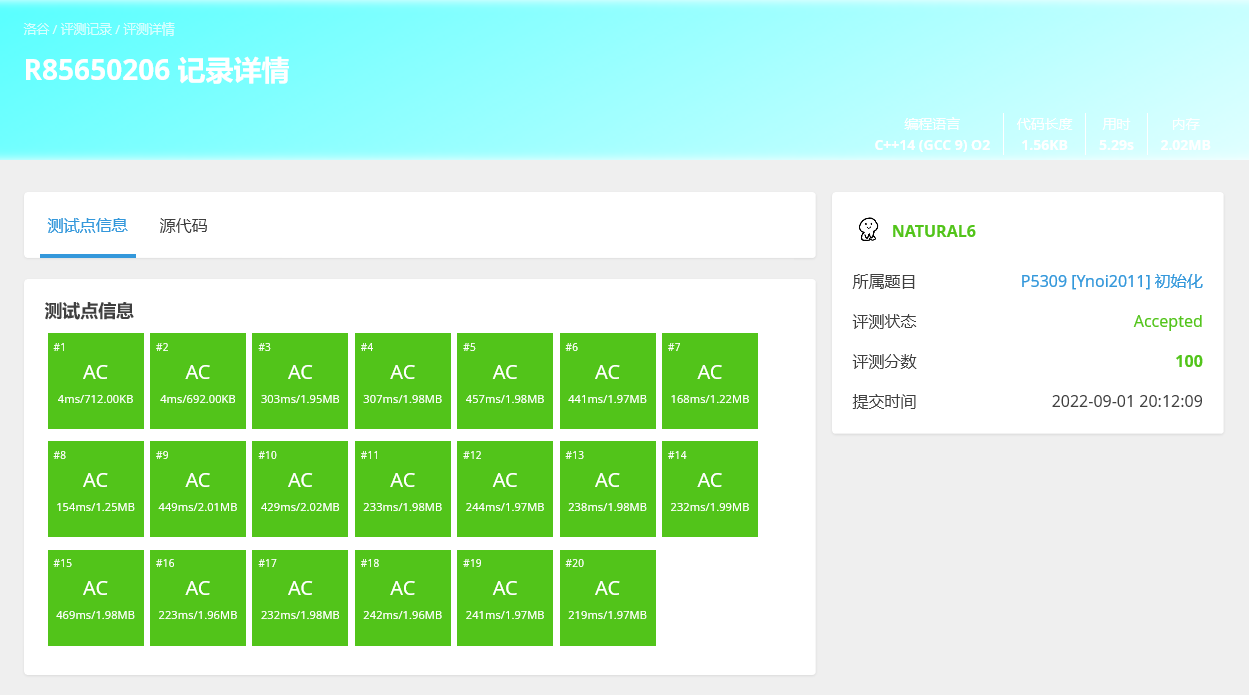
<2>

还有对于%数是自己定的时候，%数取到\(2^x-1\)时可用&优化，比取模要快很多。

<3>

然后就是比较高级的啦。
首先对于%运算，我们可以把它拆成一次除法，一次乘法，一次减法，乘和减的常数较小，但除法很大，所以这是负优化。
我们考虑怎么优化除法，我们很快可以想到，位运算的>>是很快的，如果我们能把除法变成>>的话，常数将大大减小。
怎么做呢？
可以先处理出一个数B，B=\(\frac{2^{64}}{mod}\),用x先乘上B在>>64即可得到x/mod，剩下就好办了。
代码实现：

struct fastmod {
  typedef unsigned long long u64;
  typedef __uint128_t u128;

  int m;
  u64 b;

  fastmod(int m) : m(m), b(((u128)1 << 64) / m) {}
  int reduce(u64 a) {
    u64 q = ((u128)a * b) >> 64;
    int r = a - q * m;
    return r < m ? r : r - m;
  }
} z(2);

9.gcd优化

一般gcd时间复杂度是 \(O(log_n)\) 的，这显然太慢了，我们可以把它优化到 \(O(能过)\)。
新算法
设现在要计算a和b两数的gcd。
若a和b都是偶数，则递归计算 \(2 \times gcd(\frac{a}{2},\frac{b}{2})\)。
若a是偶数，且b是奇数，则递归计算 \(gcd(\frac{a}{2},b)\) 。
若a是奇数，b是偶数同理。
若a和b都是奇数，则递归计算 \(gcd(|a-b|,a)\)。
这样就会比辗转相除快了。
代码实现：

inline int gcd(int x,int y)
{
	if(!x) return y;
	if(!y) return x;
	int t=__builtin_ctzll(x|y);
	x>>=__builtin_ctzll(x);
	do
	{
		y>>=__builtin_ctzll(y);
		if(x>y) swap(x,y);
		y-=x;
	}while(y);
	return x<<t;
}

10.顺便介绍下builtin一家

__builtin_ctz(unsigned int x)
求x的二进制末尾有几个0。
__builtin_clz(unsigned int x)
求x的二进制有几个前导0。
__builtin_ffs(unsigned int x)
求x的二进制的末位1的位置。
__builtin_popcount(unsigned int x)
求x的二进制中1的个数。
__builtin_parity(unsigned int x)
求上一个的奇偶。

11.除优化

优化方式用取模优化<3>差不多。

对于 \(b\) 为奇数，预处理出 \(b\mod 2^k\) 下的逆元和 \(r=\left\lfloor\dfrac{2^k}{b}\right\rfloor\),则有 \(\dfrac{a}{b}=a*b^{-1}\mod 2^k\) ,只需要一次乘法和一次比较。据测试，此做法比通常计算常数会优化 \(8\sim 10\) 倍。

对于当 \(b\) 为偶数时，可以令 \(b=b_02^k\) ,将该除法转化为一次按位与+一次右移+一次乘法+一次比较。

由于大于 2 的质数全为奇数，所以该做法可以很好地适用质因数分解等算法。

12.线段树优化

在跑线段树的时候，我们会发现，在最底层线段树，会进行很多次递归操作。

而因为底层线段树节点长度有限，函数递归常数又很大，这并不能跑出优秀的效率。

于是我们可以将底层节点删除，保留到长度为 \(\log{n}\) 的那层，下面的直接for循环，减少递归层数。

这样常数就小多了，并且线段树层数也变成了 \(\log n-\log\log n\) 层。

然后我们发现线段树最上端的节点也没什么用，往往只是用来下传操作的。

于是我们可以将线段树最上层的这些节点删去，换成块长为 \(\dfrac{n}{\log n}\) 的分块。

这样上端总共 \(\log n\) 块，操作时直接for一遍即可，常数比递归小，线段树的层数也减少了 \(\log\log n\) 层。

可以看到，在这两个优化同时加上时，线段树的层数少了约一半，时空都会优化很多。