理解Liang-Barsky裁剪算法的算法原理

0.补充知识
向量点积:结果等于0, 两向量垂直; 结果大于0, 两向量夹角小于90度; 结果小于0, 两向量夹角大于90度.
直线的参数方程:(x1, y1)和(x2, y2)两点确定的直线, 其参数方程为x = x1+u(x2-x2); y = y1+u(y2-y1)

1.前言
Liang-Barsky算法是 Cyrus-Beck 算法的特例, 我们先来简单的了解Cyrus-Beck算法, Cyrus-Beck算法本质是每次通过裁剪窗口(任意凸多边形, 文章最后会说明为什么凹多边形不行)的一条边界来确定待裁剪线段的哪部分应当被留下, 最后, 对所有应该被留下的部分取交集, 便可以求得线段应当留下的部分.举个例子, 假设多边形ABCDE, 那么我们每次使用一条边(AB, BC, …), 延长这条边和待裁剪的线段, 那么最后两条直线必定相交或平行, 如果相交, 根据交点确定哪部分被留下, 如果平行, 根据坐标确定哪部分被留下. 而Liang-Barsky算法只是将这个裁剪窗口固定为了一个平行于坐标轴的矩形, 所以Liang-Barsky算法和Cyrus-Beck算法本质是一样的, 只是Liang-Barskys算法因为拥有更多信息(裁剪窗口是一个平行与坐标轴的矩形), 可以对其中一些步骤进行简化处理.

 

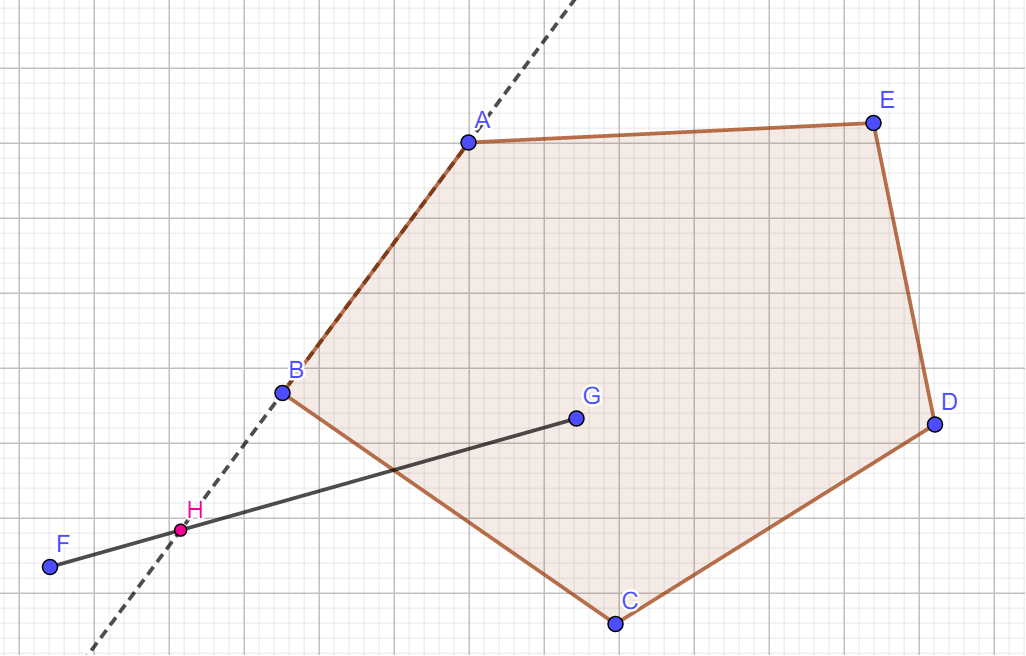
2.对于一条边界, 具体如何确定线段应当留下的部分?

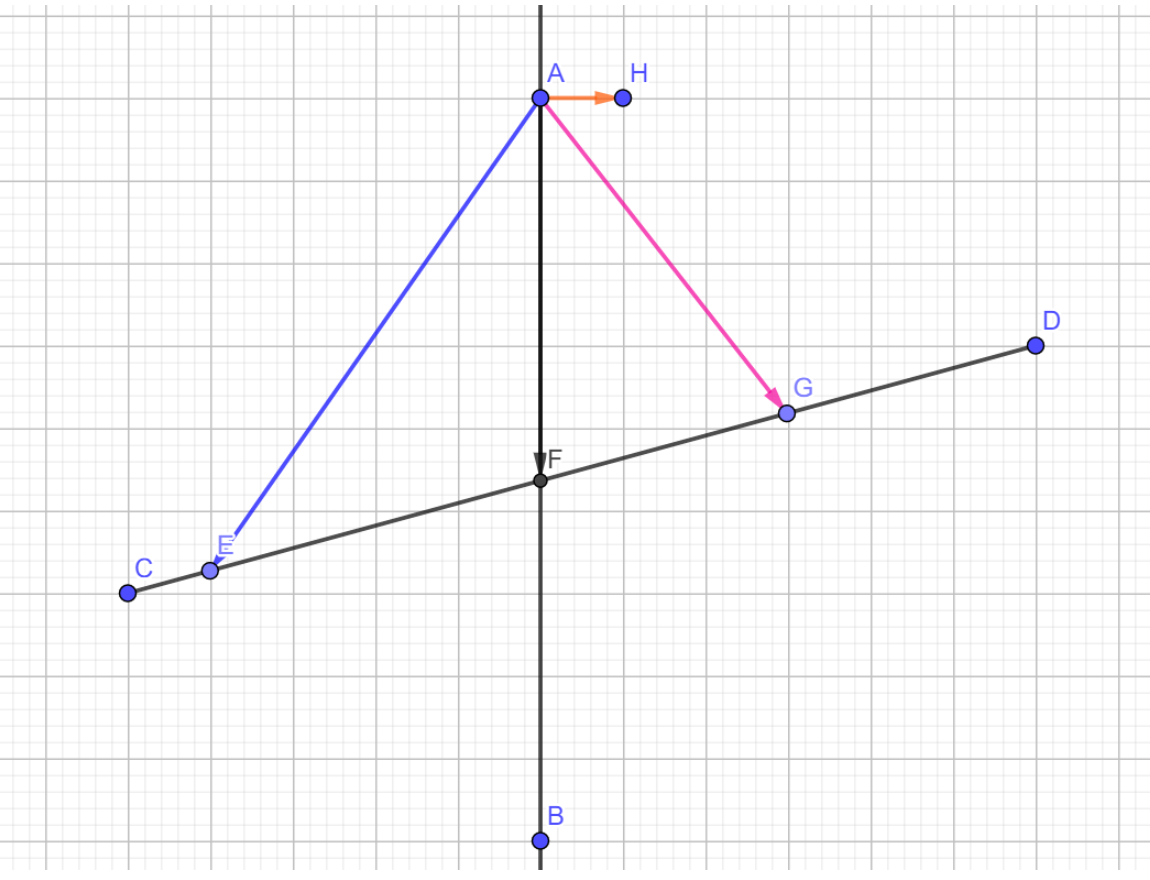
2.1符号说明
AB:边界直线, 把整个平面划分为两部分, 我们约定向量AH所在区域称为内部区域, 另一部分称为外部区域
AH:边界直线的法向量, AH=(1,0)
CD:待裁剪线段,C(x1, y1), D(x2, y2),CD的向量表示为 (x1+u(x2-x1), y1+u(y2-y1))(0<=u<=1)
E,F,G:待裁剪线段上三点

2.2判定方法
向量AH*向量AG, 结果大于0, H点处于内部区域
向量AH*向量AF, 结果等于于0, F点位于边界上
向量AH*向量AE, 结果小于0, E点处于外部区域
所以, 通过AX(X为线段CD上任意一点)与法向量AH的乘积即可判定X点位于内部区域还是外部区域

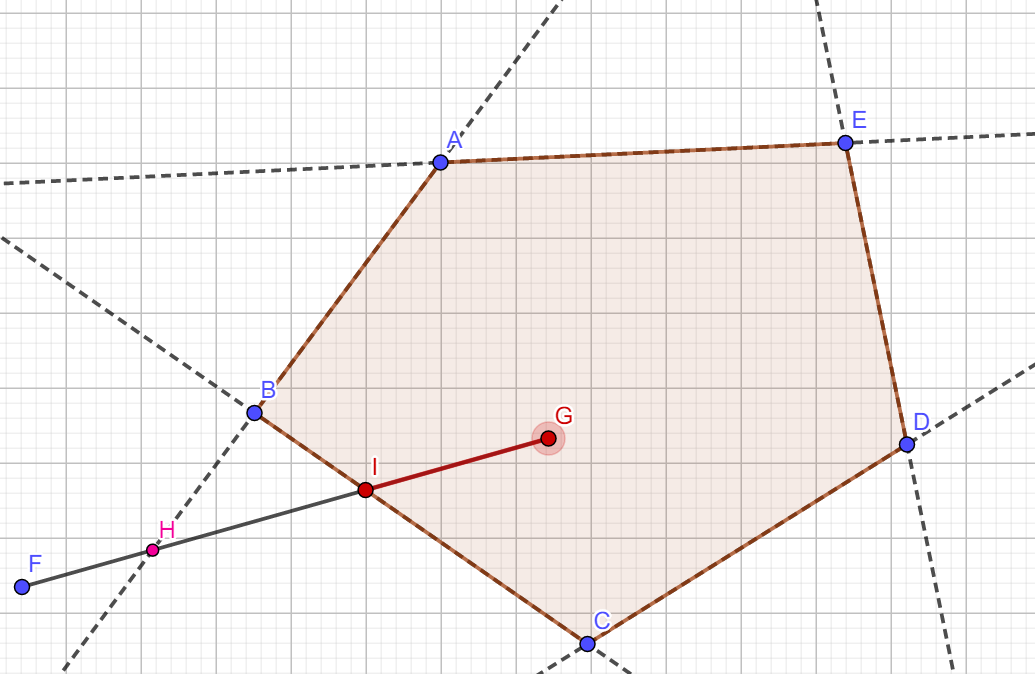
3.对于任意凸多边形边界, 如何确定线段应当留下的部分?
任意凸多边形边界和直线边界没有本质区别, 如果对于矩形上的所有边, 点X都满足属于这条边的内部区域, 那么X就在矩形的内部区域.(比如图中的IG部分)

 4.Liang-Barsky的算法流程以及算法中的p和q

4.1算法流程

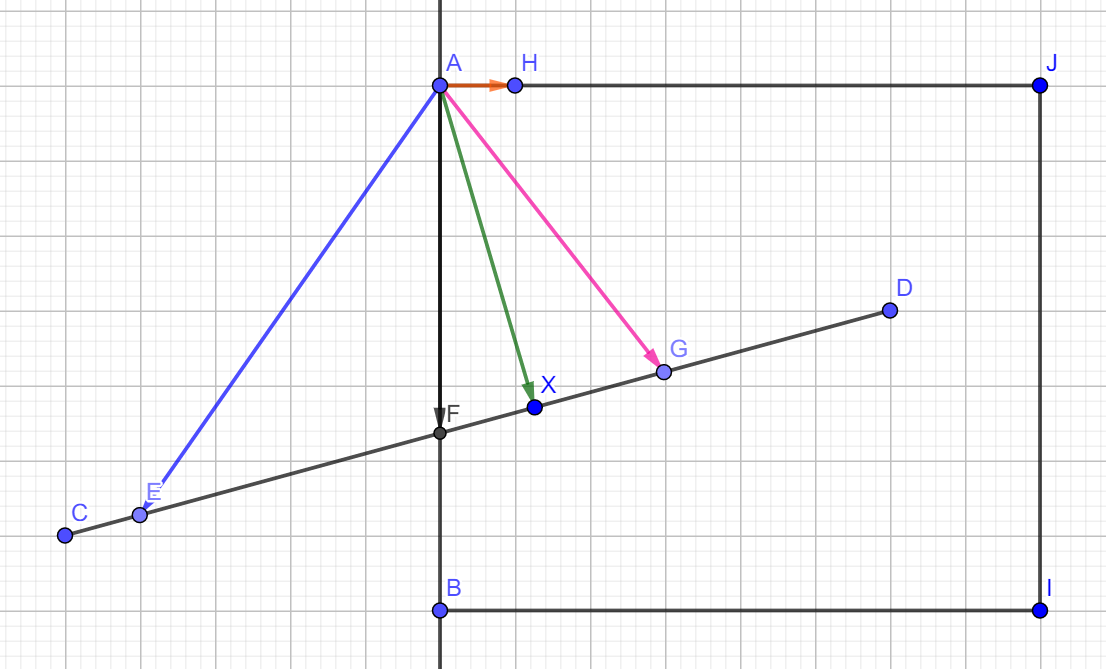
以AB边为例, X为CD上任意一点, 矩形边界的左右上下边界分别为XL, XR, YT, YB
因为向量AH*向量AX>=0时, X点在AB的内部区域
所以我们现在求解这个不等式:
向量AH*向量AX>=0
向量AH*(向量OX-向量OA)>=0;
由CD的向量表示式可知
(1,0)*(x1+u(x2-x1)-XL, y1+u(y2-y1)-YA)>=0;(我们不用关心YA的具体值, 请不要在此纠结)
x1+u(x2-x1)-XL>=0;
假设x2-x1>0(图中是大于0, 但是对于任意直线, 可能大于0, 小于0, 等于0)
则u>=(XL-x1)/(x2-x1)时, 点X在直线AB的内部区域
假设x1-x2<0
则u<=(XL-x1)/(X2-X1)时, 点X在直线AB的内部区域
如果x2-x1=0,则简单判断x1和XL的大小, 如果x1<XL, 舍去, 否则保留
本步执行完后, 我们得到一个关于u的不等式

同理对矩形另外三条边做如上处理, 我们得到另外3个不等式
我们现在观察一下这四个不等式
因为AB边和IJ边的法向量x坐标值为-1和1
那么如果AB边算出的不等式是u>=(XL-x1)/(x2-x1), 则IJ边算出来一定是u<=(XR-x1)/(x2-x1)(因为IJ边计算时仅仅是把XL换成XR, 1换成-1, 不理解请自己按照上述步骤计算一下), 我们可以发现, 互相平行的两条边算出来的不等式一个是>=那么另一个一定是<=(其实就是一维裁剪, 确定线段的上限和下限).
那么对4条边分别进行如上处理, 会得到u<=ans1, u<=ans2, u>=ans3, u>=ans4这4个不等式
ans1,ans2为u可能的上限, ans3,ans4为u可能的下限
又因为参数方程实际上是表示一条直线, 而我们需要裁剪的是一条线段, 所以u应当在0和1之间
于是
令umax = min(ans1, ans2, 1);//因为是取交集, 所以我们应在可能的上限中取最小的那个
umin = max(ans3, ans4, 0);
如果umax<umin则没有线段位于裁剪窗口的内部
否则将参数u带进参数方程, 求得裁剪之后线段的两个端点
最后利用端点画出裁剪结果即可

4.2算法中的p和q
L, R, T, B是对应边上的一点
(1,0)*(x1+u(x2-x1)-XL, YL) >=0;
(-1,0)*(x1+u(x2-x1)-XR, YR) >=0;
(0,1)*(XB, y1+u(y2-y1)-YB) >=0;
(0,-1)*(XT, y1+u(y2-y1)-YT) >=0;
令p1 = -(x2 - x1); p2 = -p1
p3 = -(y2 - y1); p4 = -p3
上面的不等式变为
x1+u*p2-XL>=0;
-x1+u*p1+XR>=0;
y1+u*p4-YB>=0;
-y1+u*p3+YT>=0;
移项
u*p2>=XL-x1;
u*p1>=x1-XR;
u*p4>=YB-y1;
u*p3>=y1-YT;
同时乘上-1(为了让不等式组看起来有序)
u*p1<=x1-XL;
u*p2<=XR-x1;
u*p3<=y1-YB;
u*p4<=YT-y1;
令q1 = x1-XL;
...
q4 = YT-y1;
假设p1<0, p3<0
u>=q1/p1
u>=q3/p3
u<=...
u<=...
不等式取交集即可得到u的范围, 可以看到p和q并没有明显的物理意义, 请不要纠结于此
5.Liang-Barsky的c++代码实现

void LiangBarsky(int x1, int y1, int x2, int y2, int XL, int XR, int YT, int YB)
{
    int ansx1, ansx2, ansy1, ansy2;
    //三种类型
        //平行于y轴
    if (x1 - x2 == 0)
    {
        if (x1<XL || x1>XR)
        {
            return;
        }
        else
        {
            int ymin = max(YB, min(y1, y2));
            int ymax = min(YT, max(y1, y2));
            if (ymin <= ymax)
            {
                ansx1 = ansx2 = x1;
                ansy1 = ymin;
                ansy2 = ymax;
            }
            else
            {
                return;
            }
        }
    }
        //平行于x轴
    else if (y1 - y2 == 0)
    {
        if (y1<YB || y1>YT)
        {
            return;
        }
        else
        {
            int xmin = max(XL, min(x1, x2));
            int xmax = min(XR, max(x1, x2));
            if (xmin <= xmax)
            {
                ansy1 = ansy2 = y1;
                ansx1 = xmin;
                ansx2 = xmax;
            }
            else
            {
                return;
            }
        }
    }
        //不平行于坐标轴
    else
    {
        float p1, p2, p3, p4;
        float q1, q2, q3, q4;
        p1 = -(x2 - x1);
        p2 = -p1;
        p3 = -(y2 - y1);
        p4 = -p3;
        q1 = x1 - XL;
        q2 = XR - x1;
        q3 = y1 - YB;
        q4 = YT - y1;
        float u1, u2, u3, u4;
        u1 = q1 / p1;
        u2 = q2 / p2;
        u3 = q3 / p3;
        u4 = q4 / p4;
        float umin, umax;
        if (p1 < 0)
        {
            if (p3 < 0)
            {
                umin = max(0, max(u1, u3));
                umax = min(1, min(u2, u4));
            }
            else
            {
                umin = max(0, max(u1, u4));
                umax = min(1, min(u2, u3));
            }

        }
        else
        {
            if (p3 < 0)
            {
                umin = max(0, max(u2, u3));
                umax = min(1, min(u1, u4));
            }
            else
            {
                umin = max(0, max(u2, u4));
                umax = min(1, min(u1, u3));

            }

        }
        if (umin <= umax)
        {
            ansx1 = x1 + umin * (x2 - x1);
            ansx2 = x1 + umax * (x2 - x1);
            ansy1 = y1 + umin * (y2 - y1);
            ansy2 = y1 + umax * (y2 - y1);
        }
        else
            return;
    }
    //调用函数重绘直线
        YourDrawFunc();
    return;
}

 

6.教材上的算法流程和解题实例
相信有了上面的基础, 再回头看书上对于Liang-Barsky算法的讲解, 就不会一头雾水了.
相关内容在这篇博文中已经写的很清楚了, 故本文不在赘述.
[计算机图形学经典算法] Liang-Barsky（梁友栋-Barsky） 算法 （附Matlab代码）: https://blog.csdn.net/soulmeetliang/article/details/79185603

7.从Liang-Barsky算法到Cyrus-Beck算法
7.1为什么凹多边形无法使用Cyrus-Beck算法?

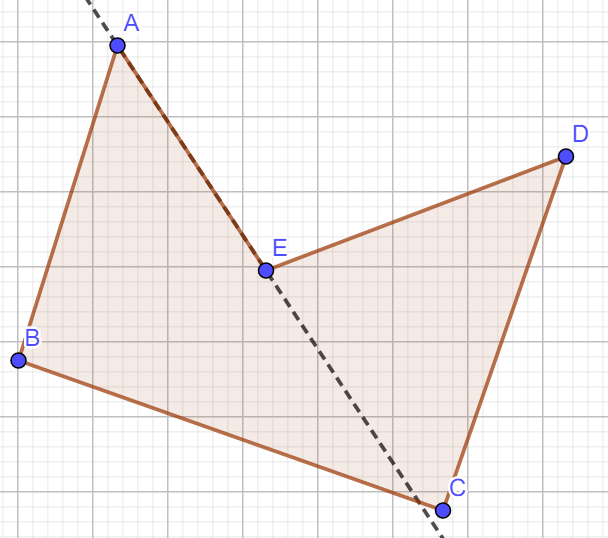
因为凹多边形的边界不一定保证把平面区域分成多边形内部和外部两个区域

7.2Cyrus-Beck算法如何求得边界法向量?
Liang-Barsky算法因为裁剪窗口得特殊性, 每条边界得法向量我们作为已知量来处理. Cyrus-Beck中需要自己确定法向量, 思路如下: 根据边界(假定为AB)确定垂直于边界的法向量(a1, a2), 任取多边形除了本次边界上两点之外的任意一点P, 计算向量AP(BP)*a1, 大于0取a1, 否则取a2

7.3u的上下限对应关系
Liang-Barsky算法中, 我们知道平行的两条边一条提供上限则另一条提供下限. 对于更一般的凸多边形裁剪窗口, 则是与线段延长线相交的两条边界延长线对应的边界. 从不等式来看, xi+u*(xj-xi)中的(xj-xi)决定了得到u的上限还是下限, 可以据此实现上下限的区分.

8.参考资料

 [计算机图形学经典算法] Liang-Barsky（梁友栋-Barsky） 算法 （附Matlab代码）: https://blog.csdn.net/soulmeetliang/article/details/79185603

理解梁友栋-Barsky裁剪算法: https://blog.csdn.net/Daisy__Ben/article/details/51941608

梁友栋-Barsky算法原理: http://www.voidcn.com/article/p-niexnvwo-rv.html

 

作者：kkbeta

出处：https://www.cnblogs.com/kkbeta/

版权所有，欢迎保留原文链接进行转载：)