CF1394

CF1394A Boboniu Chats with Du

洛谷链接

刚开始怎么看怎么像反悔贪心，但悔着悔着发现根本不用反悔。

枚举选取 \(k\) 个需要代价（大于 \(m\)）的数（显然选取最大的 \(k\) 个数最优），此时有 \((k-1)\times d\) 个数作为代价。那么肯定是先将所有未选取的大于 \(m\) 的数当成代价，再将较小的不需要代价的数作为代价。此时，还有 \(n-(k-1)\times (d+1)-1\) 个小于 \(m\) 的数可选，加入其中最大的若干个数即可

CF1394B Boboniu Walks on Graph

洛谷链接

题意即需要每个点保留一条出边后整个图是个环，其等价于每个点的入度都为 \(1\)。注意到 \(k\) 很小，所以我们容易想到枚举 \(9!\) 种方案后判断图是否合法。

显然我们可以预处理出每条边在什么情况下可以被保留下来，此时可以 \(O(k)\) 用哈希表示出每种方案的边集。但是边集是没用的 但是我们关心的是入度的集合，所以我们可以改为预处理求出入度集合的哈希值，再将其与 每个点作为入度一次 的哈希值比较。

CF1394C Boboniu and String

洛谷链接

好高级。

说到最大值最小那首先肯定想到二分，每次 check 判断每个字符串的操作次数不超过 \(mid\) 时是否可以构造出合法的 \(t\)

可以观察到，两个字符串合法当且仅当两个字符串中 B 与 N 的出现次数相同，而四种操作的本质即为分别加减 B N 的数量或同时加减 B N 的数量。在操作次数 \(mid\) 的限制下，每个字符串 \(s\) 的变化是有限定范围的，若可以构造 \(t\)，那一定是所有字符串的限制范围有交。

显然，我们无法用一维区间 \([l,r]\) 描述该限制，既然有两种不同字符，考虑用二维坐标 \((x,y)\) 描述限制。

对于一个字符串，将其 B 的出现次数看作第一维，N 的出现次数看作第二维，那么每个字符串都可以被一个坐标 \((x,y)\) 描述。每次操作即是在第一象限移动该点

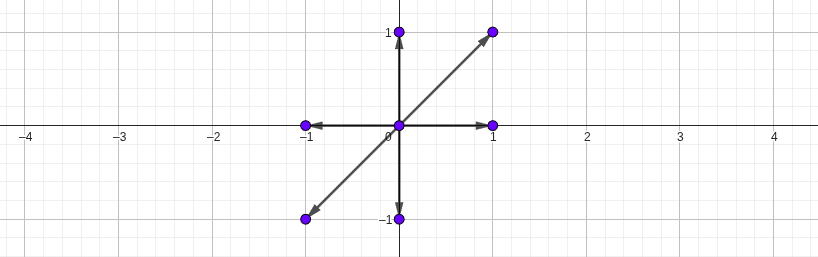
操作次数小于等于某值时，该点的合法位置构成的平面形状如下图

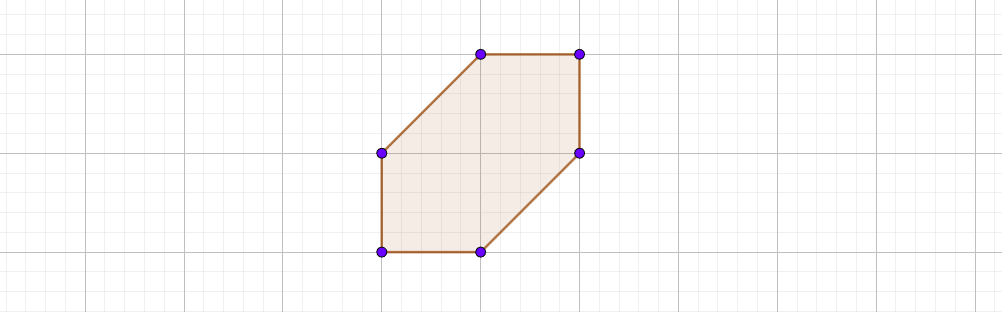
那么该限制就可以用六个不等式描述了

判断是否有交只需要分别判断三个区间是否合法、再判断平面是否与一次函数的范围有交即可