CF1442

A.Extreme Subtraction

洛谷链接& CF 链接

我们将前缀减操作与后缀减操作分离开来，显然，这两种操作减去的序列一个单调不升，一个单调不降，原序列就是这两个序列加起来得到的序列。考虑构造这两个序列，每一位都贪心考虑（第一个序列的值尽量大，第二个序列的值尽量小），若能构造成功那么一定有解

B.Identify the Operations

洛谷链接& CF 链接

结论题。

显然，若是删除 \(a_i\) 并将 \(a_{i-1}\) 添加至序列 \(b\)，那么 \(a_i\) 肯定不会在之后的 \(b\) 序列中出现；同理，\(b_i\) 的两个可能被删的值 \(a',a''\)，一定不会出现在 \(b_i\) 之后。所以在顺序遍历 \(b_i\) 的过程中，用状态数组 \(f_i\) 记录 \(a_i\) 是否为尚未遍历的 \(b\) 数组元素，再计算当前的 \(b_i\) 有多少可能得答案即可。若没有，则无解，输出零

D.Sum

洛谷链接& CF 链接

哎哎原来还是结论题吗

考虑“每个数组单调不降”这个条件有什么用，差分没前途，那只能在不等关系上做文章了。现考虑两个单调不降的数组，我们取了若干个数如下图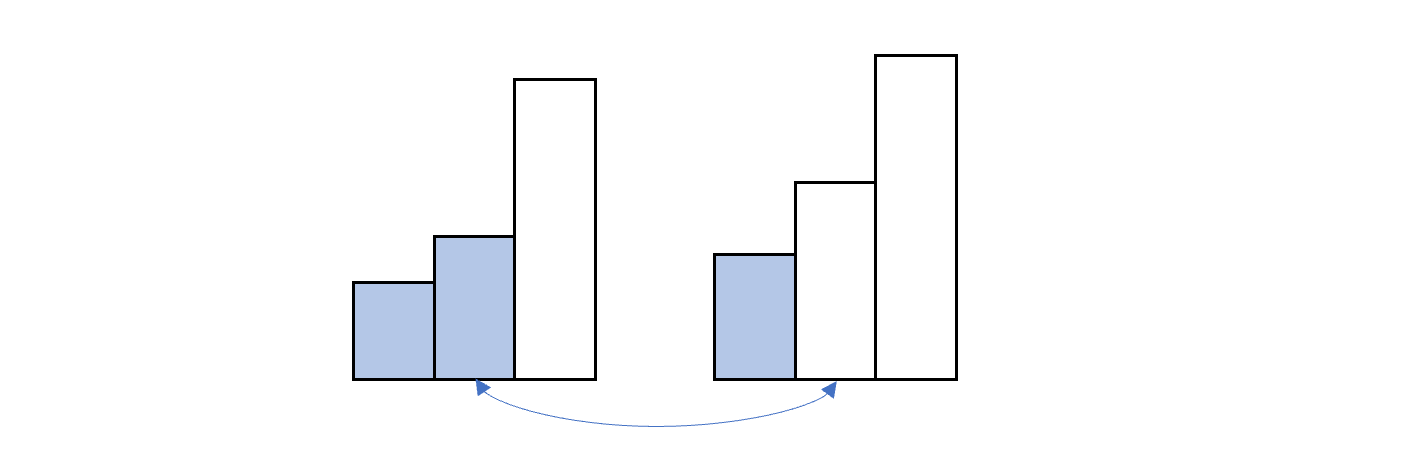

比较已选前缀最后的元素与另一前缀之后的元素，若前者小于后者，那么将第一个前缀所占用的体积全部给第二组肯定不会使得结果更劣，此时最多有一个数组没有选全部元素；推广至多个数组，仍是最多一个数组没有全部选完

那么我们可以枚举这个没全选完的数组 \(i\)，将其他的每个数组看成一个物品后背包 DP。此时相当于要在完整的背包 DP 中撤销每一个物品的贡献，考虑分治。（感觉神似线段树分治啊）设当前的分治区间为 \([l,r],m=\frac{l+r}{2}\)，因为所有物品都会在不包含它的区间中插入，所以当递归 \([l,m]\) 区间时，DP 数组中插入了 \([m+1,r]\) 的所有物品；反之递归 \([m+1,r]\) 时，DP 数组撤销并插入 \([l,m]\) 的物品。这样就完成了 DP 的撤销，复杂度 \(O(nk\log n)\)

E.Black, White and Grey Tree

洛谷链接& CF 链接

性质题。

考虑没有灰点的情况。将树上同色的联通块压缩成一个节点，此时树上每条边都连接着不同颜色的节点。最优的方案即为 每次删除同种颜色的所有叶子，这样操作可以使得树始终连通且每次删除的节点尽可能多，这个操作次数即为 \(\lfloor\frac{直径长度}{2}\rfloor+1\)。

有灰点存在时，我们需要将灰点染色并使得树缩点后的直径尽可能短。对于叶子 \(u\)，若删掉该节点后其灰色父节点会成为新的叶子节点，那么将父节点染色为和该节点相同的颜色一起删除即可。复杂度 \(O(n)\)