DataWhale八月组队学习-李宏毅深度学习Task03-误差来源与梯度下降
误差的来源
- 第一个误差来源是
bias - 第二个误差来源是
variance
1 估测
-
估测
Bias和Variance-
想要去估测
x的平均值-
假设估计量
-
从
x中设立有限个数的样本点 -
得出样本点均值(注意样本点均值不等同于
x的均值,因为个数不一致)
-
多次求得
m,与x平均值进行对比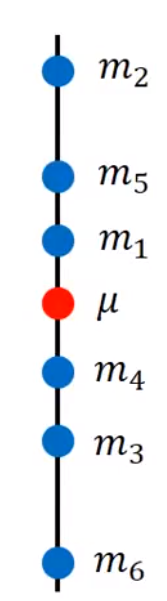
-
m的期望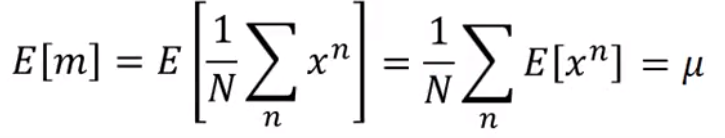
-
每一个
m和u之间的偏差量化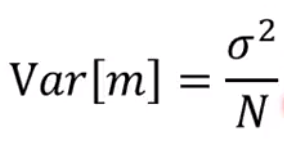
-
-
想要估测
bias-
求解
s,用来估测the variance of x
-
求其对应期望,随着
N增大,两者之前的差距就会慢慢缩小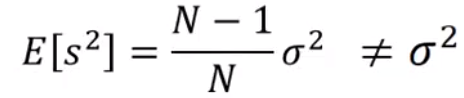
-
-
2 平行宇宙例子(指代实验次数)
在做回归的过程中,我们都会遇到bias和variance,有时候可能是bias出现偏差,有可能是variance出现偏差。训练集对应的生成的最好模型是star function,默认最优的模型是head function
-
Variance-
在所有宇宙中,我们都抓住十只宝可梦作为我们找到
star function的训练数据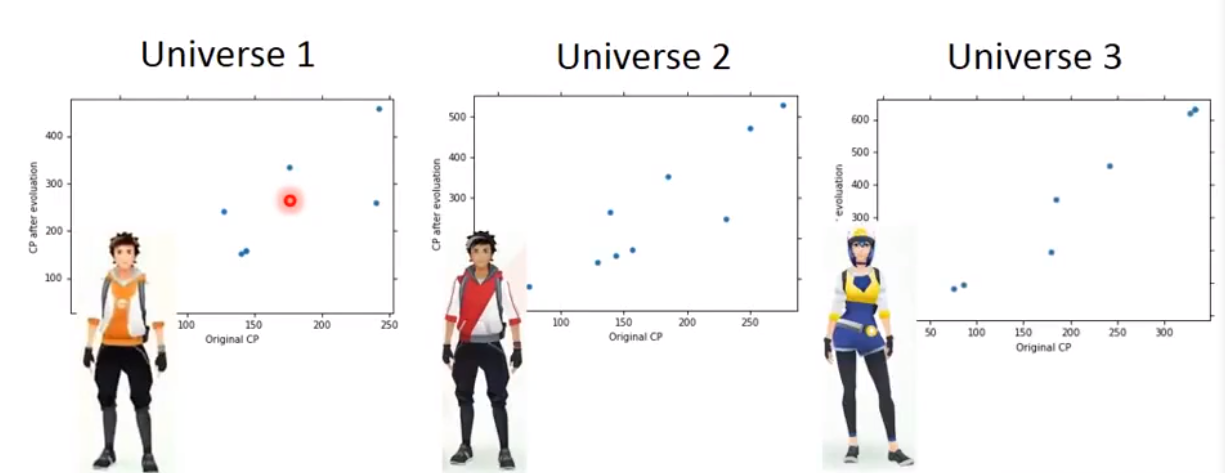
-
在不同宇宙中,全部使用相同的模型,但是得到的
star function是不同的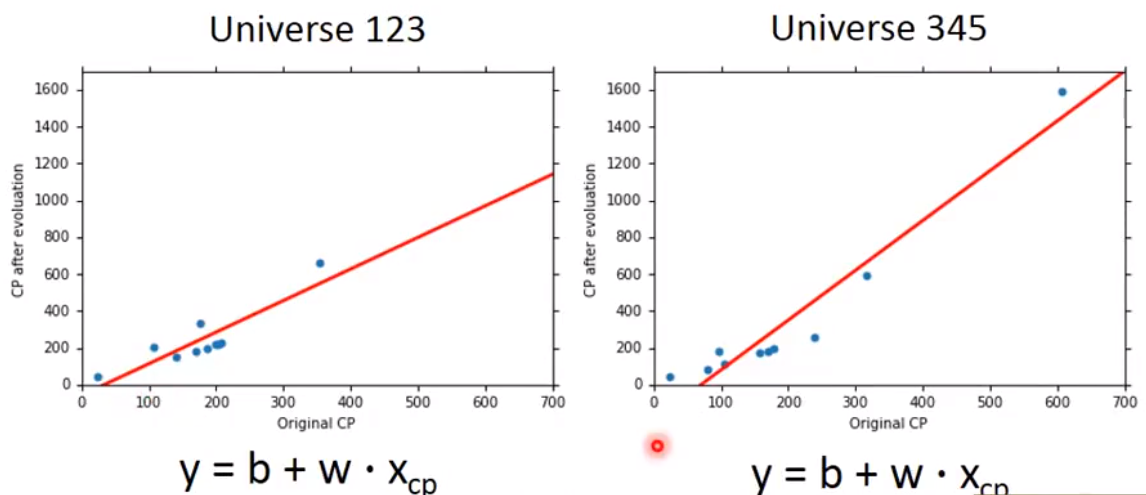
-
在100个平行宇宙中都去找寻
star function
-
更换
Model再次尝试(模型逐渐复杂)

-
发现模型越复杂,
variance越大,曲线散布很开。原因:比较简单的模型,受数据的影响会比复杂的模型更小。
-
-
Bias-
求
star function的期望值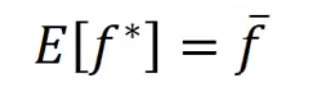
-
如果平均所有的
star function,它会更加接近head function -
发现模型越复杂,
bias越小。
-
-
Bias和Variance同时考虑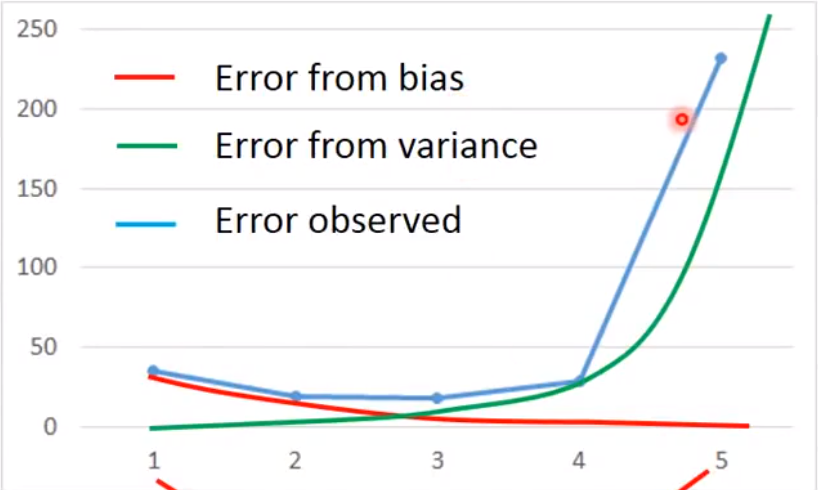
蓝线表示当同时平衡
bias和variance之后得出的error最小绿线表示误差来自于
variance很大,就是过拟合现象红线表示误差来自于
bias很大,就是欠拟合现象 -
如何判断是过拟合还是欠拟合,也就是
bias和variance哪个大?- 如果模型不能拟合训练样本,属于欠拟合现象
- 如果模型能够拟合训练样本,但在测试集上得到的一个较大的
error,属于过拟合现象。
-
针对欠拟合的改进
- 添加更多的特征作为输入
- 增加模型复杂度
-
针对过拟合的改进
- 增加样本数量
- 正则化
3 模型选择
- 模型的选择需要去平衡
bias和variance带来的影响 - 挑选能够使得误差最小的模型
- 不要根据手头已有的测试数据集(
public set)直接下定义说用哪种模型更好- 正确的做法是把测试集分为测试机和验证集,先用训练集找出最好的
star function,再用验证集来挑选模型。再把模型应用于测试数据集,得到的是实际error。
- 正确的做法是把测试集分为测试机和验证集,先用训练集找出最好的
梯度下降
1 调试学习率
- 手动设置学习率时要注意,太小太大都不好。
- 自动设置学习率
- 通常学习率随着参数的迭代更新会越来越小,
- 起始点时,离
Loss最低点距离很远,需要使用更大的学习率 - 在参数迭代数次后,学习率应当减小
- 起始点时,离
- 不同的参数应该赋予不同的学习率
- 通常学习率随着参数的迭代更新会越来越小,
2 不同的梯度下降
-
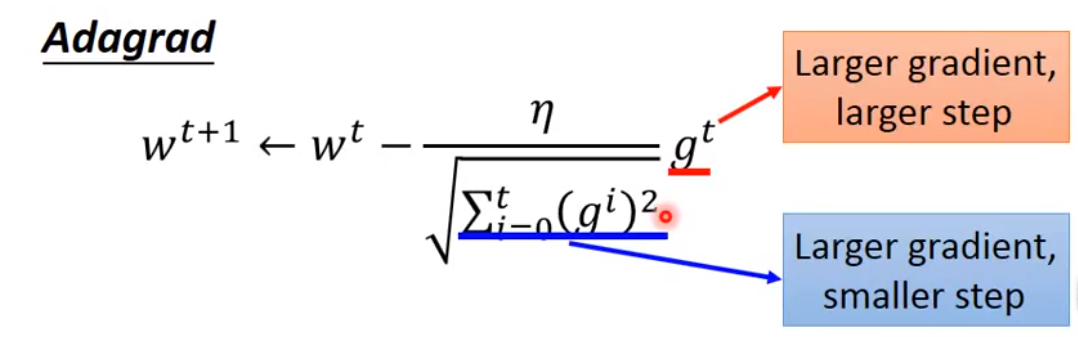
Adagrad(自适应梯度算法)-
将每个参数的学习率除以其之前导数的均方根

-
矛盾点:
-
矛盾点的解释:
- 有时候梯度会出现反差,即原先算出的梯度很小,突然算出的梯度很大。或者原先算出的梯度很大,突然算出的梯度很小。除以均方根的目的就是想了解这种造成反差的效果。
- 最好的步伐(现在的位置与最低点的距离)是同时考虑一次微分和二次微分。而二次微分可以用均方根来表示。
-
-
Stochastic Gradient Descent(随机梯度下降)-
每次只取一个样本,计算
Loss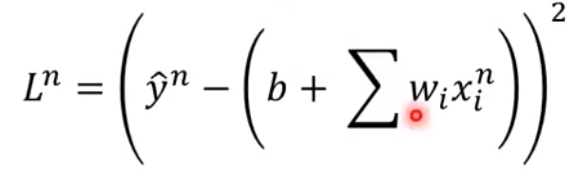
-
再更新参数(只考虑一个样本)

-
重复上述过程,所以在原先的梯度下降进行完整一次的时候,随机梯度下降已经进行了很多次梯度下降,所以速度比原先梯度下降快。
-
-
Feature Scaling(特征缩放)- 特征缩放的目的就是让每个特征的范围都限定于一个区域大小之内
- 常见做法:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号