Astar百度之星20242nd

还原汉诺塔

Problem Statement

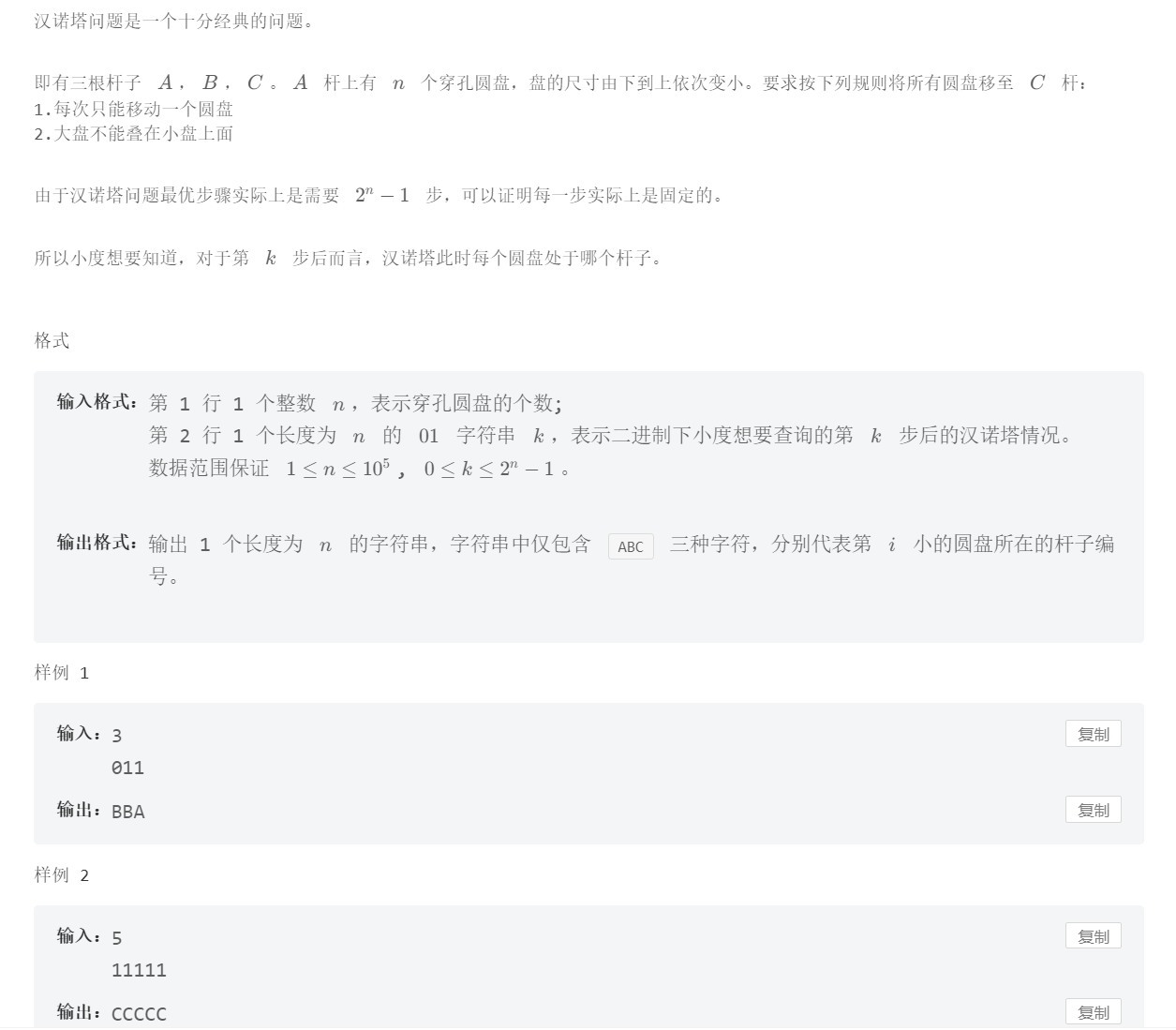
Solution

这道题确实非常巧妙，其实做的时候我就应该想到，为啥题目非要用一个二进制输入来表示第k步，这道题的汉诺塔只有三根杆子A B C，也帮我们简化了问题，我们先来模拟一下只有三个盘子的情况。

对于每一个盘子我们要将其从初始杆移到目标杆都可以将其分为三个阶段：对于从上至下第n个盘子

• 将其上层的n-1个盘子从初始杆移到过渡杆
• 将其从初始杆移到目标杆
• 将那n-1个盘子从过渡杆移到目标杆

我们可以发现这三种情况分别所需的步数

• 将其上层的n-1个盘子从初始杆移到过渡杆需\(2^{n-1}-1\)步
• 将其从初始杆移到目标杆 需1步
• 将那n-1个盘子从过渡杆移到目标杆 需\(2^{n-1}-1\)步

那么我们发现对于第n个盘子来说当进行到第\(2^{n-1}-1+1\)步时，它被移到目标杆，此后他都在目标杆，若步数小于\(2^{n-1}-1+1\)步则在初始杆。这时候我们就可以发现用二进制输入的妙处了，二进制的第n位表示\(2^{n-1}\)，也就是说当这一位为1时，当前杆子被移到了目标杆，否则没有移到。由于我们是从字符串的高位开始判断，所以为0时该杆没有被移到目标杆。

注意，每一个盘子在当前状态下的目标杆取决于它下一层的盘子想把它移到哪，所以这是层层递归的，因为对于每个杆子来说他先要被移到的杆子是不同的，我们需要不断交换A B C 杆。换句话说，我们从二进制的最高位开始遍历，如果当前位为1证明第n个盘子被移到C了，那么此时第n-1个盘子就只用完成第三步，从过渡杆移到目标杆，所以他的初始杆是上一层的过渡杆。说这么多，实际上就是每一个盘子都会影响他下层的盘子。

#include<bits/stdc++.h>
#define int long long

using namespace std;

int n;
string s;
string ans;

void solve()
{
    cin >> n >> s;

    char p0 = 'A', p1 = 'B', p2 = 'C'; //定义初始杆过渡杆目标杆分别为A B C
    
    //从最下层杆子开始分析，因为每个盘子都会影响他上层杆子的“初”“过”“目”
    for (int i = 0; i < s.size(); i ++ )
    {
        if (s[i] == '1') //当前杆子被移到了目标杆
        {
            ans += p2;
            swap(p0, p1); //下一个盘子的p0和p1被影响
        }
        else //当前杆子没有被移到目标杆
        {
            ans += p0;
            swap(p1, p2); //下一个盘子的p2和p1被影响 为了完成"第一步" 当前杆子的过渡杆是他的目标杆
        }
    }
    reverse(ans.begin(), ans.end()); //由于我们先算的是最底层第n个盘子，题目要求从小到大1~n输出盘子位于哪个杆 翻转字符串
    cout << ans << endl;
}

signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    
    solve();

    return 0;
}