Atcoder ABC 350 题解 (C - E)
Atcoder ABC 350 题解
C Sort
问题陈述
给你一个 \((1,2,\ldots,N)\) 的排列组合,\(A=(A_1,\ldots,A_N)\)
请在 \(0\) 和 \(N-1\) 之间(包括首尾两次)进行以下运算,将 \(A\) 变换为 \((1,2,\ldots,N)\) :
- 操作:选择任意一对整数 \((i,j)\) ,使得 \(1 <= i < j <= N\) .交换 \(A\) 的 \(i\) -th 和 \(j\) -th 位置上的元素。
可以证明在给定的限制条件下,总是可以把 \(A\) 变换成 \((1,2,\ldots,N)\) 。
限制因素
- \(2 \leq N \leq 2\times 10^5\)
- \(A=(A_1,\ldots,A_N)\) 是 \((1,2,\ldots,N)\) 的排列。
- 所有输入值均为整数。
输出
设 \(K\) 为操作次数。打印 \(K+1\) 行。
第一行应包含 \(K\) 。
第 \((l+1)\) 行( \(1\leq l \leq K\) )应该包含为第 \(l\) 次操作选择的整数 \(i\) 和 \(j\) ,用空格隔开。
任何满足问题陈述条件的输出都将被视为正确。
这道题需要注意的点就是输出的是原数组需要交换位置的元素的下标
题解
思路
对于当前位置i,有序数列对应的值肯定也是i,如果当前位置元素的值a[i]不等于i,那就需要将当前位置上的a[i]放到其应该放的位置(下标为a[i]的地方),我们用b[]来存每个元素当前的坐标
代码实现
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
const int N = 2e5 + 10;
int n;
int a[N], b[N]; //a数组用来存给定数组的元素 b数组用来存数组对应元素的下标
long long res;
queue<PII> q;
void solve()
{
scanf("%d", &n);
for(int i = 1; i <= n; i ++ )
{
scanf("%d", &a[i]);
b[a[i]] = i; //存当前元素在数组内的下标
}
for (int i = 1; i <= n; i ++ )
{
if (a[i] != i) //如果当前元素不与他的下标对应,将与下标对应的点换过来
{
//cout << a[i] << endl;
int pos = b[i]; //提取出来值为i的元素的下标
swap(a[i], a[pos]);
q.push({i, pos});
res ++ ;
//调换位置后,记得修改两个位置的坐标!这一步非常容易忽略!
b[a[i]] = i;
b[a[pos]] = pos;
}
}
printf("%lld\n", res);
for (int i = 0; i < res; i ++ )
{
auto t = q.front();
q.pop();
printf("%d %d\n", t.first, t.second);
}
return;
}
int main()
{
solve();
return 0;
}
代码中的关键一步
调换位置后要更新b[]存储的元素坐标
//调换位置后,记得修改两个位置的坐标!这一步非常容易忽略!
b[a[i]] = i;
b[a[pos]] = pos;
残留问题
现在还是不知道套快排板子的做法哪里出问题了 只能过\(9/14\)个数据,留到后面testcase出来之后解答
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
const int N = 2e5 + 10;
int q[N];
int res;
queue<PII> a;
void quick_sort(int q[], int l, int r)
{
if (l >= r)return;
int i = l - 1, j = r + 1, x = q[l + r >> 1];
while(i < j)
{
do i ++ ; while(q[i]<x);
do j -- ; while(q[j]>x);
if(i < j)
{
res ++ ;
a.push({i, j});
swap(q[i],q[j]);
}
}
quick_sort(q, l, j);
quick_sort(q, j + 1, r);
}
int main()
{
int n;
scanf("%d",&n);
for(int i = 0; i < n; i ++ ) scanf("%d",&q[i]);
quick_sort(q, 0, n - 1);
printf("%d\n", res);
for (int i = 0; i < res; i ++ )
{
auto t = a.front();
a.pop();
printf("%d %d\n", t.first + 1, t.second + 1);
}
return 0;
}
D New Friends
问题陈述
有一个由 \(N\) 用户使用的 SNS,标有从 \(1\) 到 \(N\) 的编号。
在这个 SNS 中,两个用户可以互为好友。
好友关系是双向的;如果用户 X 是用户 Y 的好友,则用户 Y 始终是用户 X 的好友。
目前,SNS 上有 \(M\) 对好友关系,其中 \(i\) (最多的一对)由用户 \(A_i\) 和 \(B_i\) 组成。
请确定以下操作的最大执行次数:
- 操作:选择三个用户 X、Y 和 Z,使得 X 和 Y 是好友,Y 和 Z 是好友,但 X 和 Z 不是好友。让 X 和 Z 成为好友。
Constraints
- \(2 \leq N \leq 2 \times 10^5\)
- \(0 \leq M \leq 2 \times 10^5\)
- \(1 <= A_i < B_i <= N\)
- The pairs \((A_i, B_i)\) are distinct.
- All input values are integers.
Input
The input is given from Standard Input in the following format:
\(N\) \(M\)
\(A_1\) \(B_1\)
\(\vdots\)
\(A_M\) \(B_M\)
Sample Input 1
4 3
1 2
2 3
1 4
样本输出 1
3
与朋友的朋友建立三个新朋友关系的情况如下:
- 用户 \(1\) 与其好友(用户 \(2\) )的好友用户 \(3\) 成为好友
- 用户 \(3\) 与用户 \(4\) 成为好友,而用户 \(4\) 是其好友(用户 \(1\) 的好友
- 用户 \(2\) 与其好友(用户 \(1\) )的好友用户 \(4\) 成为好友
不会有四个或更多新朋友。
题解
思路
太妙了 用并查集的知识做 刚开始还在想用搜索层层递归的思路去找
实质上朋友关系可以构成连通块,例如1 - 2 是朋友关系 1 - 4 是朋友关系,那么1 - 2 - 4 就是一个连通块
那么根据输入的朋友关系,必然会构成很多个连通块,我们的目的就是将这些相互之间独立的连通块,能连起来的都连起来成为完全连通图 ,每个完全连通图都有一个祖宗节点
则最终构成的完全连通图内有多少条边再减去输入时已经给定的边就是能新产生的边,也就是新的朋友关系数量
一个有i个点的完全连通图的边数为 \(\frac{i * (i - 1)}{2}\)
真的服了 debug半天发现还是爆int的问题 一直在那想我的思路为啥不对
长记性了 以后做啥题都必须加#define int long long!(记得不能加分号;哦)
题目给的点最多\(2*10^5\)个,那么由这些点构成的边就最多有 \(\frac{2* 10^5 * (2 * 10^5 - 1)}{2}\) 这么多条 超过2e9了,肯定会爆int!
代码实现
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
#define int long long
int n, m;
int p[N], cnt[N], sz[N]; //p[]存每个点的祖宗节点 cnt[]记录当前连通块内已经存在的边的数量 sz[]记录当前连通块内点的数量
long long res;
//找连通块内的祖宗节点
int find(int x)
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
void solve()
{
scanf("%lld%lld", &n, &m);
//初始化每个连通块由每个点自身构成 祖宗节点是他自己 连通块内点的数量为1
for (int i = 1; i <= n; i ++ )
{
p[i] = i;
sz[i] = 1;
}
while (m -- )
{
int a, b;
scanf("%lld%lld", &a, &b);
int u = find(a), v = find(b);
if (u == v) //找a和b的祖宗节点, 如果a和b位于同一连通块内
{
cnt[u] ++ ; //该连通块内已经存在的边的数量++(利用祖宗节点作为标志记录)
}
else //若不在同一连通块 将这两个连通块合并
{
p[u] = v; //把a所在连通块接到b所在连通块里面
sz[v] += sz[u]; //a所在连通块点的数量加到b所在连通块点的数量
cnt[v] += cnt[u] + 1; //a所在连通块点已存在的边数加到b连通块已存在的边数 记得加上本次读取到的给定边a到b
}
}
for (int i = 1; i <= n; i ++ ) //遍历所有点找各个连通块的祖宗节点
{
if (find(i) == i) //如果点i就是他所在连通块的祖宗节点 开始操作
{
res += (sz[i] * (sz[i] - 1)) / 2 - cnt[i]; //构成当前完全连通图所需操作数就是图内总边数减去已存在的边数
}
}
printf("%lld\n", res);
return;
}
signed main()
{
solve();
return 0;
}
一个不良的习惯
刚开始是这么写的
else
{
sz[find(b)] += sz[find(a)];
cnt[find(b)] += cnt[find(a)] + 1;
p[find(a)] = find(b); 这行代码必须写在最后 要不然会提前将find(b)改变
}
如果我先写了p[find(a)] = find(b);那操作就出错了,提前将find(b)改变了,导致另外两行代码就没法执行了,一个隐形的错误在比赛的时候是很难发现的,我们要学会创建临时变量,临时变量是不会更改的,注意这个细节
E Toward 0
问题陈述
给你一个整数 \(N\) 。你可以进行以下两种运算:
- 支付 \(X\) 日元,将 \(N\) 替换为 \(\displaystyle\left\lfloor\frac{N}{A}\right\rfloor\) 。
- 支付 \(Y\) 日元,掷出一个骰子(骰子),该骰子以相等的概率显示 \(1\) 和 \(6\) 之间的整数。让 \(b\) 成为掷骰子的结果,用 \(\displaystyle\left\lfloor\frac{N}{b}\right\rfloor\) 代替 \(N\) 。
这里, \(\lfloor s \rfloor\) 表示小于或等于 \(s\) 的最大整数。例如, \(\lfloor 3 \rfloor=3\) 和 \(\lfloor 2.5 \rfloor=2\) 。
求在最优化选择操作时, \(N\) 变为 \(0\) 之前支付的最小预期成本。
每次操作的掷骰子结果与其他掷骰子结果无关,可以在观察前面操作的结果后选择操作。
Constraints
- \(1 \leq N \leq 10^{18}\)
- \(2 \leq A \leq 6\)
- \(1 \leq X, Y \leq 10^9\)
- All input values are integers.
题意解释
每次选择给X或Y元,求将N变为0的最小成本
也就是求能够使N变成0最小的期望代价
题解
思路
期望DP的简单应用(第一次遇到 )
简单的期望DP普遍利用移项法做(本题做法),难的用高斯消元
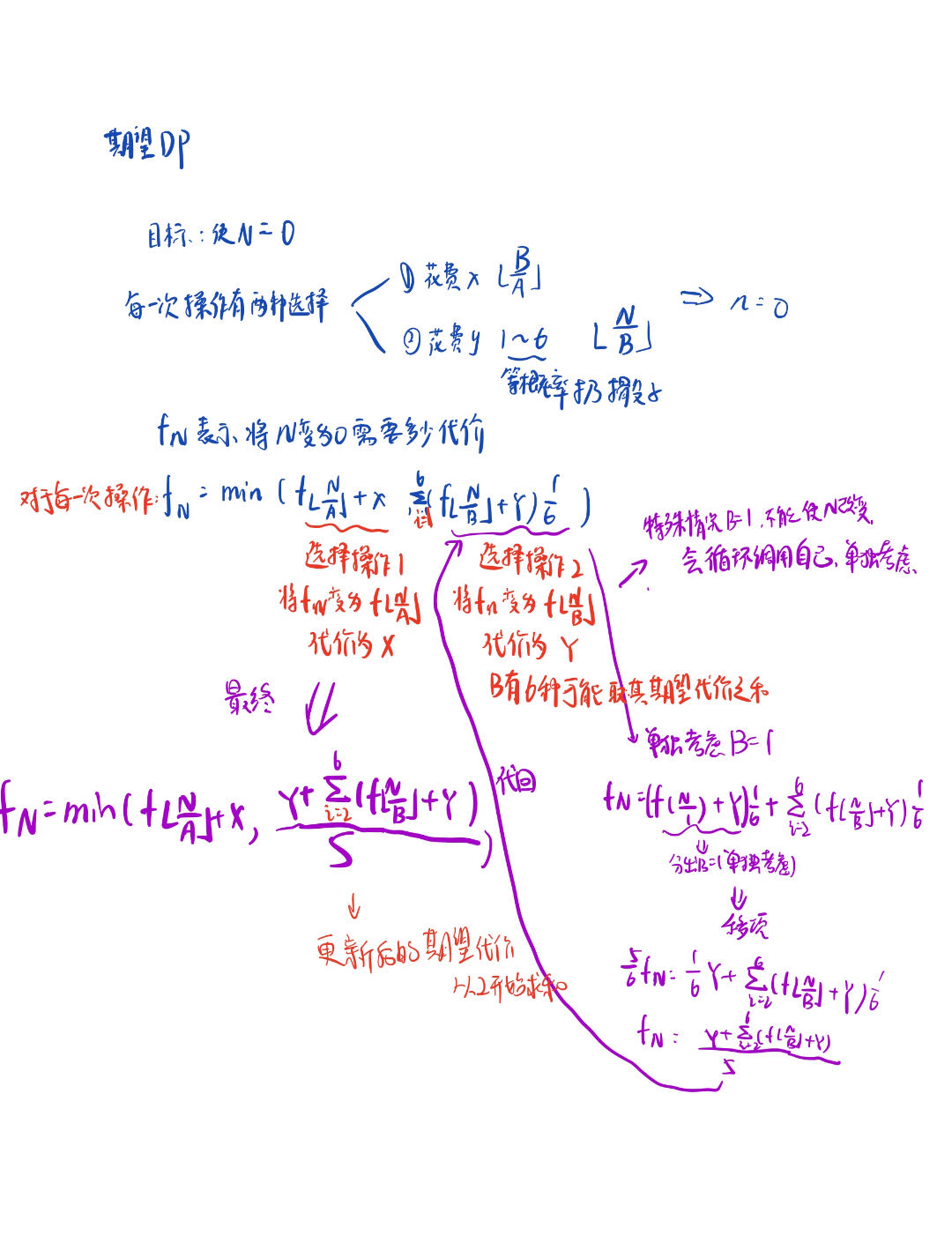
代码实现 (利用记忆化搜索)
#include <bits/stdc++.h>
using namespace std;
#define int long long
int n, a, x, y;
map <int, double> f; //存一下每次对N操作后的整数和其对应所需花费最小代价
double dp(int m) //注意这里要定义成double!
{
if (!m) return 0; //如果N本来就是0 直接退出函数
if (f[m]) return f[m]; //如果当前对应整数已经算出他需要花费的最小代价 返回当前操作所需代价
double sum = y; //初始化为y 看写出来的状态表达式分子多了一个y 在这里加上
for (int i = 2; i <= 6; i ++ ) //从扔到点数2开始算操作②的平均期望代价
{
sum += dp(m / i) + y; //扔到当前点数i的代价就是 当前操作使得数变为m / i后去继续找dp(m / i)的最小代价 + 当前操作代价y
//注意求sum这里会层层递归 最后层层返回 这就是记忆化搜索的妙处
}
sum /= 5; //根据状态表达式 求出操作②的平均期望代价
f[m] = min(sum, dp(m / a) + x); //将当前数运算到0的最小代价就是 操作①的代价 和 操作②的代价 求min
return f[m];
}
void solve()
{
cin >> n >> a >> x >> y;
cout << fixed << setprecision(8) << dp(n) << endl; //题目要求误差低于1e-6
return;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0);
solve();
return 0;
}
对样例2的模拟
Sample Input 2
3 2 20 20
Sample Output 2
32.000000000000000



 浙公网安备 33010602011771号
浙公网安备 33010602011771号