Day3 数据结构
Vector
定义方式:vector
有时压入数字时会自动开原空间的两到三倍。
末尾压入容器:a.push_back(x);
在末尾弹出容器:a.pop_back();
清空容器:a.clear();
查询元素个数:a.size();
首指针:a.begin();
插入元素在sit位置:a.insert(sit,x);其中sit是vector的迭代器。
Stack-先进后出
在末尾压入容器:a.push_back(x);
在末尾弹出容器:a.pop_back();
清空容器:a.clear();
查询元素个数:a.size();
首指针:a.begin();
插入元素在sit位置:a.insert(sit,x);其中sit是vector的迭代器。
其它像数组一样调用就可以了。
看做是一个动态数组
若没有元素时top会返回NULL
用两个栈表示一个队列的效果
把数压入a栈,然后依次弹出压入b栈,从b栈开始取。可达到队列效果。a为临时栈。
Queue
定义:queue
插入队尾:a.push(x);
删除队首:a.pop();
查询队尾:a.back();
查询队首:a.front();
查询长度:a.size();
清空只能慢慢pop。
搜索树
它可以用作字典,也可以用作优先队列。
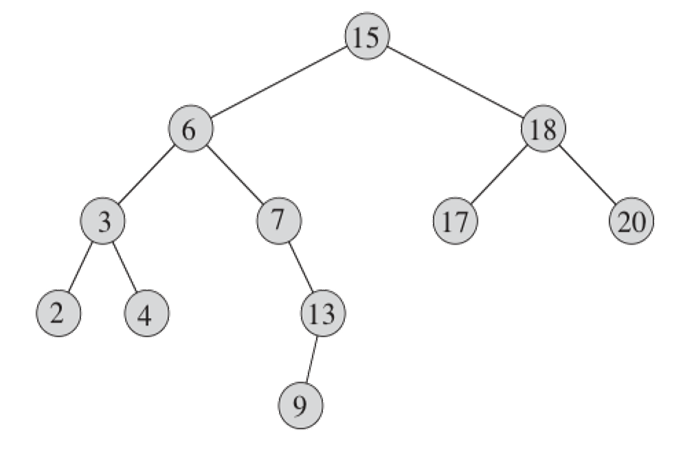
如图所示,一颗二叉查找树是按二叉树结构来组织的。
这样的树可以用链表结构表示,其中每一个节点都是一个对象。
节点中包含 key, left, right 和 parent。
如果某个儿子节点或父节点不存在,则相应域中的值即为 NULL。
设 x 为二叉查找树中的一个节点。
如果 y 是 x 的左子树的一个节点,则 key[y] <= key[x].
如果 y 是 x 的右子树的一个节点,则 key[x] <= key[y].
二叉查找树的中序遍历
inorder(int x)
{
if x != NULL{
inorder(left[x]);
printf(%d,key[x]);
inorder(right[x]);
}
}
若随机的数构造时一般使用二叉搜索树
如果各元素按照随机的顺序插入,则构造出的二叉查找树的期望高度为 O(log n)。
二叉查找树的查询
与二叉查找树的遍历相同原理,代码:
tree_search(int x,int k)
{
if(x==NULL||k==key[x])
return x;
if(k<key[x])
return tree_search(left[x],k);
else
return tree_search(right[x],k);
}
二叉查找树查找最小/最大元素
最小元素
tree-Minimum(x)
{
while(left[x]!=NULL)
x=left[x];
return x;
}
最大元素
tree-Minimum(int x)
{
while(right[x]!=NULL)
x=right[x];
return x;
}
二叉查找树的前驱和后继
tree-successor(int x)
{
if(right[x]!=NULL)
return tree-Minimum(right[x])
y=parent[x];
while(y!=NUll&&x==right[y])
{
x=y;
y=parent[y];
}
return y;
}
while(y!=NUll&&x==right[y])
{
x=y;
y=parent[y];
}
此段代码:若当前要求后继的点没有右子节点,需要找到当他不作为右子节点的父节点的值即为所求。
如图:
二叉查找树的插入
Tree-Insert(int t,int z)
{
int y=NULL,x=root[t];
while(x!=NULL)
{
y=x;
if(key[z]<key[x])
x=left[x];
else
x=right[x];
}
parent[z]=y;
if(y==NULL)
root[t]=z;
else if(key[z]<key[y])
left[y]=z;
else right[y]=z;
}
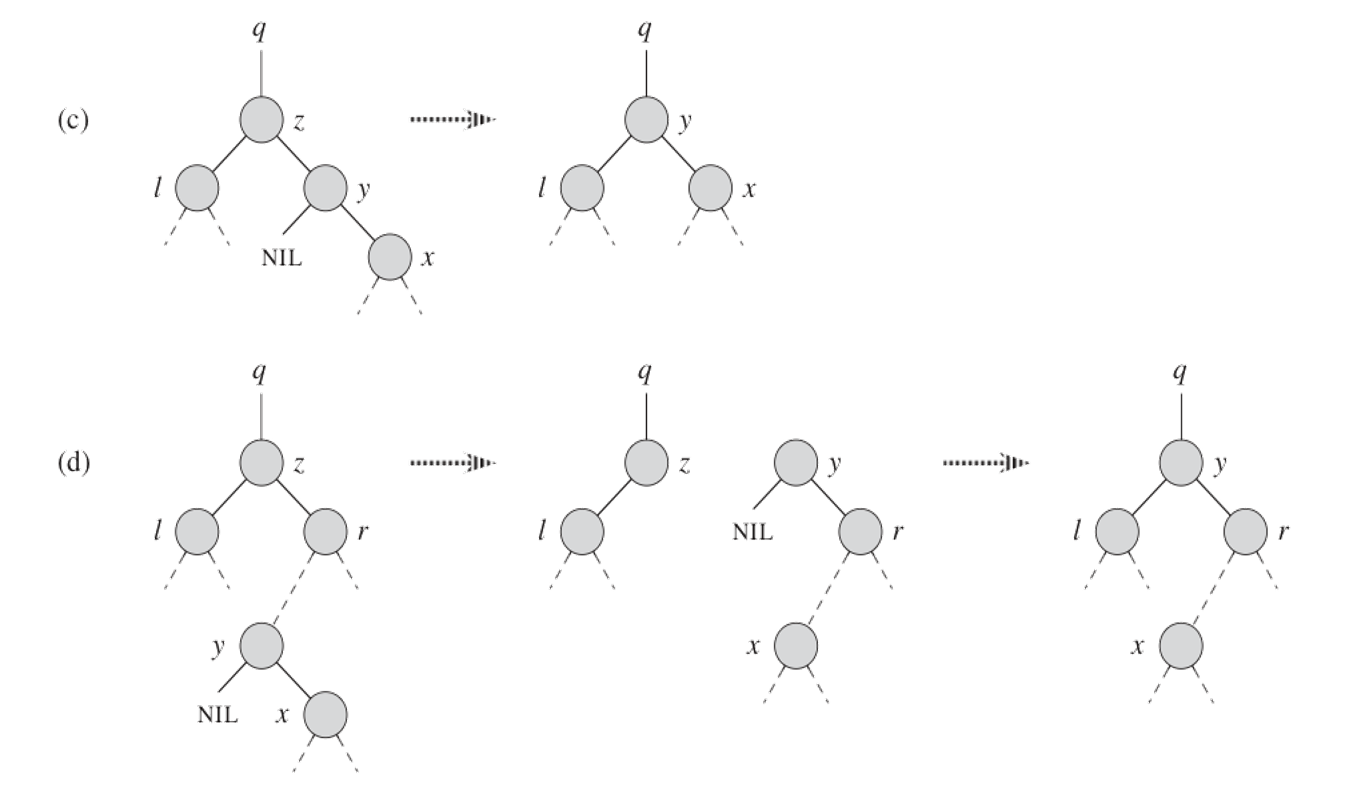
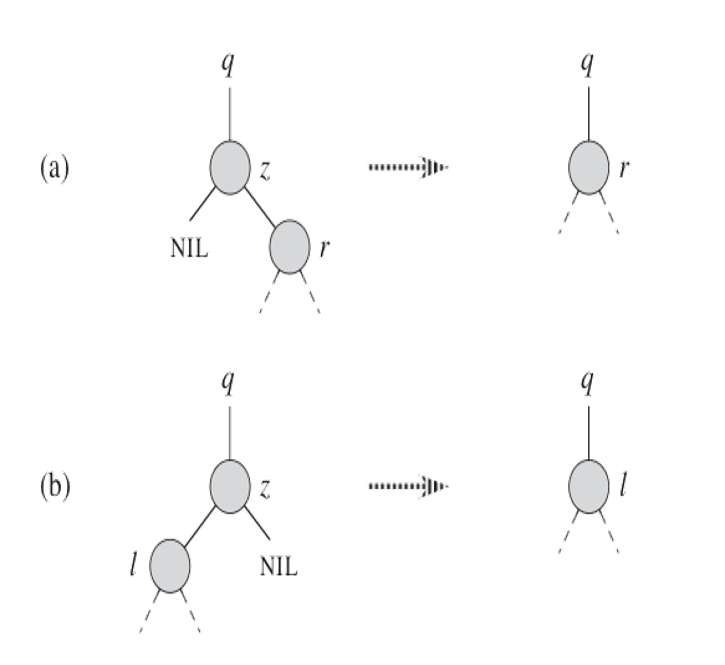
二叉查找树的删除
四种情况
堆(Heap)
堆的性质
- 完全二叉树的层次序列,可以用数组表示。
- 堆中储存的数是局部有序的,堆不唯一。
- 节点的值与其孩子的值之间存在限制。
- 任何一个节点与其兄弟之间都没有直接的限制。
- 从逻辑角度看,堆实际上是一种树形结构。
最小根堆和二叉查找树的区别
对于二叉搜索树的任意一个节点:
- 左子树的值都小于这个节点的值
- 右子树的值都大于这个节点的值
- 两个子树都是二叉搜索树
- 对于最小堆的任意一个节点:
- 所有的子节点值都大于这个节点的值
- 两个子树都是最小堆
eg1
给出两个长度为 n 的有序表 A 和 B,在 A 和 B 中各任取一个元素,可以得到 n2 个和,求这些和中最小的 n 个。
n <= 400000
分析:一共有n^2个和:
A[1] + B[1], A[1] + B[2], …, A[1] + B[n]
A[2] + B[1], A[2] + B[2], …, A[2] + B[n]
…
A[n] + B[1], A[n] + B[2], …, A[n] + B[n]
固定 A[i], 每 n 个和都是有序的:
A[1] + B[1] <= A[1] + B[2] <= … <= A[1] + B[n]
A[2] + B[1] <= A[2] + B[2] <= … <= A[2] + B[n]
…
A[n] + B[1] <= A[n] + B[2] <= … <= A[n] + B[n]
a[1]b[1]是最小的,第二小的可能是a[1]b[2],a[2]b[1]。就每次把这一个点右边和下边的数字压进去,找到最小的然后弹出。
每一次找一列 每一次找挑出最大的 一定是第几次的最小和:所以先把第一列放入根堆,找到最小然后弹出后,找到这一个点右边的点压入根堆,继续进行比较,重复上述过程。
暴力代码
int main()
{
int n=read();
for(int i=1;i<=n;++i) a[i]=read();
for(int i=1;i<=n;++i) b[i]=read();
for(int i=1;i<=n;++i)
{
for(int j=1;j<=n;++j)
{
int x=a[j]+b[i];
q.push(x);
}
int x=q.top();
q.pop();
cout<<x<<" ";
}
return 0;
}
优化版代码:
用结构体给,需要重载运算符。
最好可以用pair。
int main()
{
int n=read();
for(int i=1;i<=n;++i) a[i]=read();
for(int i=1;i<=n;++i) b[i]=read();
for(int i=1;i<=n;++i)
{
if(!q.empty())
{
Node v=q.top();
u.sum=a[v.y+1]+b[v.x];
u.x=v.y+1;u.x=j;
}
u.sum=a[j]+b[i];
u.x=i;u.y=j;
q.push(u);
}
return 0;
}
bool operator < (const node& a, const node&b) {
return a.x<b.x;
}
eg2
丑数是指质因子在集合 {2, 3, 5, 7} 内的整数,第一个丑数是 1.现在输入 n,输出第 n 大的丑数。
n <= 10000.
#include<iostream>
#include<cstdio>
#include<queue>
#include<vector>
#include<cmath>
#include<stack>
using namespace std;
int n,cnt=0;
priority_queue<<int> vector<int>, greater<int> > q;
inline int read()
{
int s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){s=s*19+ch-'0';ch=getchar();}
return s*w;
}
inline void ugly(int n,int a,int b,int c,int d,int x,int cnt)
{
if(cnt==n) return;
q.push(pow(2,a+1)*pow(3,b)*pow(5,c)*pow(7,d))
if(pow(2,a+1)*pow(3,b)*pow(5,c)*pow(7,d)==x) q.pop();
return ugly(a+1,b,c,d,pow(2,a+1)*pow(3,b)*pow(5,c)*pow(7,d),cnt+1);
q.push(pow(2,a)*pow(3,b+1)*pow(5,c)*pow(7,d))
if(pow(2,a)*pow(3,b+1)*pow(5,c)*pow(7,d)==x) q.pop();
return ugly(a,b+1,c,d,pow(2,a)*pow(3,b+1)*pow(5,c)*pow(7,d),cnt+1);
q.push(pow(2,a)*pow(3,b)*pow(5,c+1)*pow(7,d))
if(pow(2,a)*pow(3,b)*pow(5,c+1)*pow(7,d)==x) q.pop();
return ugly(a,b,c+1,d,pow(2,a)*pow(3,b)*pow(5,c+1)*pow(7,d),cnt+1);
q.push(pow(2,a)*pow(3,b)*pow(5,c)*pow(7,d+1))
if(pow(2,a)*pow(3,b)*pow(5,c)*pow(7,d+1)==x) q.pop();
return ugly(a,b,c,d+1,pow(2,a)*pow(3,b)*pow(5,c)*pow(7,d+1),cnt+1);
}
int main()
{
int a,b,c,d,x;
n=read();
a=b=c=d=0;
x=pow(2,a)*pow(3,b)*pow(5,c)*pow(7,d);
q.push(x);
ugly(a,b,c,d,x);
for(int i=1;i<=n;++i)
{
int y=q.top();q.pop();
if(i==n)
cout<<y<<endl;
}
return 0;
}
线段树
线段树1:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define ull unsigned long long
const int Maxn=100001;
ull n,m,a[Maxn],ans[Maxn<<2],tag[Maxn<<2];
inline ull read()
{
int s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){s=s*10+ch-'0';ch=getchar();}
return s*w;
}
inline ull ls(ull x)
{
return x<<1;
}
inline ull rs(ull x)
{
return x<<1|1;
}
void scan()
{
n=read();m=read();
for(int i=1;i<=n;++i)
a[i]=read();
}
inline void pushup(ull p)
{
ans[p]=ans[ls(p)]+ans[rs(p)];
}
void build(ull p,ull l,ull r)
{
tag[p]=0;
if(l==r){ans[p]=a[l];return;}
ull mid=(l+r)>>1;
build(ls(p),l,mid);
build(rs(p),mid+1,r);
pushup(p);
}
inline void f(ull p,ull l,ull r,ull k)
{
tag[p]=tag[p]+k;
ans[p]=ans[p]+k*(r-l+1);
}
inline void pushdown(ull p,ull l,ull r)
{
ull mid=(l+r)>>1;
f(ls(p),l,mid,tag[p]);
f(rs(p),mid+1,r,tag[p]);
tag[p]=0;
}
inline void update(ull nl,ull nr,ull l,ull r,ull p,ull k)
{
if(nl<=l&&r<=nr)
{
ans[p]+=k*(r-l+1);
tag[p]+=k;
return;
}
pushdown(p,l,r);
ull mid=(l+r)>>1;
if(nl<=mid) update(nl,nr,l,mid,ls(p),k);
if(nr>mid) update(nl,nr,mid+1,r,rs(p),k);
pushup(p);
}
ull query(ull qx,ull qy,ull l,ull r,ull p)
{
ull res=0;
if(qx<=l&&r<=qy) return ans[p];
ull mid=(l+r)>>1;
pushdown(p,l,r);
if(qx<=mid) res+=query(qx,qy,l,mid,ls(p));
if(qy>mid) res+=query(qx,qy,mid+1,r,rs(p));
return res;
}
int main()
{
ull a1,b,c,d,e,f;
scan();
build(1,1,n);
while(m--)
{
a1=read();
switch(a1)
{
case 1:{
b=read();c=read();d=read();
update(b,c,1,n,1,d);
break;
}
case 2:{
e=read();f=read();
printf("%lld\n",query(e,f,1,n,1));
break;
}
}
}
return 0;
}
线段树2:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef unsigned long long ull;
const int Maxn=200002;
ull n,m,MOD,a[Maxn];
struct Node{
ull sum,multag,addtag;
}tr[Maxn<<2];
inline ull read()
{
ull w=1,s=0;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){s=s*10+ch-'0';ch=getchar();}
return s*w;
}
inline ull ls(ull x){return x<<1;}
inline ull rs(ull x){return x<<1|1;}
inline void pushup(ull p)
{
tr[p].sum=(tr[ls(p)].sum+tr[rs(p)].sum)%MOD;
return;
}
inline void scan()
{
n=read();m=read();MOD=read();
for(register ull i=1;i<=n;++i)
a[i]=read();
return;
}
inline void build(ull l,ull r,ull p)
{
tr[p].multag=1;
tr[p].addtag=0;
if(l==r){tr[p].sum=a[l];return;}
ull mid=(l+r)>>1;
build(l,mid,ls(p));
build(mid+1,r,rs(p));
pushup(p);
return;
}
inline void pushdown(ull l,ull r,ull p)
{
ull mid=(l+r)>>1;
tr[ls(p)].sum=(tr[ls(p)].sum*tr[p].multag%MOD+tr[p].addtag*(mid-l+1)%MOD)%MOD;
tr[rs(p)].sum=(tr[rs(p)].sum*tr[p].multag%MOD+tr[p].addtag*(r-mid)%MOD)%MOD;
tr[ls(p)].addtag=(tr[ls(p)].addtag*tr[p].multag%MOD+tr[p].addtag)%MOD;
tr[rs(p)].addtag=(tr[rs(p)].addtag*tr[p].multag%MOD+tr[p].addtag)%MOD;
tr[ls(p)].multag=(tr[p].multag*tr[ls(p)].multag)%MOD;
tr[rs(p)].multag=(tr[p].multag*tr[rs(p)].multag)%MOD;
tr[p].multag=1;
tr[p].addtag=0;
return;
}
inline void upd1(ull nl,ull nr,ull l,ull r,ull p,ull k)
{
if(nl<=l&&r<=nr)
{
tr[p].addtag=(tr[p].addtag+k)%MOD;
tr[p].sum=(tr[p].sum+k*(r-l+1)%MOD)%MOD;
return;
}
pushdown(l,r,p);
ull mid=(l+r)>>1;
if(nl<=mid) upd1(nl,nr,l,mid,ls(p),k);
if(nr>mid) upd1(nl,nr,mid+1,r,rs(p),k);
pushup(p);
return;
}
inline void upd2(ull nl,ull nr,ull l,ull r,ull p,ull k)
{
if(nl<=l&&r<=nr)
{
tr[p].addtag=tr[p].addtag*k%MOD;
tr[p].multag=tr[p].multag*k%MOD;
tr[p].sum=tr[p].sum*k%MOD;
return;
}
ull mid=(l+r)>>1;
pushdown(l,r,p);
if(nl<=mid) upd2(nl,nr,l,mid,ls(p),k);
if(nr>mid) upd2(nl,nr,mid+1,r,rs(p),k);
pushup(p);
return;
}
inline ull query(ull ql,ull qr,ull l,ull r,ull p)
{
ull res=0;
if(ql<=l&&r<=qr){return tr[p].sum;}
ull mid=(l+r)>>1;
pushdown(l,r,p);
if(ql<=mid) res+=query(ql,qr,l,mid,ls(p));
if(qr>mid) res+=query(ql,qr,mid+1,r,rs(p));
return res%MOD;
}
inline void print(int l,int r,int p)
{
if(l==r) {printf("%lld ",tr[p].sum);return;}
int mid=(l+r)>>1;
print(l,mid,ls(p));
print(mid+1,r,rs(p));
return;
}
int main()
{
scan();
build(1,n,1);
while(m--)
{
ull o,x,y,z;
o=read();
switch(o)
{
case 1:{
x=read();y=read();z=read();
upd2(x,y,1,n,1,z);
break;
}
case 2:{
x=read();y=read();z=read();
upd1(x,y,1,n,1,z);
break;
}
case 3:{
x=read();y=read();
printf("%lld\n",query(x,y,1,n,1));
break;
}
}
}
return 0;
}
问题1:有一个长度为 n 的序列,a[1], a[2], …, a[n]。现在执行 m 次操作,每次可以执行以下两种操作之一:
1. 将下标在区间 [l, r] 的数都加上 v。
2. 询问一个下标区间 [l, r] 中所有数的最小值的个数。
修改部分:在pushup里注意两点:
1.如果两个子点的最小值相等,父节点的最小值个数就是两个儿子最小值个数相加。
2.如果两个子点的最小值不相等,比较两者最小值,更新父节点的最小值。
if(Min[ls(x)]==Min[rs(x)])
{
cnt[x]=cnt[ls(x)]+cnt[rs(x)];
Min[x]=Min[ls(x)];
}
else
{
if(Min[ls(x)]>Min[rs(x)])
{
Min[x]=Min[rs(x)];
cnt[x]=cnt[rs(x)];
}
else
{
Min[x]=Min[ls(x)];
cnt[x]=cnt[ls(x)];
}
}
问题2:你有一个长度为 n 的序列 A[1], A[2], …, A[N].
询问:Query(x, y) = max { A[i] + … + A[j]; x <= i <= j <= y}给出 M 组 (x, y),请给出 M 次询问的答案。
|A[i]| <= 15007, 1 <= N,M <= 50000
出处:SPOJ GSS1 Can you answer these queries I
分析:考虑用线段树来维护每个区间的答案。需要考虑如何传递合并子节点的结果:
关键引入:后缀和与前缀和一同使用
设x结点的答案为smax[x],区间前缀和最大值为lmax[x],后缀最大和rmax[x];
此时有两种情况:
-
所求区间x到y完整覆盖了x点的区间:smax[x]=max(smax[ls],smax[rs]);
-
所求区间x到y未完全覆盖x点的区间:smax[x]=rmax[ls]+lmax[rs];
故最终smax[x]=max(max(smax[ls],smax[rs]),rmax[ls]+lmax[rs]);
怎样更新 lmax和rmax?
1.lmax[x]=max(lmax[ls],sum[ls]+lmax[rs]);
2.rmax[x]=max(rmax[rs],sum[rs]+rmax[ls]);
建树时上述的值都相等 故有:
if (l == r){
smax[x] = lmax[x] = rmax[x] = sum[x] = a[l];
return;
}
你有一个长度为 n 的序列 A[1], A[2], …, A[N].
询问:
Query(x1, y1, x2, y2) = max { A[i] + … + A[j]; x1 <= i <= y1, x2 <= j <= y2}
x1 <= x2, y1 <= y2
给出 M 组操作,输出每次询问的答案
|A[i]| <= 10000, 1 <= N,M <= 10000
出处:SPOJ GSS5 Can you answer these queries V
分析:解题关键——是否存在交集。
如果 [x1, y1] 和 [x2, y2] 没有交集,即 y1 < x2
答案显然等于: Rmax([x1, y1]) + Sum(y1 + 1, x2 - 1) + Lmax([x2, y2])
如果 [x1, y1] 和 [x2, y2] 有交集,即 y1 >= x2
这个时候,区间分为三个部分:
[x1, x2 - 1], [x2, y1], [y1 + 1 .. y2]
左端点有两种选择,右端点也有两种选择,一共四种情况。
进一步讨论,变为三种情况:
Smax([x2, y1])
Rmax([x1, x2 - 1]) + Lmax([x2, y2])
Rmax([x1, y1]) + Lmax([y1 + 1 .. y2])
DFS序
可以将一维形式转化为二维形式。通过遍历一个点的进出顺序写成区间的形式。
一定可以构造一个线段树。
LCA
定义:给出有根树T中的两个不同的节点u和v,找到一个离根最远的节点x,使得x同时是u和v的祖先,x就是u和v的最近公共祖先(Lowest common ancestor)
例子:
B和M的最近公共祖先是A
K和J的最近公共祖先是D
C和H的最近公共祖先是C
注:可以把自己当作祖先
倍增算法
我们记fa[u]为u的父节点,即从u向根走1步能到达的节点,对根节点我们记fa[root] = 0.
记up [u] [k] 为从u向根走2k步到达的节点。
显然有
up [u] [0] = fa[u]
up [u] [k] = up [ up [u] [k – 1] ] [k – 1] 递推关系式
例如
up [“K”] [0] = “I”,
up [”I”] [0] = ”D”,
up [”K”] [1] = “D”.
深度:到根据节点的距离,可以自定标准。
具体实现
第一步:把节点的深度化为相同,让深度更深的节点用倍增算法向上走;特殊情况:若一个点是另一个点的祖先,将会重合于同一祖先点,则可以停止寻找。
第二步(深度相同且不在同一节点):让u和v同时向上跳跃,每次跳
注:祖先的祖先还是祖先,故不可以从大到小枚举。
###### 任何十进制数都可以转换成2的n次幂的和
复杂度:O(log(n))
代码实现
#include<bits/stdc++.h>
using namespace std;
const int MAXN=500001;
struct node{
int nxt,to;
}e[MAXN<<1];
int h[MAXN];
int n,m,s,cnt;
void add(int x,int y)
{
++cnt;
e[cnt].to=y;
e[cnt].nxt=h[x];
h[x]=cnt;
}
int D[MAXN],f[MAXN][21];
void dfs(int r,int fa)
{
D[r]=D[fa]+1;
f[r][0]=fa;
for(int i=1;(1<<i)<=D[r];i++)
f[r][i]=f[f[r][i-1]][i-1];
for(int i=h[r];i;i=e[i].nxt)
{
int v=e[i].to;
if(v!=fa) dfs(v,r);
}
}
int lca(int x,int y)
{
if(D[x]<D[y]) swap(x,y);
for(int i=20;i>=0;i--)
{
if(D[y]<=D[x]-(1<<i))
x=f[x][i];
}
if(x==y) return y;
for(int i=20;i>=0;i--)
{
if(f[x][i]!=f[y][i])
{
x=f[x][i];
y=f[y][i];
}
}
return f[x][0];
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin>>n>>m>>s;
for(int i=1;i<n;i++)
{
int x,y;
cin>>x>>y;
add(x,y);
add(y,x);
}
dfs(s,0);
for(int i=1;i<=m;i++)
{
int a,b;
cin>>a>>b;
cout<<lca(a,b)<<endl;
}
return 0;
}
树状数组
前缀和
有一个长度为 n 的序列 A[1], A[2], …, A[n]
每次给出一个询问 (x, y):
请你求出 A[x .. y] 中出现过的数字之和。(出现多次的数只计算一次)
n <= 30000, Q <= 100000
思路:
1.无法使用线段树,因为回溯点的时候无法合并。
2.可以使用桶排暴力的方式。
3.还有一种思路,记录一个数组 left[i],表示左边第一个出现的相同数字 a[i] 的下标。
这样如果 left[i] < x,就说明 a[i] 是 [x, y] 中第一个出现的 a[i].
如果 left[i] >=x,就说明在 [x, i - 1] 中已经出现过一次 a[i]了,不用累计进答案。
处理left数组的时候需要用到离散化或map。
二维前缀和
sum [i] [j]=sum [i-1] [j]+sum [i] [j-1]-sum [i-1] [j-1]+a [i] [j] 递推公式
例:以(x1,y1)为左上角 (x2,y2)为右下角的前缀和:
S(x1,y1,x2,y2)=sum[x2] [y2]-sum[x1] [y2]-sum[x2] [y1]+sum[x1-1] [y2-1]; 注意边界
树状数组只能用于单点修改
树状数组的思想:
元素个数的二进制就是下标的二进制表示中最低位的1 所在的位置对应的数。
Lowbit(x):
树状数组的查询:
ans = 0
while (i > 0) ans += sum[i], i -= C(i);
树状数组修改:与查询不同的是,这里是每一步循环给下标加上 C(i)
change(i, v):
while(i <= n) sum[i] += v, i += C(i)
例1:二维平面上有 n 个点 (x[i], y[i])。现在请你求出每个点左下角的点的个数。
n <= 15000, 0 <= x, y <= 32000
分析—把二维数据结构转换为一维数据结构:
注意到在 i 左下角的点也就是满足 x <= x[i], y <= y[i] 的点。
还是运用扫描线的思想,把一维限制直接去掉。
从小到大枚举 y[i],每次都把 y <= y[i] 的点插入一个集合 S。
y已经满足了,但x不一定满足。
故在 S 里查询 x <= x[i] 的个数即可。
例2:给定一个数列 A[1], A[2], …, A[n].
问有多少个有序对 (x, y),满足:
x < y
A[x] >= y
A[y] >= x
n <= 200000
分析:看上去要满足三个条件,实际上我们可以合并前两个得到:
统计 x < y <= A[x] 且 A[y] >= x 的数对。
通过对一维排序,按顺序处理,来满足这维要求。
然后统计第二维的信息即可。
枚举x,从大到小维护y
若a[y]>=x,标记此y点
最后只需要查询从x到a[x]区间内有多少标记即可。
例3:二维平面上有 n 个点 (x[i], y[i])。
现在请你求出每个点左下角的点的个数。
n <= 15000, 0 <= x, y <= 32000
注意到在 i 左下角的点也就是满足 x <= x[i], y <= y[i] 的点。
还是运用扫描线的思想,把一维限制直接去掉。
从小到大枚举 y[i],每次都把 y <= y[i] 的点插入一个集合 S。
然后在 S 里查询 x <= x[i] 的个数即可。
具体来说,我们从小到大枚举 y 坐标。
每次把 y 坐标小于等于当前枚举值的点的横坐标 x 插入 S 集合。
对于一个点 (x[i], y[i]) (y[i]等于当前枚举的y坐标),它左下角的点的个数等于 S 中小于等于 x[i] 的个数。
只需要用树状数组来维护 S 集合中的数。
插入一个 x,就把 add(x, 1)
查询的时候,把 query(x[i]) 加入答案即可。
时间复杂度是 O(n log n)。
Map
映射,把它看做一个无限大的数组。
定义方式:map<int ,int> a;
使用方式:a[x]++,cout<<a[y]等。
利用迭代器查询map里的所有二元组:
for (map<int,int>::iterator sit=a.begin(); sit!=a.end(); sit++) cout<
清空:a.clear();
Hash
解决哈希冲突的办法:
1.挂链组。
2.将重复的y向上移,若想查找只需要找原来位置是否为y,向上找即可。
3.第一次重复向上移一位,后移两位,四位等。避免冲突频率。
字符串哈希
用数字代表字符串中的字母,比较两者之间的哈希值即可比较两字符串是否相同。
好处:可以同时比较多个字符串。
KMP
有了字串的hash值,在字符串中找长度为m的子字符串的个数。
Set
定义:set
实现方式:红黑树。
插入元素:a.insert(100);
清空set:a.clear();
查询set中有多少元素:a.size();
查询首元素:a.begin(),返回iterator。
查询最后一个元素+1:a.end(),返回iterator。
删除:a.erase(sit); sit是一个iterator类型的指针或者是元素值。
判断是否有数字100:a.count(100),返回bool值。用二叉树的遍历就可以实现。
从小到大遍历set:
for (set
注:加粗部分的复杂度为O(logn),相当于去找下一个子节点。
例:宠物领养场
凡凡开了一间宠物收养场。收养场提供两种服务:收养被主人遗弃的宠物和让新的主人领养这些宠物。
每个领养者都希望领养到自己满意的宠物,凡凡根据领养者的要求通过他自己发明的一个特殊的公式,得出该领养者希望领养的宠物的特点值a(a是一个正整数,a<2^31),而他也给每个处在收养场的宠物一个特点值。这样他就能够很方便的处理整个领养宠物的过程了,宠物收养场总是会有两种情况发生:被遗弃的宠物过多或者是想要收养宠物的人太多,而宠物太少。
被遗弃的宠物过多时,假若到来一个领养者,这个领养者希望领养的宠物的特点值为a,那么它将会领养一只目前未被领养的宠物中特点值最接近a的一只宠物。(任何两只宠物的特点值都不可能是相同的,任何两个领养者的希望领养宠物的特点值也不可能是一样的)如果有两只满足要求的宠物,即存在两只宠物他们的特点值分别为a-b和a+b,那么领养者将会领养特点值为a-b的那只宠物。
收养宠物的人过多,假若到来一只被收养的宠物,那么哪个领养者能够领养它呢?能够领养它的领养者,是那个希望被领养宠物的特点值最接近该宠物特点值的领养者,如果该宠物的特点值为a,存在两个领养者他们希望领养宠物的特点值分别为a-b和a+b,那么特点值为a-b的那个领养者将成功领养该宠物。
一个领养者领养了一个特点值为a的宠物,而它本身希望领养的宠物的特点值为b,那么这个领养者的不满意程度为abs(a-b)。
你得到了一年当中,领养者和被收养宠物到来收养所的情况,请你计算所有收养了宠物的领养者的不满意程度的总和。这一年初始时,收养所里面既没有宠物,也没有领养者
分析:用lowbound找到一个相近x的元素指针,指针--去找另外一个相近的宠物。
比较x与第一个指针所代表宠物的值的差和第二个指针所代表宠物值的差。
最后删除此元素代表宠物离开宠物店。
s.erase()内可以写指针也可以写值。
常用手写平衡树:Treep,Splay
树状数组求逆序对
一串数字得到后标上序号。
从序号为1的开始讨论,出现一个点就标记到相应的数组位置上。
再往下讨论的时候,看该数右面有多少点被标记了,每有一个被标记就加进逆序对的个数。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号