一、决策树剪枝
(1)目的
剪枝(pruning)是决策树学习算法解决过拟合问题的主要手段。
在决策树学习中,为了尽可能正确分类训练样本,节点划分过程将不断重复,有时会造成决策树分支过多,这时有可能因训练样本学得“太好”了,以至于把训练集自身的一些特点当作所有数据都具有的一般性质而导致过拟合。因此,可通过主动去掉一些分支来降低过拟合的风险。
剪枝策略分为预剪枝(prepruning)和后剪枝(post-pruning)。
(2)手动剪枝
1.剪枝前
使用上一次作业中的数据集(稍作调整):判断特征是否属于我室友sjh。
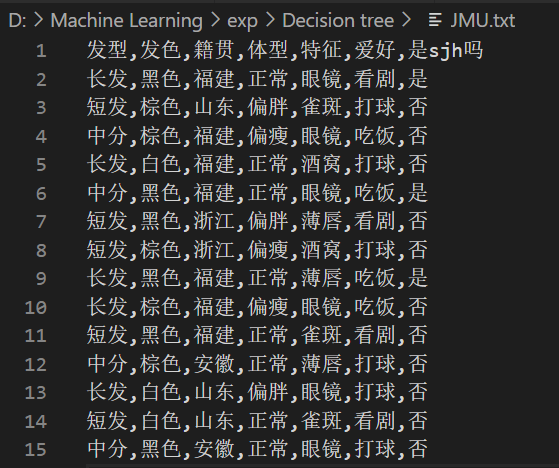
划分训练集和验证集:

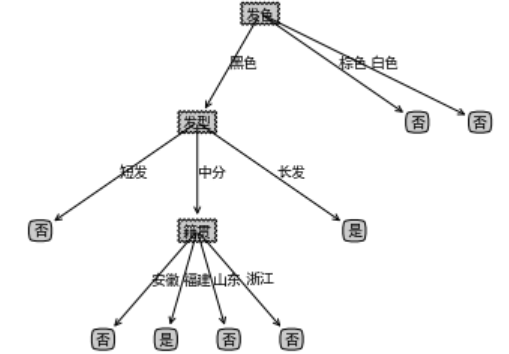
回顾一下剪枝操作前的决策树的样子:
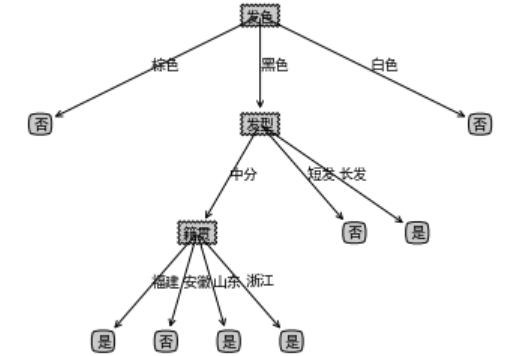
以及数据集当前的信息熵:
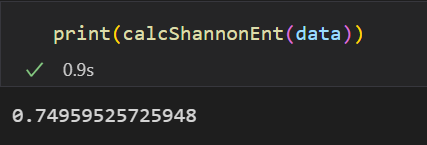
补充:关于缺失值的处理
处理前:
处理后:

def makeTreeFull(myTree, labels_full, default): """ 将树中的不存在的特征标签进行补全,补全为父节点中出现最多的类别 :param myTree: 生成的树 :param labels_full: 特征的全部标签 :param parentClass: 父节点中所含最多的类别 :param default: 如果缺失标签中父节点无法判断类别则使用该值 :return: """ # 这里所说的父节点就是当前根节点,把当前根节点下不存在的特征标签作为子节点 # 拿到当前的根节点 root_key = list(myTree.keys())[0] # 拿到根节点下的所有分类,可能是子节点(好瓜or坏瓜)也可能不是子节点(再次划分的属性值) sub_tree = myTree[root_key] # 如果是叶子节点就结束 if isinstance(sub_tree, str): return # 找到使用当前节点分类下最多的种类,该分类结果作为新特征标签的分类,如:色泽下面没有浅白则用色泽中有的青绿分类作为浅白的分类 root_class = [] # 把已经分好类的结果记录下来 for sub_key in sub_tree.keys(): if isinstance(sub_tree[sub_key], str): root_class.append(sub_tree[sub_key]) # 找到本层出现最多的类别,可能会出现相同的情况取其一 if len(root_class): most_class = collections.Counter(root_class).most_common(1)[0][0] else: most_class = None# 当前节点下没有已经分类好的属性 # print(most_class) # 循环遍历全部特征标签,将不存在标签添加进去 for label in labels_full[root_key]: if label not in sub_tree.keys(): if most_class is not None: sub_tree[label] = most_class else: sub_tree[label] = default # 递归处理 for sub_key in sub_tree.keys(): if isinstance(sub_tree[sub_key], dict): makeTreeFull(myTree=sub_tree[sub_key], labels_full=labels_full, default=default)
2.预剪枝
①概念
预剪枝(pre-pruning):预剪枝就是在构造决策树的过程中,先对每个结点在划分前进行估计,若果当前结点的划分不能带来决策树模型泛化性能的提升,则不对当前结点进行划分并且将当前结点标记为叶结点。
②过程
先计算出所有特征的信息增益值:
调用函数计算信息增益
def chooseBestFeatureToSplit(dataSet, labels): """ 选择最好的数据集划分特征,根据信息增益值来计算 :param dataSet: :return: """ # 得到数据的特征值总数 numFeatures = len(dataSet[0]) - 1 # 计算出基础信息熵 baseEntropy = calcShannonEnt(dataSet) # 基础信息增益为0.0 bestInfoGain = 0.0 # 最好的特征值 bestFeature = -1 # 对每个特征值进行求信息熵 for i in range(numFeatures): # 得到数据集中所有的当前特征值列表 featList = [example[i] for example in dataSet] # 将当前特征唯一化,也就是说当前特征值中共有多少种 uniqueVals = set(featList) # 新的熵,代表当前特征值的熵 newEntropy = 0.0 # 遍历现在有的特征的可能性 for value in uniqueVals: # 在全部数据集的当前特征位置上,找到该特征值等于当前值的集合 subDataSet = splitDataSet(dataSet=dataSet, axis=i, value=value) # 计算出权重 prob = len(subDataSet) / float(len(dataSet)) # 计算出当前特征值的熵 newEntropy += prob * calcShannonEnt(subDataSet) # 计算出“信息增益” infoGain = baseEntropy - newEntropy #print('当前特征值为:' + labels[i] + ',对应的信息增益值为:' + str(infoGain)+"i等于"+str(i)) #如果当前的信息增益比原来的大 if infoGain > bestInfoGain: # 最好的信息增益 bestInfoGain = infoGain # 新的最好的用来划分的特征值 bestFeature = i #print('信息增益最大的特征为:' + labels[bestFeature]) return bestFeature
打印结果返回信息增益值最大的三个特征:发色、籍贯和发型

先选择发型来对数据集进行划分,这会产生三个分支,如下图所示:
 但因为是预剪枝,所以要判断是否应该进行这个划分,判断的标准就是看划分前后的泛化性能是否有提升,也就是如果划分后泛化性能有提升,则划分;否则,不划分。
但因为是预剪枝,所以要判断是否应该进行这个划分,判断的标准就是看划分前后的泛化性能是否有提升,也就是如果划分后泛化性能有提升,则划分;否则,不划分。
下面来看看是否要用发型进行划分,划分前:所有样本都在根节点,把该结点标记为叶节点,其类别标记为训练集中样本数量最多的类别,然后用验证集对其性能评估,可以看出样本{13,14}被正确分类,其他被错误分类,因此精度为50%。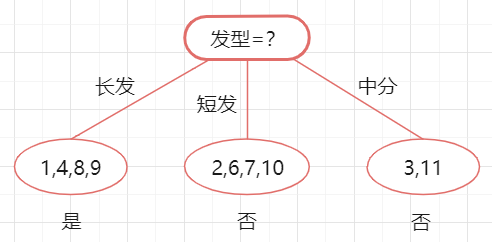
划分后: 划分后的的决策树如下,很明显,验证集上只有14被分类错误,其余三个样例都分类正确。此时精度是3/4 = 75% > 50%。所以,我们可以用发型进行划分。
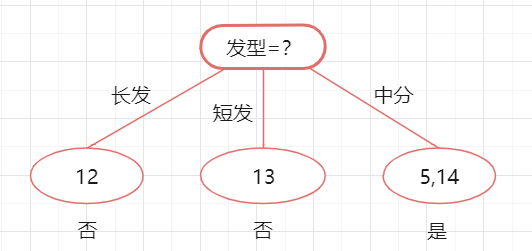
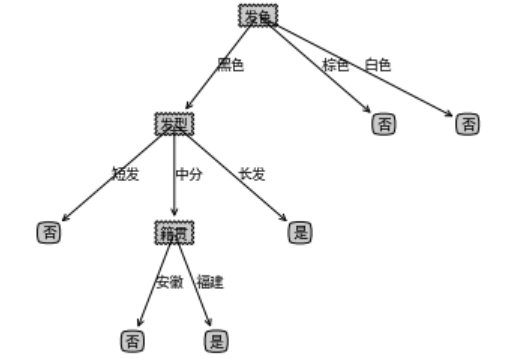
接下来,决策树算法对结点 ②进行划分,再次使用信息增益挑选出值最大的那个特征,信息增益值最大的特征是“发色”,则使用发色划分后决策树为:

计算方法和上面类似所以略过
依旧用验证集进行计算,划分后精度为:3/4=75%=75%,因此可以划分结点 ②。
下一步划分最优的属性为“籍贯”,划分后验证集精度为100%>75%,因此这个划分也可以提升验证集精度,允许划分。
所以基于预剪枝策略生成的最终的决策树为:
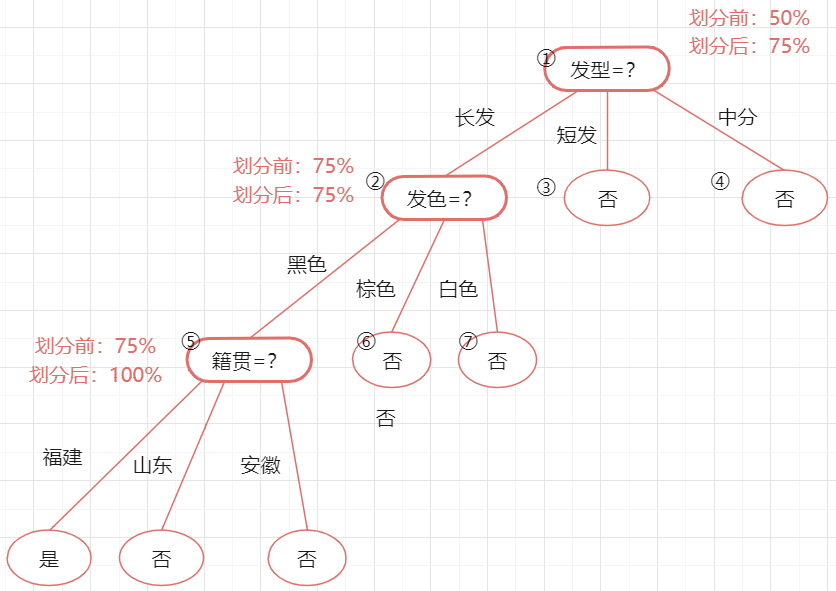
3.后剪枝
①概念
后剪枝(post-pruning)是先从训练集生成一棵完整的决策树,然后自底向上地对非叶结点进行考察,若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升,则将该子树替换为叶结点。
②过程
先整理一下剪枝前的决策树:
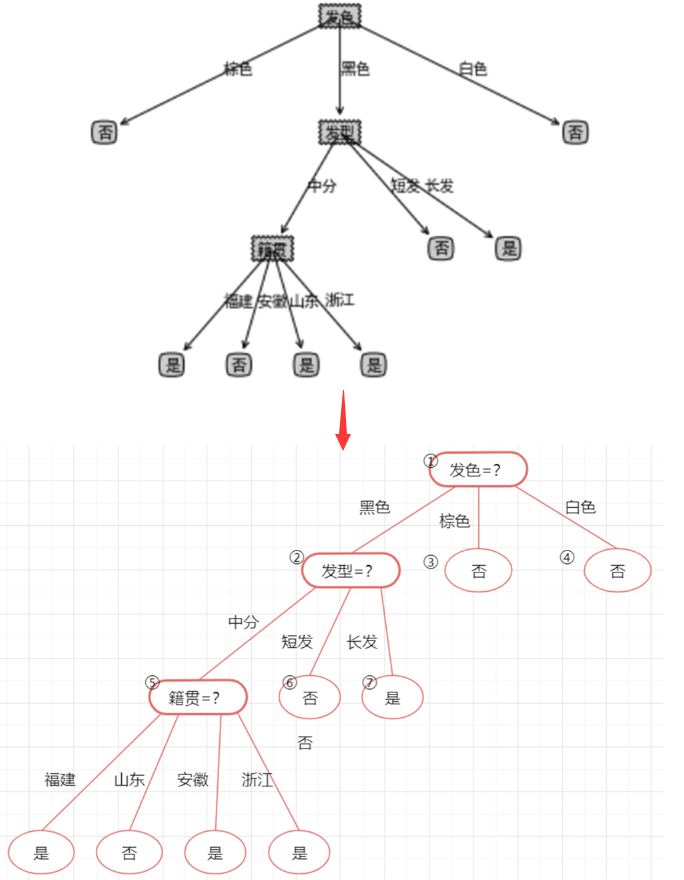
代入验证集的数据,易知该决策树的验证集精度为3/4=75%。后剪枝首先考察上图中的结点⑤,若将其领衔的分支剪除,则相当于把②替换为叶结点。
替换后的叶结点未包含训练样本,选择将其类别标记为"是":
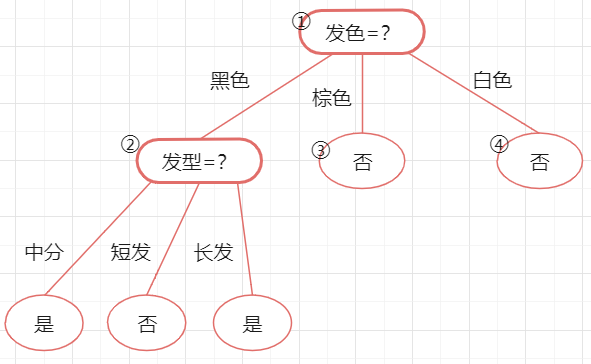
此时决策树的验证集精度仍为3/4=75%。于是,后剪枝策略决定不进行剪枝。
然后考察结点②,若将其领衔的子树替换为叶结点,则替换后的叶结点包含编号为{1,6,8,10} 的训练样例,叶结点标记为"是"。
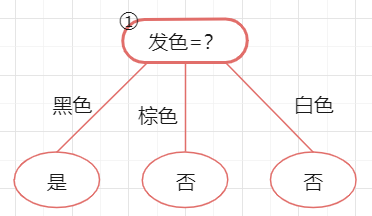
此时决策树的验证集精度仍为3/4=75%。于是,后剪枝策略决定不进行剪枝。
最后考察结点①,若将其领衔的子树替换为叶结点,则此时决策树的验证集精度为初始值75%。于是,后剪枝策略决定不进行剪枝。
最终,基于后剪枝策略所生成的决策树如下图所示,其验证集精度为75%(由于验证集选的不好,导致后剪枝没有变化,以后有时间重新划验证集再试一下)
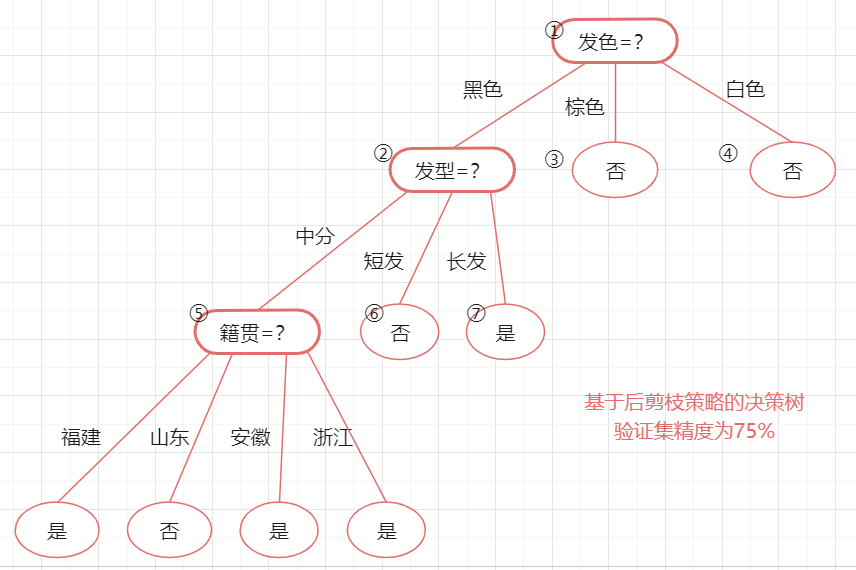
(3)python代码实现剪枝
(已在文章末尾附此部分完整代码压缩包链接)
1.剪枝前

# 决策树可视化 import matplotlib.pyplot as plt # 支持中文 plt.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文 plt.rcParams['axes.unicode_minus'] = False # 显示负号 decisionNodeStyle = dict(boxstyle = "sawtooth", fc = "0.8") leafNodeStyle = {"boxstyle": "round4", "fc": "0.8"} arrowArgs = {"arrowstyle": "<-"} # 画节点 def plotNode(nodeText, centerPt, parentPt, nodeStyle): createPlot.ax1.annotate(nodeText, xy = parentPt, xycoords = "axes fraction", xytext = centerPt , textcoords = "axes fraction", va = "center", ha="center", bbox = nodeStyle, arrowprops = arrowArgs) # 添加箭头上的标注文字 def plotMidText(centerPt, parentPt, lineText): xMid = (centerPt[0] + parentPt[0]) / 2.0 yMid = (centerPt[1] + parentPt[1]) / 2.0 createPlot.ax1.text(xMid, yMid, lineText) # 画树 def plotTree(decisionTree, parentPt, parentValue): # 计算宽与高 leafNum, treeDepth = getTreeSize(decisionTree) # 在 1 * 1 的范围内画图,因此分母为 1 # 每个叶节点之间的偏移量 plotTree.xOff = plotTree.figSize / (plotTree.totalLeaf - 1) # 每一层的高度偏移量 plotTree.yOff = plotTree.figSize / plotTree.totalDepth # 节点名称 nodeName = list(decisionTree.keys())[0] # 根节点的起止点相同,可避免画线;如果是中间节点,则从当前叶节点的位置开始, # 然后加上本次子树的宽度的一半,则为决策节点的横向位置 centerPt = (plotTree.x + (leafNum - 1) * plotTree.xOff / 2.0, plotTree.y) # 画出该决策节点 plotNode(nodeName, centerPt, parentPt, decisionNodeStyle) # 标记本节点对应父节点的属性值 plotMidText(centerPt, parentPt, parentValue) # 取本节点的属性值 treeValue = decisionTree[nodeName] # 下一层各节点的高度 plotTree.y = plotTree.y - plotTree.yOff # 绘制下一层 for val in treeValue.keys(): # 如果属性值对应的是字典,说明是子树,进行递归调用; 否则则为叶子节点 if type(treeValue[val]) == dict: plotTree(treeValue[val], centerPt, str(val)) else: plotNode(treeValue[val], (plotTree.x, plotTree.y), centerPt, leafNodeStyle) plotMidText((plotTree.x, plotTree.y), centerPt, str(val)) # 移到下一个叶子节点 plotTree.x = plotTree.x + plotTree.xOff # 递归完成后返回上一层 plotTree.y = plotTree.y + plotTree.yOff # 画出决策树 def createPlot(decisionTree): fig = plt.figure(1, facecolor = "white") fig.clf() axprops = {"xticks": [], "yticks": []} createPlot.ax1 = plt.subplot(111, frameon = False, **axprops) # 定义画图的图形尺寸 plotTree.figSize = 1.5 # 初始化树的总大小 plotTree.totalLeaf, plotTree.totalDepth = getTreeSize(decisionTree) # 叶子节点的初始位置x 和 根节点的初始层高度y plotTree.x = 0 plotTree.y = plotTree.figSize plotTree(decisionTree, (plotTree.figSize / 2.0, plotTree.y), "") plt.show() # 使用数据测试函数 cxrData, cxrLabel, cxrName = createDataCXR() cxrTree = createTree(cxrData, cxrLabel, cxrName, method = 'id3') print(cxrTree) createPlot(cxrTree)
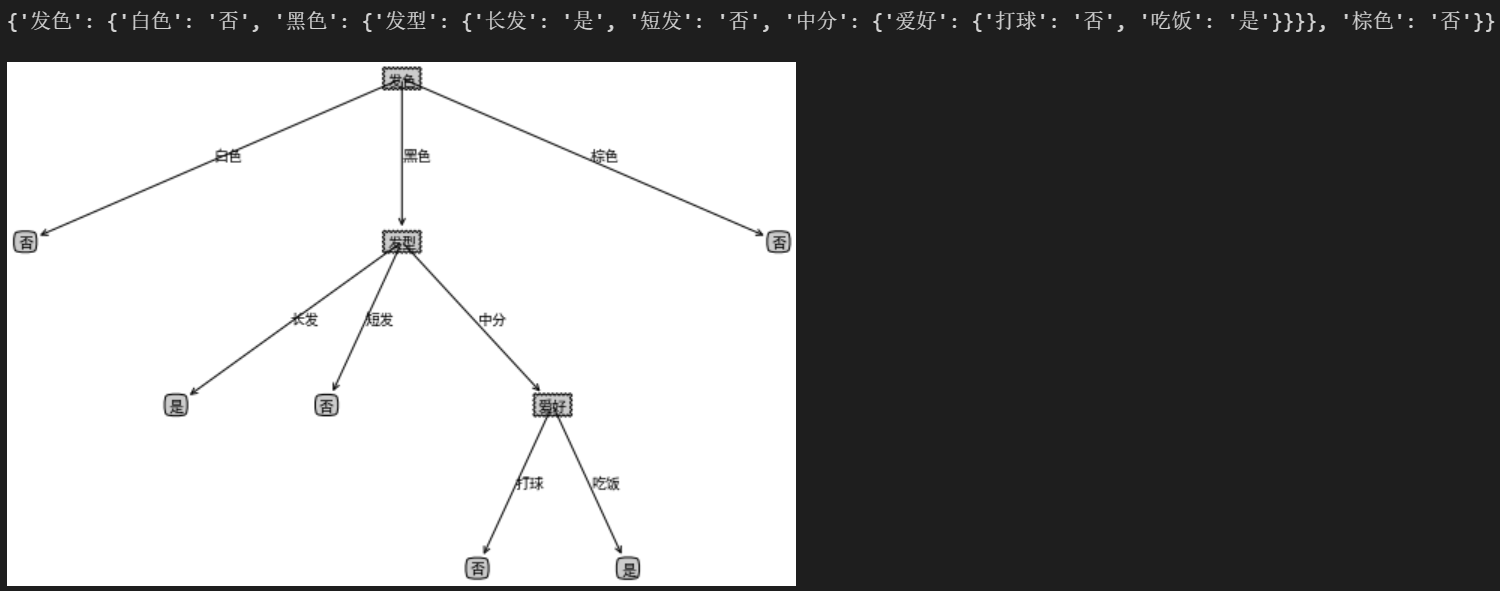
2.预剪枝

# 创建预剪枝决策树 def createTreePrePruning(dataTrain, labelTrain, dataTest, labelTest, names, method = 'id3'): trainData = np.asarray(dataTrain) labelTrain = np.asarray(labelTrain) testData = np.asarray(dataTest) labelTest = np.asarray(labelTest) names = np.asarray(names) # 如果结果为单一结果 if len(set(labelTrain)) == 1: return labelTrain[0] # 如果没有待分类特征 elif trainData.size == 0: return voteLabel(labelTrain) # 其他情况则选取特征 bestFeat, bestEnt = bestFeature(dataTrain, labelTrain, method = method) # 取特征名称 bestFeatName = names[bestFeat] # 从特征名称列表删除已取得特征名称 names = np.delete(names, [bestFeat]) # 根据最优特征进行分割 dataTrainSet, labelTrainSet = splitFeatureData(dataTrain, labelTrain, bestFeat) # 预剪枝评估 # 划分前的分类标签 labelTrainLabelPre = voteLabel(labelTrain) labelTrainRatioPre = equalNums(labelTrain, labelTrainLabelPre) / labelTrain.size # 划分后的精度计算 if dataTest is not None: dataTestSet, labelTestSet = splitFeatureData(dataTest, labelTest, bestFeat) # 划分前的测试标签正确比例 labelTestRatioPre = equalNums(labelTest, labelTrainLabelPre) / labelTest.size # 划分后 每个特征值的分类标签正确的数量 labelTrainEqNumPost = 0 for val in labelTrainSet.keys(): labelTrainEqNumPost += equalNums(labelTestSet.get(val), voteLabel(labelTrainSet.get(val))) + 0.0 # 划分后 正确的比例 labelTestRatioPost = labelTrainEqNumPost / labelTest.size # 如果没有评估数据 但划分前的精度等于最小值0.5 则继续划分 if dataTest is None and labelTrainRatioPre == 0.5: decisionTree = {bestFeatName: {}} for featValue in dataTrainSet.keys(): decisionTree[bestFeatName][featValue] = createTreePrePruning(dataTrainSet.get(featValue), labelTrainSet.get(featValue) , None, None, names, method) elif dataTest is None: return labelTrainLabelPre # 如果划分后的精度相比划分前的精度下降, 则直接作为叶子节点返回 elif labelTestRatioPost < labelTestRatioPre: return labelTrainLabelPre else : # 根据选取的特征名称创建树节点 decisionTree = {bestFeatName: {}} # 对最优特征的每个特征值所分的数据子集进行计算 for featValue in dataTrainSet.keys(): decisionTree[bestFeatName][featValue] = createTreePrePruning(dataTrainSet.get(featValue), labelTrainSet.get(featValue) , dataTestSet.get(featValue), labelTestSet.get(featValue) , names, method) return decisionTree # 将数据集分割为测试集和训练集 cxrDataTrain, cxrLabelTrain, cxrDataTest, cxrLabelTest = splitCxrData(cxrData, cxrLabel) # 生成不剪枝的树 cxrTreeTrain = createTree(cxrDataTrain, cxrLabelTrain, cxrName, method = 'id3') # 生成预剪枝的树 cxrTreePrePruning = createTreePrePruning(cxrDataTrain, cxrLabelTrain, cxrDataTest, cxrLabelTest, cxrName, method = 'id3') # 画剪枝前的树 print("剪枝前的树") createPlot(cxrTreeTrain) # 画剪枝后的树 print("剪枝后的树") createPlot(cxrTreePrePruning)
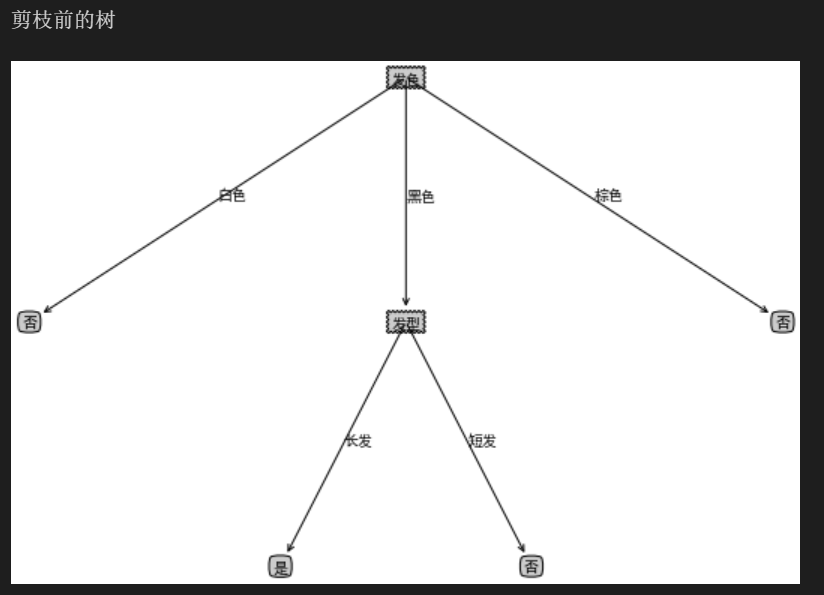
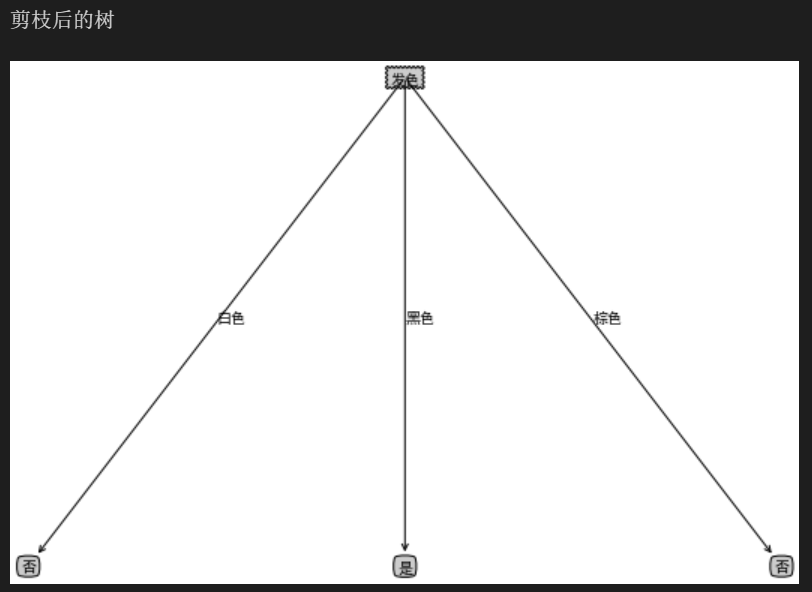
3.后剪枝

#后剪枝 # 创建决策树 带预划分标签 def createTreeWithLabel(data, labels, names, method = 'id3'): data = np.asarray(data) labels = np.asarray(labels) names = np.asarray(names) # 如果不划分的标签为 votedLabel = voteLabel(labels) # 如果结果为单一结果 if len(set(labels)) == 1: return votedLabel # 如果没有待分类特征 elif data.size == 0: return votedLabel # 其他情况则选取特征 bestFeat, bestEnt = bestFeature(data, labels, method = method) # 取特征名称 bestFeatName = names[bestFeat] # 从特征名称列表删除已取得特征名称 names = np.delete(names, [bestFeat]) # 根据选取的特征名称创建树节点 划分前的标签votedPreDivisionLabel=_vpdl decisionTree = {bestFeatName: {"_vpdl": votedLabel}} # 根据最优特征进行分割 dataSet, labelSet = splitFeatureData(data, labels, bestFeat) # 对最优特征的每个特征值所分的数据子集进行计算 for featValue in dataSet.keys(): decisionTree[bestFeatName][featValue] = createTreeWithLabel(dataSet.get(featValue), labelSet.get(featValue), names, method) return decisionTree # 将带预划分标签的tree转化为常规的tree # 函数中进行的copy操作,原因见有道笔记 【YL20190621】关于Python中字典存储修改的思考 def convertTree(labeledTree): labeledTreeNew = labeledTree.copy() nodeName = list(labeledTree.keys())[0] labeledTreeNew[nodeName] = labeledTree[nodeName].copy() for val in list(labeledTree[nodeName].keys()): if val == "_vpdl": labeledTreeNew[nodeName].pop(val) elif type(labeledTree[nodeName][val]) == dict: labeledTreeNew[nodeName][val] = convertTree(labeledTree[nodeName][val]) return labeledTreeNew # 后剪枝 训练完成后决策节点进行替换评估 这里可以直接对xgTreeTrain进行操作 def treePostPruning(labeledTree, dataTest, labelTest, names): newTree = labeledTree.copy() dataTest = np.asarray(dataTest) labelTest = np.asarray(labelTest) names = np.asarray(names) # 取决策节点的名称 即特征的名称 featName = list(labeledTree.keys())[0] # print("\n当前节点:" + featName) # 取特征的列 featCol = np.argwhere(names==featName)[0][0] names = np.delete(names, [featCol]) # print("当前节点划分的数据维度:" + str(names)) # print("当前节点划分的数据:" ) # print(dataTest) # print(labelTest) # 该特征下所有值的字典 newTree[featName] = labeledTree[featName].copy() featValueDict = newTree[featName] featPreLabel = featValueDict.pop("_vpdl") # print("当前节点预划分标签:" + featPreLabel) # 是否为子树的标记 subTreeFlag = 0 # 分割测试数据 如果有数据 则进行测试或递归调用 np的array我不知道怎么判断是否None, 用is None是错的 dataFlag = 1 if sum(dataTest.shape) > 0 else 0 if dataFlag == 1: # print("当前节点有划分数据!") dataTestSet, labelTestSet = splitFeatureData(dataTest, labelTest, featCol) for featValue in featValueDict.keys(): # print("当前节点属性 {0} 的子节点:{1}".format(featValue ,str(featValueDict[featValue]))) if dataFlag == 1 and type(featValueDict[featValue]) == dict: subTreeFlag = 1 # 如果是子树则递归 newTree[featName][featValue] = treePostPruning(featValueDict[featValue], dataTestSet.get(featValue), labelTestSet.get(featValue), names) # 如果递归后为叶子 则后续进行评估 if type(featValueDict[featValue]) != dict: subTreeFlag = 0 # 如果没有数据 则转换子树 if dataFlag == 0 and type(featValueDict[featValue]) == dict: subTreeFlag = 1 # print("当前节点无划分数据!直接转换树:"+str(featValueDict[featValue])) newTree[featName][featValue] = convertTree(featValueDict[featValue]) # print("转换结果:" + str(convertTree(featValueDict[featValue]))) # 如果全为叶子节点, 评估需要划分前的标签,这里思考两种方法, # 一是,不改变原来的训练函数,评估时使用训练数据对划分前的节点标签重新打标 # 二是,改进训练函数,在训练的同时为每个节点增加划分前的标签,这样可以保证评估时只使用测试数据,避免再次使用大量的训练数据 # 这里考虑第二种方法 写新的函数 createTreeWithLabel,当然也可以修改createTree来添加参数实现 if subTreeFlag == 0: ratioPreDivision = equalNums(labelTest, featPreLabel) / labelTest.size equalNum = 0 for val in labelTestSet.keys(): equalNum += equalNums(labelTestSet[val], featValueDict[val]) ratioAfterDivision = equalNum / labelTest.size # print("当前节点预划分标签的准确率:" + str(ratioPreDivision)) # print("当前节点划分后的准确率:" + str(ratioAfterDivision)) # 如果划分后的测试数据准确率低于划分前的,则划分无效,进行剪枝,即使节点等于预划分标签 # 注意这里取的是小于,如果有需要 也可以取 小于等于 if ratioAfterDivision < ratioPreDivision: newTree = featPreLabel return newTree
# 按照之前手动画的决策树模型 cxrTreeBeforePostPruning = {"发色": {"_vpdl": "是" , '黑色': {'发型':{"_vpdl": "是" , '中分': {'籍贯': {"_vpdl": "是" , '福建': '是' , '山东': '否' , '安徽': '是' , '浙江': '是'}} , '短发': '否' , '长发': '是'}} , '棕色': '否' , '白色': '否'}} cxrTreePostPruning = treePostPruning(cxrTreeBeforePostPruning, cxrDataTest, cxrLabelTest, cxrName) createPlot(convertTree(cxrTreeBeforePostPruning)) createPlot(cxrTreePostPruning)
最后得到的结果与前面手动剪枝的结果相同(后剪枝确实没变化,看来我手动没画错,是验证集真的选的不行......)
剪枝前后对比:
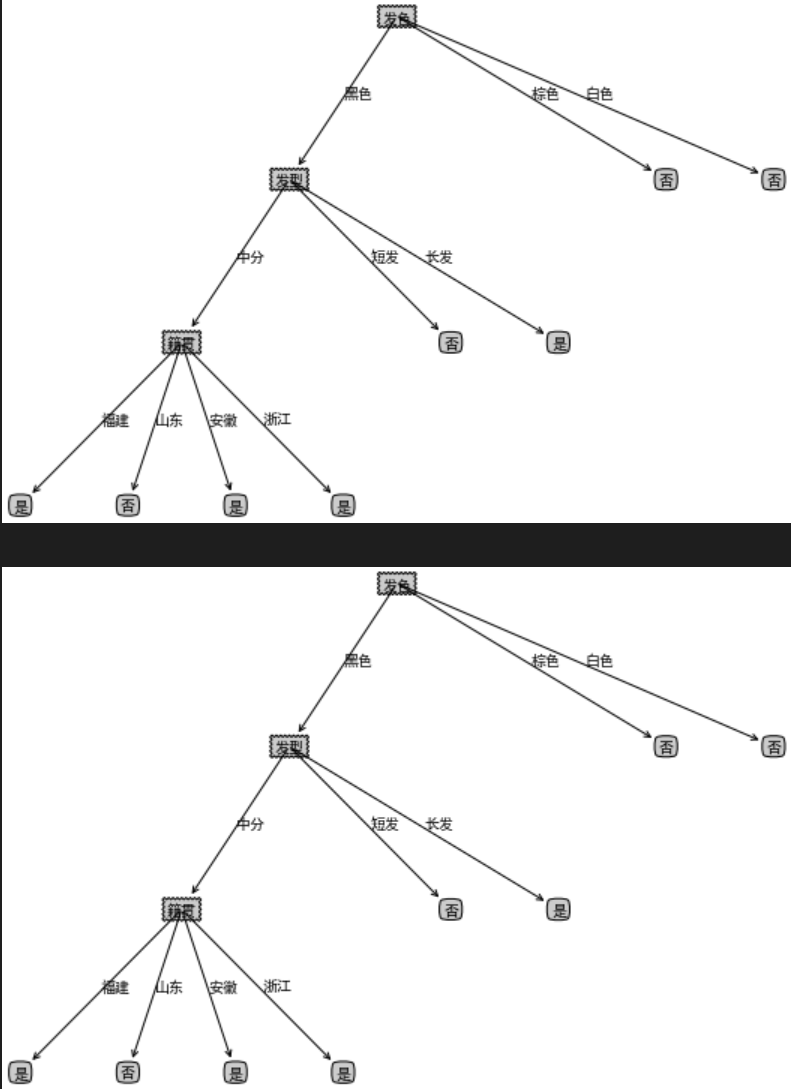
(4)总结
后剪枝决策树通常比预剪枝决策树保留了更多的分支。一般情形下,后剪枝决策树的欠拟合风险很小,泛化性能往往优于预剪枝决策树。但后剪枝过程是在生成完全决策树之后进行的,并且要自底向上地对树中的所有非叶结点进行逐一考察,因此其训练时间开销比未剪枝决策树和预剪枝决策树都要大得多。
二、knn与决策树对比
KNN算法,对于数值型的数据适配度比较高,且预处理较少,一般单一类数据归一化即可,选择求距离的公式也可以依托实际进行。KNN有算法的一个优点为对异常值不敏感,但是在预处理的时候,如果能将极端数据去掉后再进行归一化,分类效果会更好。
决策树算法对于数据预处理要求高一点,需要预分类,分类过程如果面向问题本身会更加好,用于制作实际算法投入运用的话,由用户来进行一个标度效果对于特定用户本身会更好。但是数据过多的时候,决策树剪枝方面要多进行考虑,但是势必带来准确度降低。
=============================
源码链接:
https://pan.baidu.com/s/1ndOIhy_3euXdShnToGPj4g 提取码: cxr6




 浙公网安备 33010602011771号
浙公网安备 33010602011771号