一、决策树的概述
1.定义
决策树(Decision Tree)是在已知各种情况发生概率的基础上,通过构成决策树来求取净现值的期望值大于等于零的概率,评价项目风险,判断其可行性的决策分析方法,是直观运用概率分析的一种图解法。
决策树是一种树形结构,其中每个内部节点表示一个属性上的测试,每个分支代表一个测试输出,每个叶节点代表一种类别。
策略:“分而治之”
2.决策树的节点
决策树的节点分为内部节点(绿色)和叶节点(蓝色),如下图:
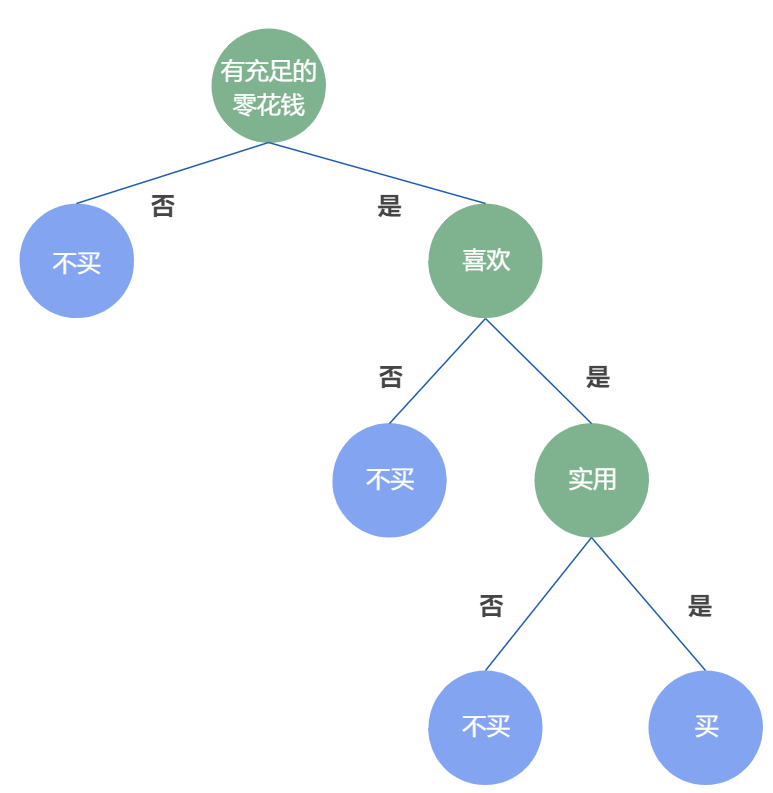
内部节点代表一个特征或属性,叶节点代表一个类。
3.特点
①对属性进行“测试”即对就决策过程中的问题进行判定
②决策树上的每条路径都是一个判定测试序列
其最终学习目的是为了产生一颗泛化能力强即能够有效处理未知样本的决策树。
4.if-then规则
①由决策树的根 节点到叶节点的每一条路径构建一 条规则;
②路径上内部节点的特征对应着规则的条件,而叶节点的类标签对应着规则的结论。
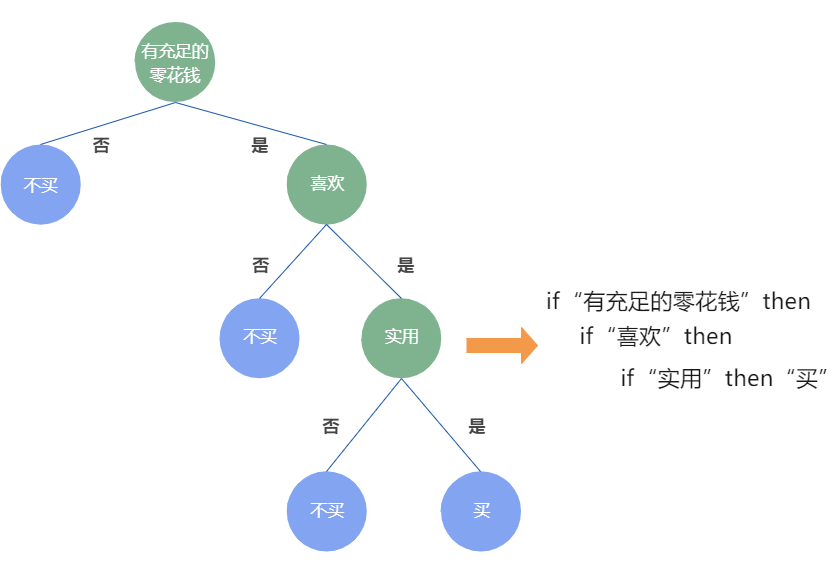
互斥并且完备:每一个实例都被有且仅有一条路径或一条规则所覆盖。
5.优缺点
优点: 列出了决策问题的全部可行方案和可能出现的各种自然状态,以及各可行方法在各种不同状态下的期望值; 能直观地显示整个决策问题在时间和决策顺序上不同阶段的决策过程; 在应用于复杂的多阶段决策时,阶段明显,层次清楚。
缺点: 使用范围有限,无法适用于一些不能用数量表示的决策; 对各种方案的出现概率的确定有时主观性较大,可能导致决策失误。
二、决策树的构建
1.基本流程
(1) 收集数据:可以使用任何方法。
(2) 准备数据:树构造算法只是用于标称型数据,因此数值型数据必须离散化。
(3) 分析数据:可以使用任何方法,决策树构造完成后,可以检查决策树图形是否符合预期。
(4) 训练算法:构造一个决策树的数据结构。
(5) 测试算法:使用经验树计算错误率。当错误率达到可接收范围,此决策树就可投放使用。
(6) 使用算法:此步骤可以使用适用于任何监督学习算法,而使用决策树可以更好地理解数据的内在含义。
2.划分选择
如何选择最优划分属性:
①信息增益
信息熵:度量样本集合纯度的指标之一,信息熵(Ent(D))的值越小,则样本集合(D)的纯度越高,Ent(D)最小为0,最大值为log2|y|。
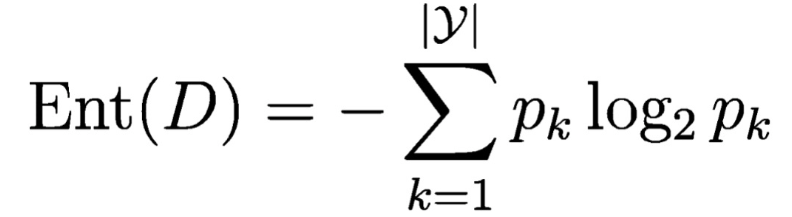
信息熵的代码实现:
def calcShannonEnt(dataSet): numEntries = len(dataSet) labelCounts = {}#字典 for featVec in dataSet: #the the number of unique elements and their occurance currentLabel = featVec[-1] #扩展字典添加新键值 if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0 labelCounts[currentLabel] += 1#统计键值出现的次数 shannonEnt = 0.0 for key in labelCounts: prob = float(labelCounts[key])/numEntries#统计某一键值出现频率 shannonEnt -= prob * log(prob,2) #log base 2 return shannonEnt
信息增益的数学表示:
![]()
信息增益应该代表“信息熵的变化量”,故前面的Ent(D)是“划分前的信息熵”,而后面的![]() 是划分之后,各分支的信息熵乘以权重的总和,即“划分后的总信息熵”。
是划分之后,各分支的信息熵乘以权重的总和,即“划分后的总信息熵”。
信息增益的意义:
信息增益越大,意味着使用a来划分所获得的“纯度提升”越大。因此可以用信息增益可以作为选择决策树划分属性的判断依据。
信息增益公式的代码实现:
baseEntropy = calcShannonEnt(dataSet)#得到总熵值 #得到每种决策属性的比例 prob = len(subDataSet)/float(len(dataSet)) #得到各个特征值对应的熵 newEntropy += prob * calcShannonEnt(subDataSet)
- python的列表推导式:[表达式 for 变量 in 列表]
- 利用set集合的性质取出列表中的重复元素,得到某一属性的分类标签列表
def chooseBestFeatureToSplit(dataSet): numFeatures = len(dataSet[0]) - 1 baseEntropy = calcShannonEnt(dataSet)#得到总熵值 bestInfoGain = 0.0; bestFeature = -1 for i in range(numFeatures): featList = [example[i] for example in dataSet] #利用set内值不重复的性质得到某一属性的分类标签列表 uniqueVals = set(featList) newEntropy = 0.0 #遍历特征值得到相应的数据集 for value in uniqueVals: subDataSet = splitDataSet(dataSet, i, value) #得到每种决策属性的比例 prob = len(subDataSet)/float(len(dataSet)) #得到各个特征值对应的熵 newEntropy += prob * calcShannonEnt(subDataSet) #计算信息增益 infoGain = baseEntropy - newEntropy if (infoGain > bestInfoGain): #与最佳值比较 bestInfoGain = infoGain bestFeature = i #返回最优划分属性的索引值 return bestFeature
总结:一般而言,信息增益越大,则意味着该属性越适合作为划分属性;信息增益对可取值数目较多的属性有所偏好。
②增益率
因为信息增益对可取值较多的属性有所偏好,为减少这种偏好可能带来的不利影响,不直接使用信息增益,而使用增益率来选择最优划分属性。
增益率定义:
![]()
其中,
![]()
IV(a)称为属性 a 的“固有值”,属性 a 的可能性取值越多(即 V 越大),则IV(a) 的值通常会越大。
总结:增益率对可取值数目较少的数学有所偏好。在算法实践中可采用一个启发式方法:先从候选划分属性中找到信息增益高于平均水平的属性,再从中选取增益率最大的。
③基尼指数
分类问题中,设D中有K个类,样本点属于第K类的概率为Pk,则概率分布的基尼值定义为:
![]()
给定数据集D,属性a的基尼指数定义为:
![]()
总结:Gini(D)越小,数据集D的纯度越高,因此在选择划分属性时,选择使得划分后基尼指数最小的属性作为最优划分属性。
基尼系数代码实现:
# 计算某一维度相对于标签的基尼指数 def Gini(self, y): size = len(y) # 数据集大小 gini_total = 0 classes_idx_num = dict(Counter(y)) # 统计每类标签下包含的数据个数 # 计算基尼系数: for key in classes_idx_num.keys(): # 计算第key个标签的基尼系数分量 prob = classes_idx_num[key] / size # 用出现频率表示概率 gini_total += prob * prob return 1 - gini_total # X: 输入数据, size=(batches, features) # y: 类别标签, size=(batches,) # dim: 当前是第几维度 # num_D: 数据总数 def GiniIdx(self, X, y, num_D, dim): a = X[:, dim] # 获取数据第dim维度 v = set(a) # 获取数据第dim维度可能的取值 gini_a = 0 # 计算数据第dim维度的信息增益: for i in v: # 第dim维度第i个取值出现的频率 prob_a_v = np.sum(a==i)/num_D gini_a_v = self.Gini(y[np.where(a==i)]) gini_a += prob_a_v * gini_a_v return gini_a
三、决策树的代码实现
(1)我的数据集
新建JMU.txt文件。
我选择的目标是利用决策树判断特征是否属于我室友sjh。
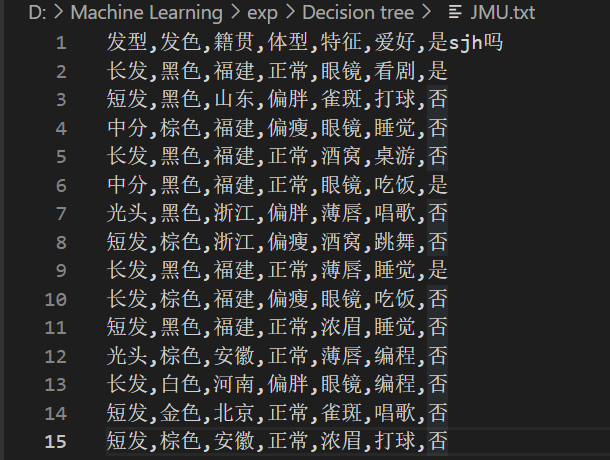
(2)具体python代码
1.导入模块
import numpy as np #用pandas模块的read_csv()函数读取数据文本 import pandas as pd #用numpy模块将dataframe转换为list(列表) import math #用math模块的log2函数计算对数 import collections #用Counter来完成计数
2.导入数据
def import_data(): data = pd.read_csv('D:\Machine Learning\exp\Decision tree\JMU.txt') data.head(10) data=np.array(data).tolist() # 特征值列表 labels = ['发型', '发色', '籍贯', '体型', '特征', '爱好'] # 特征对应的所有可能的情况 labels_full = {} for i in range(len(labels)): labelList = [example[i] for example in data] uniqueLabel = set(labelList) labels_full[labels[i]] = uniqueLabel return data,labels,labels_full data,labels,labels_full=import_data() #调用函数获取数据
3.计算初始的信息熵
def calcShannonEnt(dataSet): #计算给定数据集的信息熵 # 计算出数据集的总数 numEntries = len(dataSet) # 用来统计标签 labelCounts = collections.defaultdict(int) # 循环整个数据集,得到数据的分类标签 for featVec in dataSet: # 得到当前的标签 currentLabel = featVec[-1] # 如果当前的标签不再标签集中,就添加进去 # 标签集中的对应标签数目加一 labelCounts[currentLabel] += 1 # 默认的信息熵 shannonEnt = 0.0 for key in labelCounts: # 计算出当前分类标签占总标签的比例数 prob = float(labelCounts[key]) / numEntries # 以2为底求对数 shannonEnt -= prob * math.log2(prob) return shannonEnt
查看初始信息熵:
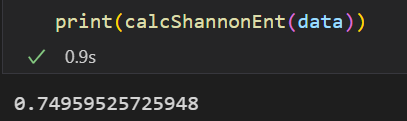
4.获取每个特征值的数量
def splitDataSet(dataSet, axis, value): """ 按照给定的特征值,将数据集划分 :param dataSet: 数据集 :param axis: 给定特征值的坐标 :param value: 给定特征值满足的条件,只有给定特征值等于这个value的时候才会返回 :return: """ # 创建一个新的列表,防止对原来的列表进行修改 retDataSet = [] # 遍历整个数据集 for featVec in dataSet: # 如果给定特征值等于想要的特征值 if featVec[axis] == value: # 将该特征值前面的内容保存起来 reducedFeatVec = featVec[:axis] # 将该特征值后面的内容保存起来,所以将给定特征值给去掉了 reducedFeatVec.extend(featVec[axis + 1:]) # 添加到返回列表中 retDataSet.append(reducedFeatVec) return retDataSet
5.计算信息增益来确定最好的数据集划分

def chooseBestFeatureToSplit(dataSet, labels): """ 选择最好的数据集划分特征,根据信息增益值来计算 :param dataSet: :return: """ # 得到数据的特征值总数 numFeatures = len(dataSet[0]) - 1 # 计算出基础信息熵 baseEntropy = calcShannonEnt(dataSet) # 基础信息增益为0.0 bestInfoGain = 0.0 # 最好的特征值 bestFeature = -1 # 对每个特征值进行求信息熵 for i in range(numFeatures): # 得到数据集中所有的当前特征值列表 featList = [example[i] for example in dataSet] # 将当前特征唯一化,也就是说当前特征值中共有多少种 uniqueVals = set(featList) # 新的熵,代表当前特征值的熵 newEntropy = 0.0 # 遍历现在有的特征的可能性 for value in uniqueVals: # 在全部数据集的当前特征位置上,找到该特征值等于当前值的集合 subDataSet = splitDataSet(dataSet=dataSet, axis=i, value=value) # 计算出权重 prob = len(subDataSet) / float(len(dataSet)) # 计算出当前特征值的熵 newEntropy += prob * calcShannonEnt(subDataSet) # 计算出“信息增益” infoGain = baseEntropy - newEntropy #print('当前特征值为:' + labels[i] + ',对应的信息增益值为:' + str(infoGain)+"i等于"+str(i)) #如果当前的信息增益比原来的大 if infoGain > bestInfoGain: # 最好的信息增益 bestInfoGain = infoGain # 新的最好的用来划分的特征值 bestFeature = i #print('信息增益最大的特征为:' + labels[bestFeature]) return bestFeature
6.判断各个样本集的各个属性是否一致
def judgeEqualLabels(dataSet): # 计算出样本集中共有多少个属性,最后一个为类别 feature_leng = len(dataSet[0]) - 1 # 计算出共有多少个数据 data_leng = len(dataSet) # 标记每个属性中第一个属性值是什么 first_feature = '' # 各个属性集是否完全一致 is_equal = True # 遍历全部属性 for i in range(feature_leng): # 得到第一个样本的第i个属性 first_feature = dataSet[0][i] # 与样本集中所有的数据进行对比,看看在该属性上是否都一致 for _ in range(1, data_leng): # 如果发现不相等的,则直接返回False if first_feature != dataSet[_][i]: return False return is_equal
7.绘制字典类型的决策树

def createTree(dataSet, labels): # 拿到所有数据集的分类标签 classList = [example[-1] for example in dataSet] # 统计第一个标签出现的次数,与总标签个数比较,如果相等则说明当前列表中全部都是一种标签,此时停止划分 if classList.count(classList[0]) == len(classList): return classList[0] # 计算第一行有多少个数据,如果只有一个的话说明所有的特征属性都遍历完了,剩下的一个就是类别标签,或者所有的样本在全部属性上都一致 if len(dataSet[0]) == 1 or judgeEqualLabels(dataSet): # 返回剩下标签中出现次数较多的那个 return majorityCnt(classList) # 选择最好的划分特征,得到该特征的下标 bestFeat = chooseBestFeatureToSplit(dataSet=dataSet, labels=labels) print(bestFeat) # 得到最好特征的名称 bestFeatLabel = labels[bestFeat] print(bestFeatLabel) # 使用一个字典来存储树结构,分叉处为划分的特征名称 myTree = {bestFeatLabel: {}} # 将本次划分的特征值从列表中删除掉 del(labels[bestFeat]) # 得到当前特征标签的所有可能值 featValues = [example[bestFeat] for example in dataSet] # 唯一化,去掉重复的特征值 uniqueVals = set(featValues) # 遍历所有的特征值 for value in uniqueVals: # 得到剩下的特征标签 subLabels = labels[:] subTree = createTree(splitDataSet(dataSet=dataSet, axis=bestFeat, value=value), subLabels) # 递归调用,将数据集中该特征等于当前特征值的所有数据划分到当前节点下,递归调用时需要先将当前的特征去除掉 myTree[bestFeatLabel][value] = subTree return myTree mytree=createTree(data,labels) #调用函数并打印 print(mytree)

8.绘制可视化决策树

#绘制可视化树 import matplotlib.pylab as plt import matplotlib # 能够显示中文 matplotlib.rcParams['font.sans-serif'] = ['SimHei'] matplotlib.rcParams['font.serif'] = ['SimHei'] # 分叉节点,也就是决策节点 decisionNode = dict(boxstyle="sawtooth", fc="0.8") # 叶子节点 leafNode = dict(boxstyle="round4", fc="0.8") # 箭头样式 arrow_args = dict(arrowstyle="<-") def plotNode(nodeTxt, centerPt, parentPt, nodeType): """ 绘制一个节点 :param nodeTxt: 描述该节点的文本信息 :param centerPt: 文本的坐标 :param parentPt: 点的坐标,这里也是指父节点的坐标 :param nodeType: 节点类型,分为叶子节点和决策节点 :return: """ createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction', xytext=centerPt, textcoords='axes fraction', va="center", ha="center", bbox=nodeType, arrowprops=arrow_args) def getNumLeafs(myTree): """ 获取叶节点的数目 :param myTree: :return: """ # 统计叶子节点的总数 numLeafs = 0 # 得到当前第一个key,也就是根节点 firstStr = list(myTree.keys())[0] # 得到第一个key对应的内容 secondDict = myTree[firstStr] # 递归遍历叶子节点 for key in secondDict.keys(): # 如果key对应的是一个字典,就递归调用 if type(secondDict[key]).__name__ == 'dict': numLeafs += getNumLeafs(secondDict[key]) # 不是的话,说明此时是一个叶子节点 else: numLeafs += 1 return numLeafs def getTreeDepth(myTree): """ 得到数的深度层数 :param myTree: :return: """ # 用来保存最大层数 maxDepth = 0 # 得到根节点 firstStr = list(myTree.keys())[0] # 得到key对应的内容 secondDic = myTree[firstStr] # 遍历所有子节点 for key in secondDic.keys(): # 如果该节点是字典,就递归调用 if type(secondDic[key]).__name__ == 'dict': # 子节点的深度加1 thisDepth = 1 + getTreeDepth(secondDic[key]) # 说明此时是叶子节点 else: thisDepth = 1 # 替换最大层数 if thisDepth > maxDepth: maxDepth = thisDepth return maxDepth def plotMidText(cntrPt, parentPt, txtString): """ 计算出父节点和子节点的中间位置,填充信息 :param cntrPt: 子节点坐标 :param parentPt: 父节点坐标 :param txtString: 填充的文本信息 :return: """ # 计算x轴的中间位置 xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0] # 计算y轴的中间位置 yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1] # 进行绘制 createPlot.ax1.text(xMid, yMid, txtString) def plotTree(myTree, parentPt, nodeTxt): """ 绘制出树的所有节点,递归绘制 :param myTree: 树 :param parentPt: 父节点的坐标 :param nodeTxt: 节点的文本信息 :return: """ # 计算叶子节点数 numLeafs = getNumLeafs(myTree=myTree) # 计算树的深度 depth = getTreeDepth(myTree=myTree) # 得到根节点的信息内容 firstStr = list(myTree.keys())[0] # 计算出当前根节点在所有子节点的中间坐标,也就是当前x轴的偏移量加上计算出来的根节点的中心位置作为x轴(比如说第一次:初始的x偏移量为:-1/2W,计算出来的根节点中心位置为:(1+W)/2W,相加得到:1/2),当前y轴偏移量作为y轴 cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff) # 绘制该节点与父节点的联系 plotMidText(cntrPt, parentPt, nodeTxt) # 绘制该节点 plotNode(firstStr, cntrPt, parentPt, decisionNode) # 得到当前根节点对应的子树 secondDict = myTree[firstStr] # 计算出新的y轴偏移量,向下移动1/D,也就是下一层的绘制y轴 plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD # 循环遍历所有的key for key in secondDict.keys(): # 如果当前的key是字典的话,代表还有子树,则递归遍历 if isinstance(secondDict[key], dict): plotTree(secondDict[key], cntrPt, str(key)) else: # 计算新的x轴偏移量,也就是下个叶子绘制的x轴坐标向右移动了1/W plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW # 打开注释可以观察叶子节点的坐标变化 # print((plotTree.xOff, plotTree.yOff), secondDict[key]) # 绘制叶子节点 plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode) # 绘制叶子节点和父节点的中间连线内容 plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key)) # 返回递归之前,需要将y轴的偏移量增加,向上移动1/D,也就是返回去绘制上一层的y轴 plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD def createPlot(inTree): """ 需要绘制的决策树 :param inTree: 决策树字典 :return: """ # 创建一个图像 fig = plt.figure(1, facecolor='white') fig.clf() axprops = dict(xticks=[], yticks=[]) createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) # 计算出决策树的总宽度 plotTree.totalW = float(getNumLeafs(inTree)) # 计算出决策树的总深度 plotTree.totalD = float(getTreeDepth(inTree)) # 初始的x轴偏移量,也就是-1/2W,每次向右移动1/W,也就是第一个叶子节点绘制的x坐标为:1/2W,第二个:3/2W,第三个:5/2W,最后一个:(W-1)/2W plotTree.xOff = -0.5/plotTree.totalW # 初始的y轴偏移量,每次向下或者向上移动1/D plotTree.yOff = 1.0 # 调用函数进行绘制节点图像 plotTree(inTree, (0.5, 1.0), '') # 绘制 plt.show() if __name__ == '__main__': createPlot(mytree)
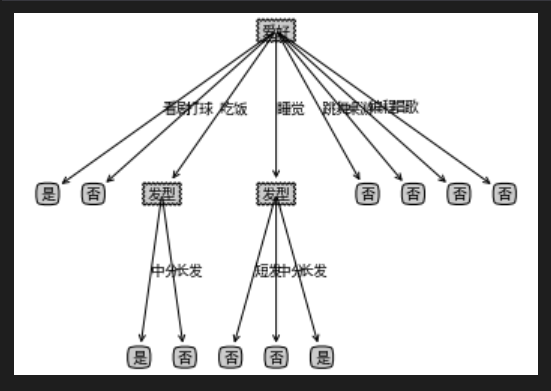
四、小结
本次实验粗糙地实现了简单的决策树的绘制,存在的问题还比较多,感觉数据集做得还不太合理,最后的决策树判断结果和数据及结果不太相符。
后续还需要修改错误,将树中的不存在的特征标签进行补全,以及完成预剪枝、后剪枝以及连续数据的离散化等内容。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号