K-近邻算法

1.简介

K-近邻算法（K-Nearest Neighbor, KNN），属于监督学习,是一中基本分类与回归方法。k 近邻法的输入为实例的特征向量,对应于特征空间的点;输出为实例的类别,可以取多类, k 近邻法假设给定一个训练数据集,其中的实例类别已定,分类时,对新的实例,根据其 k 个最近邻的训练实例的类别,通过多数表决等方式进行预测。

2.基本要素

　　①K值的选择

　　关于k值的选择：一般取一个比较小的数值，例如采用交叉验证法（一部分样本做训练集，一部分做测试集）来选择最优的K值。

　　②距离量度

　　（1）欧氏距离

　　　　

 

 

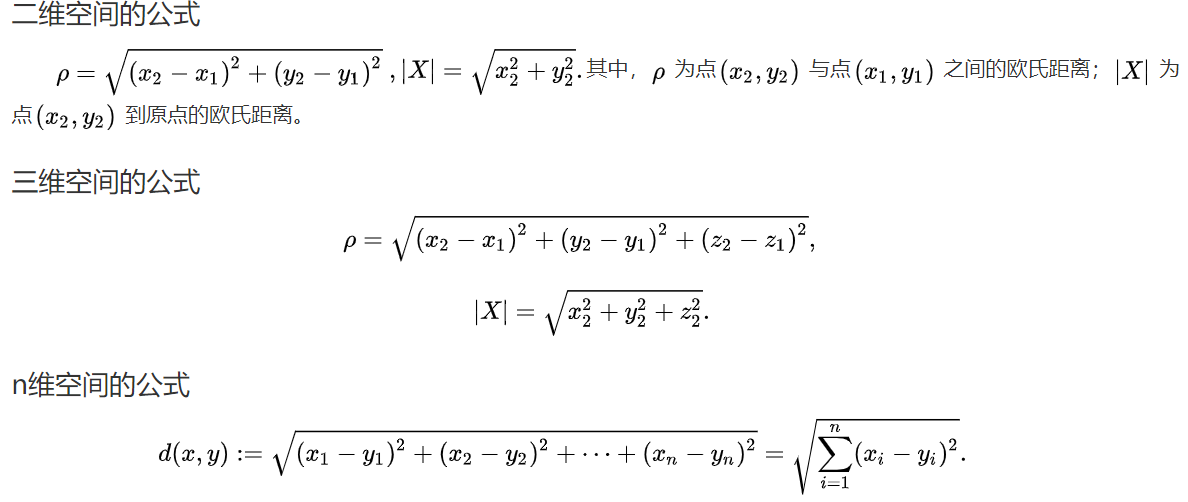
　　（2）曼哈顿距离

　　　　

　　③分类决策规则

　　一般是多数表决,即k个邻居中多的说的算。可以根据不同距离的邻居对该样本产生的影响赋予不同的权重。

3.k近邻算法的优缺点

优点：

①近邻算法是一种在线技术，新数据可以直接加入数据集而不必进行重新训练，

②是k近邻算法理论简单，容易实现。

③准确性高，对异常值和噪声有较高的容忍度。

④k近邻算法天生就支持多分类，区别与感知机、逻辑回归、SVM。

缺点：

①k近邻算法每预测一个“点”的分类都会重新进行一次全局运算，对于样本容量大的数据集计算量比较大。

②样本不平衡时，预测偏差比较大，k值大小的选择得依靠经验或者交叉验证得到。k的选择可以使用交叉验证，也可以使用网格搜索。k的值越大，模型的偏差越大，对噪声数据越不敏感，当 k的值很大的时候，可能造成模型欠拟合。k的值越小，模型的方差就会越大，当 k的值很小的时候，就会造成模型的过拟合。

4.使用k近邻算法的条件

①需要一个训练的数据集，这个数据集包含各种特征值和对应的label值 ,在使用前需要将各种特征值归一化处理。

②利用训练的数据集来对要分类的数据进行分类：

  根据欧式距离计算出要预测的数据与训练数据集中距离最短的前k个值,然后根据前k个值对应的label

  统计出 label值最最多的，如选择的前k个对应的label:['JMU','JMU','JMU','XMU'] ,那么这个结果是JMU类。

  k近邻算法适用于带lable的数值类

5.k近邻算法的一般流程

①收集数据：确定训练样本集合测试数据；

②计算测试数据和训练样本集中每个样本数据的距离；

③按照距离递增的顺序排序；

④选取距离最近的k个点；

⑤确定这k个点中分类信息的频率；

⑥返回前k个点中出现频率最高的分类，作为当前测试数据的分类。

6.应用场景

分类、回归。

线性分类、非线性分类

7.关于knn算法的一段简单代码

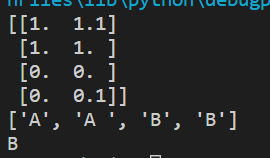
from numpy import *    #NumPy
import operator        #运算符模块
 
def createDataSet():   #这个只是导入数据的函数
     group=array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])  #这个是4行2列的数组
     labels=['A','A ','B','B']
     return group ,labels
 
def classify0 (inX,dataSet,labels,k) : #这个是k近邻算法的实现,要注意传入的参数有哪些.
 #①用于分类的输入向量inX;     ②输入的训练样本集dataSet;     ③标签向量labels;     ④最后的参数k用于选择最近邻居的数目;
     dataSetSize=dataSet.shape[0]               #其中标签向量的元素数目和矩阵dataSet的行数相同
     diffMat=tile(inX,(dataSetSize,1))-dataSet  #diffMat是数组 下面是一些算法(欧式距离的算法)
     sqDiffMat=diffMat**2                       #对数组diffMat的每个元素进行平方
     sqDistances=sqDiffMat.sum(axis=1)          #axis=1,表示的是按行相加. axis=0表示按列相加.
     distances=sqDistances**0.5                 #开平方
     sortedDistIndicies=distances.argsort()     #返回的从小到大的索引
     classCount={}
     for i in range(k):                         
         voteIlabel=labels[sortedDistIndicies[i]]  #确定前k个距离最小的主要分类,sortedDistIndicies[i]返回的是样本的位置
         classCount[voteIlabel]=classCount.get(voteIlabel,0)+1
     sortedClassCount=sorted(classCount.items(),key=operator.itemgetter(1),reverse=True) 
     return sortedClassCount[0][0]              #返回发生频率最高的标签
 
group,labels=createDataSet()
print(group)
print(labels)
 
a=classify0([0,0],group,labels,3)
print(a)

 

8.使用knn算法的例子

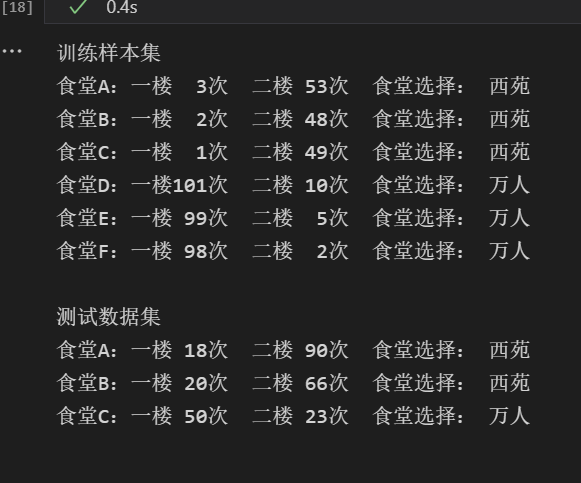
from numpy import *
import operator
 
#训练样本集以及对应的类别
def createDateSet():
    group = array([[3,53],[2,48],[1,49],[101,10],[99,5],[98,2]])
    labels = ['西苑','西苑','西苑','万人','万人','万人']
    return group,labels
 
def classify(inX, dataSet, labels, k):
    #dataSetSize是训练样本集数量
    dataSetSize = dataSet.shape[0]
 
    #距离计算——欧式距离公式
    #tile函数，把inX变成能与dataSet相减的二维数组
    diffMat = tile(inX, (dataSetSize, 1)) - dataSet
    sqDiffMat = diffMat ** 2
    #axis=1是列相加求和，即得到(x1-x2)^2+(y1-y2)^2的值
    sqDistances = sqDiffMat.sum(axis = 1)    
    distances = sqDistances ** 0.5
 
    #按照距离递增次序排序，返回下标
    sortedDistIndicies = distances.argsort()
 
    #选择距离最小的k个点
    classCount = {}
    for i in range(k):
        voteILabel = labels[sortedDistIndicies[i]]
        classCount[voteILabel] = classCount.get(voteILabel,0) + 1
 
    #按照字典里的关键字的值排序，reverse=True降序排序
    sortedClassCount = sorted(classCount.items(), key = operator.itemgetter(1), reverse = True)
   
    #返回类别最多的标签
    return sortedClassCount[0][0]

 

测试算法：

i = 0
print("训练样本集")
group, labels = createDateSet()
for item in group:
    print('食堂%c：一楼%3d次  二楼%3d次  食堂选择： %s'%(chr(ord('A')+i),item[0],item[1],labels[i]))
    i += 1
 
print("\n测试数据集")
myTests = array([[18,90],[20,66],[50,23]])
myLabels = []
for i in range(3):
    myLabels.append(classify(myTests[i], group, labels, 3))
    print('食堂%c：一楼%3d次  二楼%3d次  食堂选择： %s'%(chr(ord('A')+i),myTests[i][0],myTests[i][1],myLabels[i]))

 

测试结果：

9.扩展

补充了解——ANN算法

将KNN扩展至大规模数据的方法是使用 ANN 算法（Approximate Nearest Neighbor），以彻底避开暴力距离计算。ANN 是一种在近邻计算搜索过程中允许少量误差的算法，在大规模数据情况下，可以在短时间内获得卓越的准确性。 

 

人工神经网络（ANN）由一个输入层和一个输出层组成，其中输入层从外部源（数据文件，图像，硬件传感器等）接收数据，一个或多个隐藏层处理数据，输出层提供一个或多个数据点基于网络的功能，根据不同的问题，可以加入多个隐藏层。

 

神经网络的好处和局限性：

1. 优越性：

• 具有自学习功能 。
• 具有联想存储功能 。
• 具有高速寻找优化解的能力。

2. 局限性：

• 神经网络需要大量数据，非常消耗资源，开销也非常大的，而且训练时间长，还需要耗费很大的人力物力。
• 神经网络在概括方面很不好。
• 神经网络是不透明的。