tarjan求割点割边及缩点

割点割边的定义不说了。

定义 dfn 为 dfs 序，low 为该点不经过父亲并只走一次通往 dfs 序比其小的点的情况下能走到的最小的点的 dfs 序。

若 low[v]>=dfn[x] 则说明其儿子在不经过其的情况下无法向上，则该点为割点。

若 low[v]>dfn[x] 且满足不走反向边，说明去掉边后该儿子连其父亲都走不到，该边即为割边。

另外注意一下，当判断根节点是不是割点时，要至少有两个儿子满足条件。

还有，为什么在经过已经走过的点时,low[x]=min(low[x],dfn[v]) ？

就是说回溯的时候不能走到被删掉的点，所以回溯low是会走到不正确的更小的节点，在dfn已经可以判断的情况下就没必要一定要走到最小了。

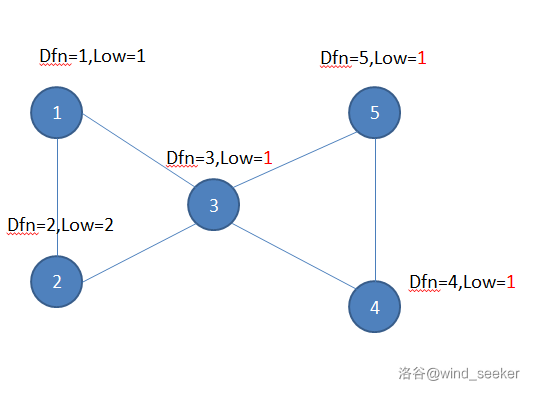
这个图已经很能说明问题了，如果low[x]=min(low[x],low[v]),节点3就不是割点了。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll n,m,dfn[1000000],low[1000000],cnt,pd[1000000];
ll ans1,ans2;
ll head[1000000],tot;
struct nood{
    ll v,nxt;
}es[1000000];
void adde(ll x,ll y){
    es[++tot].v=y,es[tot].nxt=head[x],head[x]=tot;
}
void dfs(ll x){
    ll tj=0;
    dfn[x]=low[x]=++cnt;
    for(int i=head[x];i;i=es[i].nxt){
        ll v=es[i].v;
        if(!dfn[v]){
            dfs(v);
            low[x]=min(low[x],low[v]);
            if(low[v]>=dfn[x]){
                tj++;
            }
        }
        else{
            low[x]=min(low[x],dfn[v]);
        }
    }
    if(x==1&&tj>=2){
        ans1++;
    }
    else if(x!=1&&tj>=1){
        ans1++;
    }
    return;
}

void dfs1(ll x,ll edge){
    dfn[x]=low[x]=++cnt;
    for(int i=head[x];i;i=es[i].nxt){
        ll v=es[i].v;
        if(!dfn[v]){
            dfs1(v,i);
            low[x]=min(low[x],low[v]);
            if(low[v]>dfn[x]){
                if(!pd[i]&&!pd[(i^1)])
                    ans2++;
                pd[i]=pd[(i^1)]=1;
            }
        }
        else if(i!=(edge^1)){
            low[x]=min(low[x],dfn[v]);
        }
    }
    return;
}


int main(){
    tot=1;
    cin>>n>>m;
    ll x,y;
    for(int i=1;i<=m;i++){
        cin>>x>>y;
        adde(x,y);
        adde(y,x);
    }
    dfs(1);
    cout<<ans1<<endl;
    memset(dfn,0,sizeof(dfn));
    memset(low,0,sizeof(low));
    cnt=0;
    dfs1(1,-1);
    cout<<ans2<<endl;
}

缩点

这个讲的好

code:

#include<bits/stdc++.h>
#define ll long long
#define mod 100003
#define ull unsigned long long
#define db double
using namespace std;
ll n,m,a[1000000],head[1000000],tot,dfn[1000000],low[1000000],cnt;
ll st[1000000],he,vis[1000000];
ll k[1000000];
struct nood{
    ll v,nxt;
}es[1000000];
void adde(ll x,ll y){
    es[++tot].v=y,es[tot].nxt=head[x],head[x]=tot;
}
void dfs(ll x){
    dfn[x]=low[x]=++cnt;
    st[++he]=x;
    vis[x]=1;
    for(int i=head[x];i;i=es[i].nxt){
        ll v=es[i].v;
        if(!dfn[v]){
            dfs(v);
            low[x]=min(low[x],low[v]);
        }
        else if(vis[v]){
            low[x]=min(low[x],dfn[v]);
        }
    }
    if(low[x]==dfn[x]){
        while(1){
            k[st[he]]=x;
            vis[st[he]]=0;
            if(st[he]==x){
                he--;
                break;
            }
            a[x]+=a[st[he]];
            he--;
        }
    }
}
int main(){
    cin>>n>>m;
    // for(int i=1;i<=n;i++){
    //     cin>>a[i];
    // }
    ll x,y;
    for(int i=1;i<=m;i++){
        cin>>x>>y;
        adde(x,y);
    }
    for(int i=1;i<=n;i++){
        if(!dfn[i]){
            dfs(i);
        }
    }
    for(int i=1;i<=n;i++){
        cout<<i<<":"<<k[i]<<endl;
    }
}