矩阵快速幂优化前缀和相关的DP

先复习一下矩阵乘法：

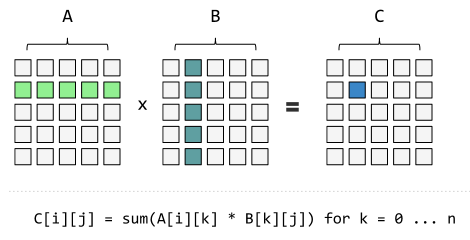
来一个最基础的斐波拉契数列：

\(f_i=f_{i-1}+f_{i-2}\)

求 \(f_n (n<=1e9)\)

显然，这道题用递推做不了一点。

我们在一个很不明显的转换，换成矩阵乘法。

我们构建这样两个矩阵：

\([a_{i-1}, a_{i-2}]\) * \( \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \) = \([a_{i}, a_{i-1}]\)

很神奇的发现，乘一次就可以往后推一个数。

那么，怎么快速处理处理这个乘法呢？

我们可以使用快速幂。

重载乘法后，跟正常的快速幂无异。

伪代码如下：

void po(ll b){
    while(b){
        if(b&1){
			ans=ans*base;
		}
        base=base*base;
        b>>=1;
    }
}

然后就可以完美解决啦。

这个方法适用于很多 \(f_i=f_{i-x}+f_{i-y}+...+f_{i-z}\) 的问题，非常有实力。