CDQ分治总结

CDQ分治总结

这个不能算是一种算法，只能说是一种思想，直接上例题吧。

二维偏序（or 逆序对）

有 $ n $ 个元素，第 $ i $ 个元素有 $ a_i,b_i $ 两个属性，求满足 $ a_j \leq a_i $ 且 $ b_j \leq b_i $ 且 $ j \ne i $ 的 \(j\) 的数量。

$ 1 \leq n \leq 10^5$，$1 \leq a_i, b_i \le k \leq 2 \times 10^5 $。

两种方法都可以解决这个问题。

• 并规排序

首先，把序列按照第一维排序。

然后，对第二维使用并规排序，并在此时统计答案。

简单来说，在我们合并两个序列：\([l,mid],[mid+1,r]\)时，两个序列中的第二维已经整体有序，而且第一个区间里的第一维必然大于第二个区间里的第一维，所以可以使用双指针来统计数量。（当然二分也可以啦）。

• 树状数组

首先，把序列按照第一维排序。

然后，依次把第二维压进树状数组去，每次查询即可。

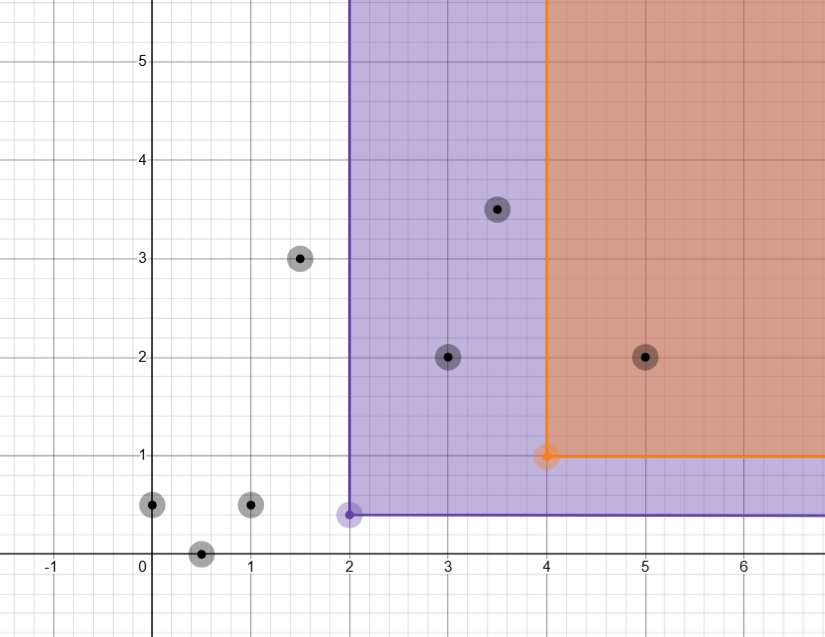
如图，设 \(f[p]\) 为 \(y=p\) 直线上的点，从后往前枚举，加一个压一个，统计即可。（因此我们可以看出，数据的范围大小不能太大，不然数组开不下，需要离散化）。

P3810 【模板】三维偏序

有 $ n $ 个元素，第 $ i $ 个元素有 $ a_i,b_i,c_i $ 三个属性，设 $ f(i) $ 表示满足 $ a_j \leq a_i $ 且 $ b_j \leq b_i $ 且 $ c_j \leq c_i $ 且 $ j \ne i $ 的 \(j\) 的数量。

$ 1 \leq n \leq 10^5$，$1 \leq a_i, b_i, c_i \le k \leq 2 \times 10^5 $。

联系上面两种方法即可。记得去重。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
ll n,k;
ll tr[1000000],cnt,res[1000000];
ll lowbit(ll x){
	return ((x)&(-x));
} 
void update(ll i,ll x){
	for(;i<=k;i+=lowbit(i)){
		tr[i]+=x;
	}
}
ll query(ll i,ll x){
	ll ans=0;
	for(;i;i-=lowbit(i)){
		ans+=tr[i];
	}
	return ans;
}
struct nood{
	ll a,b,c;
	ll sl,ans;
}a[1000000],rep[1000000];
bool cmp(nood x,nood y){
	if(x.a!=y.a){
		return x.a<y.a;
	}
	if(x.b!=y.b){
		return x.b<y.b;
	}
	return x.c<y.c;
}
void cdq(ll l,ll r){
	if(l==r){
		return;
	}
	ll mid=(l+r)>>1;
	ll p=l,q=mid+1,len=0,anss=0;
	cdq(l,mid);cdq(mid+1,r);
	while(p<=mid&&q<=r){
		if(a[p].b<=a[q].b){
			update(a[p].c,a[p].sl);
			rep[++len]=a[p++];
		}
		else{
			a[q].ans+=query(a[q].c,a[q].sl);
			rep[++len]=a[q++];
		}
	}
	//没搞完的
	while(p<=mid){
		update(a[p].c,a[p].sl);
		rep[++len]=a[p++];
	} 
	while(q<=r){
		a[q].ans+=query(a[q].c,a[q].sl);
		rep[++len]=a[q++];
	}
	for(int i=l;i<=mid;i++){
		update(a[i].c,-a[i].sl);
	}
	for(int i=1;i<=len;i++){
		a[l+i-1]=rep[i];//排序 
	}
}
int main(){
	cin>>n>>k;
	for(int i=1;i<=n;i++){
		cin>>a[i].a>>a[i].b>>a[i].c;
		a[i].sl = 1;
        a[i].ans = 0;
	}
	sort(a+1,a+n+1,cmp);
	cnt=1;
	for(int i=2;i<=n;i++){
		if(a[cnt].a==a[i].a&&a[cnt].b==a[i].b&&a[cnt].c==a[i].c){
			a[cnt].sl++;//去重
		}
		else{
			cnt++;
			a[cnt]=a[i];
		}
	}
	cdq(1,cnt);
	for(int i=1;i<=cnt;i++){
		res[a[i].ans+a[i].sl-1]+=a[i].sl;
	}
	for(int i=0;i<n;i++){
		cout<<res[i]<<endl;
	}
} 

顺便讲一下为什么要去重，比如说有3组数，分别是

(0,0,0),(1,1,1),(1,1,1)

理论上来说它们的贡献应该分别为

0 2 1

但是，如果不去重，它们的贡献就会变成：

0 2 2

答案就多了。