hao-gu-shi-zhi-er

好故事之贰

posted on 2023-12-05 14:07:55 | under | source

首先，我们观察数据，发现第一个性质就是输出 0，但是第二个性质似乎有用，我们就从它下手。

如果这些区间两两不包含，一个简单的思路就是先将他们按照 \(l\) 从小到大排序，然后进行处理。

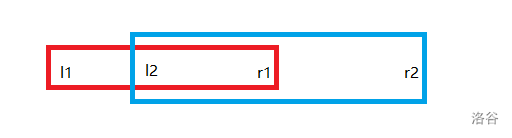
我们发现对于一对确定的 \(i,j(j<i)\)，在排序后它们对答案的贡献可以写作 \(a_i\times a_j\times(r_j-l_i+1)\)，若他们的交集为空这个式子的值为负，对答案无影响。

观察到对于一个固定的 \(i\)，我们只需求出 \(\max\limits_{j=1}^{i-1}\left\{a_jr_j-a_j(l_i-1)\right\}\)。这个东西明显可用李超线段树维护，又由于是全局插入线段，单次插入查询的时间复杂度为 \(O(\log_2n)\)。

但是如果区间之间又相互包含的情况，上式就不成立，我们考虑分开处理。

还是将区间全部按 \(l\) 从小到大排序，我们考虑使用 cdq 分治的思想。

如果区间 \(j\) 不包含区间 \(i(j<i)\)，那么必定满足 \(l_j<l_i\wedge r_j<r_i\)。

我们可以在 cdq 的时候对其进行处理。

在分治时，现在以满足了左段的 \(l\) 都小于右段，我们只需要按 \(r\) 从小到大归并在一起。在归并的时候，如果这是一个左段的点，我们就在李超树中插入它，如果是右段的点就更新答案。

同理，如果区间 \(j\) 包含区间 \(i\)，那么必定满足 \(l_j<l_i\wedge r_j>r_i\)，我们只需要再 cdq 一次，记录下满足条件的 \(j\) 中 \(a_j\) 的最大值即可。

代码：

  #include<bits/stdc++.h>
  #define int long long
  using namespace std;
  char buf[1000005],*p1,*p2;
  #define gc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++)
  int read(){
      int x=0;char c=gc();
      while(c>'9'||c<'0')c=gc();
      while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=gc();
      return x;
  }
  void write(__int128 x){
      if(x>9)write(x/10);
      putchar(x%10+'0');
  }
  int n,tot;
  __int128 ans;
  struct line{
      int k,b;
  }a[1000005];
  int sum;
  int get(int id,int pos){
      return a[id].k*pos+a[id].b;
  }
  struct qqq{
      int l,r,a;
      inline bool operator<(const qqq &t)const{return l<t.l;}
  }x[1000005],b[1000005];
  struct ST{
      int cnt;
      struct Node{
          int son[2],pos;
      }c[20000005];
      int New(){
          cnt++;
          c[cnt].pos=c[cnt].son[0]=c[cnt].son[1]=0;
          return cnt;
      }
      int down(int q,int L,int R,int id){
          if(!q)q=New();
          int mid=L+R>>1;
          if(get(id,mid)>get(c[q].pos,mid))swap(c[q].pos,id);
          if(get(id,L)>get(c[q].pos,L))c[q].son[0]=down(c[q].son[0],L,mid,id);
          if(get(id,R)>get(c[q].pos,R))c[q].son[1]=down(c[q].son[1],mid+1,R,id);
          return q;
      }
      int Add(int q,int L,int R,int l,int r,int id){
          if(!q)q=New();
          if(l<=L&&R<=r){
              q=down(q,L,R,id);
              return q;
          }
          int mid=L+R>>1;
          if(l<=mid)c[q].son[0]=Add(c[q].son[0],L,mid,l,r,id);
          if(mid<r)c[q].son[1]=Add(c[q].son[1],mid+1,R,l,r,id);
          return q;
      }
      int Get(int q,int L,int R,int x){
          if(!q)return 0;
          if(L==R)return get(c[q].pos,x);
          int mid=L+R>>1,res;
          if(x<=mid)res=Get(c[q].son[0],L,mid,x);
          else res=Get(c[q].son[1],mid+1,R,x);
          if(res<get(c[q].pos,x))res=get(c[q].pos,x);
          return res;
      }
  }T;
  void cdq1(int l,int r){//第一次cdq
      if(l==r){
          b[l]=x[l];
          return;
      }
      int mid=l+r>>1;
      cdq1(l,mid);cdq1(mid+1,r);
      int tot=0,p=l,q=mid+1;
      T.cnt=0;
      T.New();
      sum=0;
      while(p<=mid||q<=r){
          if(p<=mid&&(q>r||b[p].r<=b[q].r)){//插入左段点
              x[l+tot]=b[p];
              a[++sum]=line({-b[p].a,b[p].a*b[p].r});
              T.Add(1,0,1e9,0,1e9,sum);
              tot++;p++;
          }
          else{//更新答案
              x[l+tot]=b[q];
              ans=max(ans,(__int128)b[q].a*T.Get(1,0,1e9,b[q].l));
              tot++;q++;
          }
      }
      for(int i=l;i<=r;i++)b[i]=x[i];
  }
  void cdq2(int l,int r){//第二次cdq
      if(l==r){
          b[l]=x[l];
          return;
      }
      int mid=l+r>>1;
      cdq2(l,mid);cdq2(mid+1,r);
      int tot=0,p=l,q=mid+1,maxn=0;
      while(p<=mid||q<=r){
          if(p<=mid&&(q>r||b[p].r>=b[q].r)){
              x[l+tot]=b[p];
              maxn=max(maxn,b[p].a);//记录最大值
              tot++;p++;
          }
          else{
              x[l+tot]=b[q];
              ans=max(ans,(__int128)b[q].a*(b[q].r-b[q].l)*maxn);
              tot++;q++;
          }
      }
      for(int i=l;i<=r;i++)b[i]=x[i];
  }
  signed main()
  {
      n=read();
      for(int i=1;i<=n;i++)x[i].l=read()-1,x[i].r=read(),x[i].a=read();
      sort(x+1,x+n+1);
      cdq1(1,n);
      sort(x+1,x+n+1);
      cdq2(1,n);
      write(ans);
      return 0;
  }