gai-shuai-1-post

概率1

posted on 2022-08-15 13:31:44 | under 总结 | source

主要是古典概率。

https://vjudge.net/contest/510563#overview

A

题目很简单，给定两个数 \(a,b\) ，求在 1 到 6 以内大于等于 \(a\) 和 \(b\) 的数的占比。

B

你有 \(n\) 张卡牌，第 \(i\) 张上有一个红色是数字 \(R_i\) 和一个蓝色的数字 \(B_i\)，求将这些卡牌排列后，是红色数字大于蓝色数字的概率大还是蓝色数字大于红色数字的概率大，或者相等。

显然，如果 \(R_i=B_i\)，那么这张卡牌就是废的，因为不管怎么排列，都不会有什么影响。如果 \(R_i>B_i\) 那当我们把这张卡牌排在前面时，红色就更优，反之亦然。

所以最后的判断依据就是比较 \(R_i>B_i\) 的卡牌数量与 \(R_i<B_i\) 的卡牌数量的大小关系。

C

有 \(n\) 个门，你要选择一个，然后 NPC 会帮你打开 \(n-2\) 个，这 \(n-2\) 个门后都没有奖品，问你选择你选择的那一个门与选择另一个门得到奖品的概率分别是多少。

显然，在最开始每个门的概率都是 \(\dfrac{1}{n}\)，那么我们选的门的概率就是 \(\dfrac{1}{n}\)，那么，另一个门的概率就是 \(1-\dfrac{1}{n}=\dfrac{n-1}{n}\) 了。

D

你需要按照一个字符串行走，但你收到了另一个字符串，问你依然在最后走到正确的地方的概率。

看看数据范围，10。显然暴搜，最后对于所有的情况算到达的情况的占比。

E

两个弓箭手 A 和 B，命中的概率分别是 \(\dfrac{a}{b}\) 和 \(\dfrac{c}{d}\)，A 先射。谁先射中对方就赢，问 A 赢的概率。

由于对精度的要求比较小，我们可以枚举在第几回合 A 获胜。对于第 \(i\) 回合，想要进行的这里，要求前 \(i-1\) 个回合两人全部射空，概率为 \((1-\dfrac{a}{b})^{i-1}\times(1-\dfrac{c}{d})^{i-1}\)。然后 A 命中了，概率为 \(\dfrac{a}{b}\)。所以乘起来就是 \((1-\dfrac{a}{b})^{i-1}\times(1-\dfrac{c}{d})^{i-1}\times\dfrac{a}{b}\)。然后对于 \(\forall i\in[1,1000000]\) 算出来累加就行了（到 1000000 的原因是到怎么大过后算出来的结果远小于 \(10^{-6}\) 了，不会有什么影响）。

F

问一个一元二次方程 \(x^2+\sqrt{p}+q=0,p\in[0,a],q\in[-b,b]\) 有实数根的概率。

• 当 \(b=0\) 时，显然概率是 1。

• 当 \(a=0\) 时，概率为 0.5（因为只有当 \(0\le b\) 时才行）。

• 否则就是看 \(4q\le p\) 的概率。

而我们可以将所有情况看成一个矩形，概率就是矩形与 \(4q\le q\) 这个半平面的交的面积除以整个矩形的面积。那么，怎么求这个交的面积呢？ 当然是半平面交。 其实我们发现就只有一条直线，所以可以直接分类讨论。

如果是下图这种情况，即当 \(b\le\dfrac{a}{4}\) 时，我们需要求一个梯形的面积，结合题目，我们知道上底为 \(b\)，下底为 \(b+\dfrac{a}{4}\)，高为 \(a\)，所有面积 \(S=\dfrac{[b+(b+\dfrac{a}{4})]\times a}{2}\)。

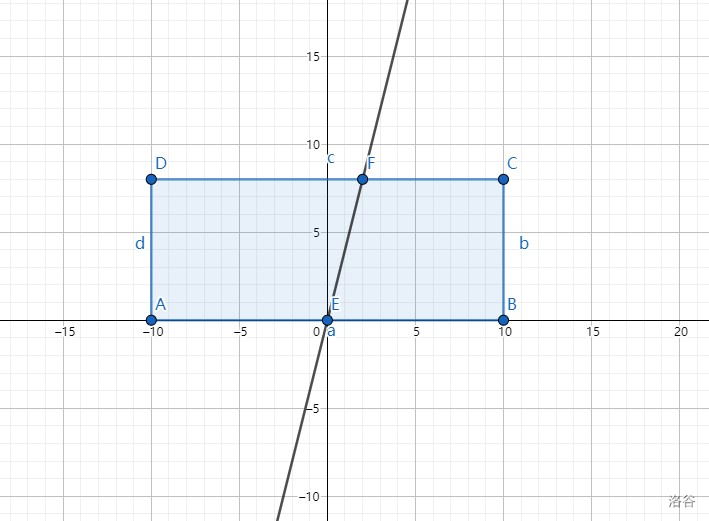
对于另一种情况，即当 \(b>\dfrac{a}{4}\) 时,我们考虑割补，易求出 \(S=2ab-\dfrac{b\times 4b}{2}\)。

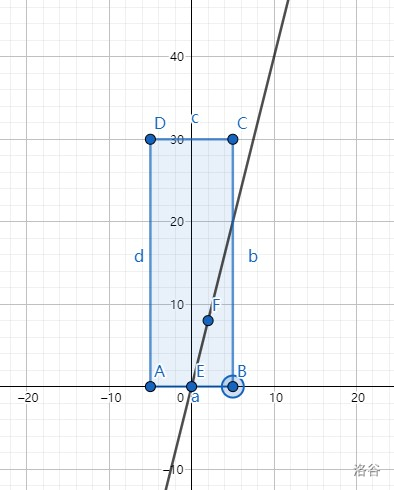
G

你有 \(m\) 副相同牌，每一副有 \(n\) 张带有不同数值的牌，从所有牌里面选出来 \(n\) 张，再在这 \(n\) 张牌先后里面选两张（可以是同一张），求这两张牌上的数值是相同的的概率。

首先，我们考虑两次选的是同一张牌，概率为 \(\dfrac{1}{n}\)。这是因为，当我们先选了一张牌之后就必须再选它。

然后，我们考虑第二次选的牌不是原来的那一张，但是只与其相同。不是同一张的概率为 \(\dfrac{n-1}{n}\)，这很明显。然后在剩下的 \(nm-1\) 张牌中，有 \(m-1\) 张牌的数值与第一次选的牌相同，选中的概率为 \(\dfrac{m-1}{n\cdot m-1}\)。所以这种情况的概率为 \(\dfrac{n-1}{n}\times \dfrac{m-1}{n\cdot m-1}\)。

最后，我们把两种情况的概率加起来就行了。

注意：当 \(n=m=1\) 时需要特判，这时的答案为 1。

H

一把左轮手枪，我们知道弹仓内子弹的相对位置。你在和你的朋友玩俄罗斯转盘 （这什么垃圾朋友）。你的朋友先将弹仓随机转了任意下，然后开枪了，他没有挂。现在该你了，你需要决定是直接开枪还是转随机下再开枪。没转一次或开一枪现在的子弹槽会向移到它左边相邻的子弹槽的位置上。

如果你选择直接开枪，那么活下来的概率就是一个没有子弹的位置后面一个也没有子弹的位置的位置在所有没有子弹的位置中的占比。

如果你选择旋转，那么活下来的概率就是没有子弹的位置在所有位置中的占比。

最后判断怎么的操作活下来的概率大就行了。

I

有 \(n\) 个人，题他们要去买东西，每个人买东西的概率为 \(p_i\)，已知刚好有 \(r\) 个人买了东西，求每个人买东西的概率。

我们都知道条件概率的式子是 \(P(A|B)=\dfrac{P(AB)}{P(B)}\)。

那么我们设 \(B\) 代表刚好有 \(r\) 个人买了东西，\(A_i\) 表示第 \(i\) 个人买了东西。那么我们就是要求 \(P(A_i|B),i=\overline{1,2,\cdots,n}\)。由于 \(n\) 只有 20，所以我们可以 dfs 枚举出哪些人要买东西然后累加这些概率。