去**的线性代数
\(\ksi\)
粘一段 oi-wiki 上对线代的描述:
线性代数源于人们的观察。人们发现,很多对象都拥有相似的性质,比如:
-
力可以被分解、合成。
-
对于任意的 \(k,x_0,k \sin (x-x_0)\) 可以分解成 \(k_1\sin x + k_2\cos x\)。
这些性质与所描述对象的 缩放、分解、叠加 等有关。线性代数把这些性质从具体对象中抽象出来,作为一个独立的学科来研究。
由此可见,线代是一个历史悠久,用处很大的数学分支。
这里略过一些线代中的基础定义。
先从线代最初的作用:解方程说起。假设我们有如下的一个方程组:
如果我们用矩阵和向量来描述方程组中的参数和未知数,可以得到:
\(A\times \vec x=\vec b\),其中 \(\vec x\) 和 \(\vec b\) 是两个列向量,分别存储了所有的 \(x\) 和 \(b\)。
考虑只记录 \(A\) 和 \(\vec b\),我们考虑平时消元的过程:依次处理所有的未知数 \(x_i\),找到一个含有 \(x_i\) 的方程,将这个方程的若干倍加到其他的方程上从而消去其他方程中的 \(x_i\) 项,直到所有方程都呈现 \(ax=b\) 的形式。我们称其为 高斯-约旦消元(如果每次只消去后面的方程中的 \(x_i\),解出一个 \(x\) 后再依次回代的叫高斯消元)。
其中将方程的若干倍加到其他方程上的一步是整个算法变化最多的一步:
- 如果方程组在实数域内就直接用实数除法。
- 如果方程组定义在模质数意义下就用逆元。
- 如果方程组定义在模任意自然数意义下考虑对于两个方程辗转相除,将某一个方程的这一项消到 0。
- 如果方程定义在模 2 意义下考虑用 bitset 优化此过程。
一般情况下复杂度为 \(O(n^3)\)。处理特殊矩阵时会有更优秀的复杂度。
我们都知道如果一组向量无法相互表示那它们就是线性无关的,而一组向量的极大线性无关子集就成为这组向量的线性基。
考虑如何求解线性基,每次插入一个向量时从它的最高位开始考虑,如果现在它的最高位 \(p\) 没有对应的向量 \(b_p\),就将其插入,否则用 \(b_p\) 将给向量的 \(p\) 位置给消去。当向量被消为 0 时就表明现在线性基中的向量可以表示该向量,无法插入。
我们称一个向量组的线性基的大小为该向量组的秩,或是维数。
对于一个矩阵,如果我们将其看为将若干个行向量堆叠在一起,这这些行向量的秩称为矩阵的行秩。同样的定义有矩阵的列秩。同时我们有对于任意矩阵,行秩等于列秩,证明略。
行秩和列秩统称为矩阵的秩,记为 \(\operatorname{rank} A\)。
对于一个方阵 \(A_{n,n}\),定义方阵的行列式 \(\det A=\sum\limits_{p_{1,n}}(-1)^{\sigma(p)}\prod\limits_{i=1}^nA_{i,p_i}\),其中 \(\sigma(p)\) 表示排列 \(p\) 的逆序对数。
或者行列式还可以由 Laplace 展开式计算: \(\det A=\sum_{i=1}^n(-1)^{1+i}A_{1,i}\times \det M_{1,i}\),其中 \(M_{i,j}\) 表示原方阵 \(A\) 中删去第 \(i\) 行和第 \(j\) 列后剩余的子矩阵,称为余子阵,\(\det M_{i,j}\) 被称为余子式。
这告诉我们一个三角矩阵的行列式值等于其对角线上所有元素的乘积。
矩阵的行列式有如下几条重要的性质:
- 如果将矩阵 \(A\) 的某一行或某一列整体乘上一个常数 \(c\),则 \(\det A'=c\cdot\det A\)。
- 如果矩阵 \(A\) 和矩阵 \(B,C\) 满足 \(A\) 的某一行或某一列是 \(B\) 和 \(C\) 对应的行或列的和,矩阵中的其他位置分别相等,则有 \(\det A=\det B+\det C\)。
- 交换矩阵 \(A\) 的某两行或某两列的位置,矩阵的行列式值取反。
结合之前的三角矩阵行列式值,我们可以回想高斯消元的过程,发现消元的结果就是一个三角矩阵,也就是我们可以在 \(O(n^3)\) 的复杂度内求出行列式的值。
同时,如果一个矩阵的行列式值不为 0,一个充要条件是该矩阵满秩。证明显然。
Cauchy-binet formula,柯西比内公式的内容如下:对于两个矩阵 \(U_{n\times m}\) 和 \(V_{m\times n}\),其乘积的行列式 \(\det (U\times V)=\sum\limits_{S=\binom{[m]}n}\det U_{[n],S}\times \det V_{S,[n]}\)。表示对于 1 到 \(m\) 中每一个大小为 \(n\) 的子集,然后将 \(U,V\) 中对应的 \(n\) 阶子矩阵的行列式的乘积求和。
显然如果 \(n>m\) 积的行列式为 0(因为两矩阵乘积的秩不超过这两个矩阵的秩,所有乘积矩阵明显不是满秩的)。
该公式可以算一些神秘的组合意义题。鬼知道能不能用上。
Matrix Determinant Lemma,矩阵行列式引理表示为:
证明如下:
考虑块矩阵乘法,\(\begin{pmatrix}I_n&\\V&I_m\end{pmatrix}\begin{pmatrix}I_n+UV&U\\&I_m\end{pmatrix}\begin{pmatrix}I_n&\\-V&I_m\end{pmatrix}=\begin{pmatrix}I_n&U\\&I_m+VU\end{pmatrix}\)
由于上式所有矩阵都是三角矩阵,因此有 \(1\times|I_n+UV|\times1=|I_m+VU|\)。
另外此引理还有推广形式:对于一个 \(n\) 阶可逆方阵 \(A\),有 \(|A+UV|=|A|\cdot|I_n+(A^{-1}U)V|=|A|\cdot|I_m+VA^{-1}U|\)。
LGV 引理,可以用来处理有向无环图上不相交路径计数等问题。
在 DAG 上,我们选取一个起点集合 \(A_{1,n}\) 和一个终点集合 \(B_{1,n}\)。记 \(w(u,v)\) 为对于从 \(u\) 到 \(v\) 的每一条路径,路径经过的边的边权的积的和。
则矩阵 \(\begin{vmatrix}&w(A_1,B_1) ,&\cdots,&w(A_1,B_n)\\&\vdots&\ddots&\vdots\\&w(A_n,B_1),&\cdots,&w(A_n,B_n)\end{vmatrix}\) 的行列式表示 \(\sum\limits_{S:A\to B}(-1)^{t(\sigma(S))}\prod\limits_{i=1}^n w(S_i)\)。
其中 \(S_i\) 是从 \(A_i\) 到 \(B_{\sigma_i}\) 的路径,\(t(\sigma)\) 是这个排列的逆序对数。且对于任意 \(i\neq j\),\(S_i\) 和 \(S_j\) 无公共点,感性理解就是如果两条路径有公共点,例如下图
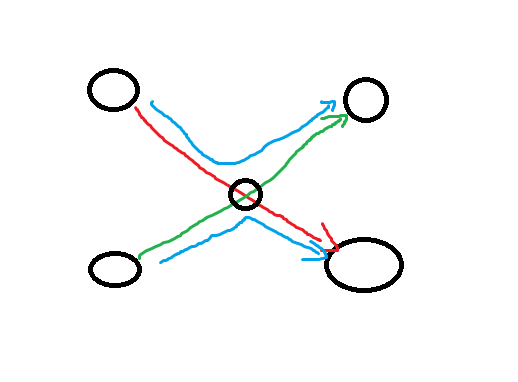
绿色路径和红色路径在中间有交点,但当统计蓝色路径是会被容斥掉。
Schwartz–Zippel 引理
对于域 \(F\) 中一个 \(m\) 元 \(n\) 次多项式 \(f(x_1,x_2,\cdots,x_m)\),对每个 \(x\) 随机取 \(F\) 中的值,\(f=0\) 的概率为 \(\dfrac n{|F|}\)。
证明显然。
矩阵树定理
对于一个无向连通图 \(G(V,E)\),我们记矩阵 \(D(G)\) 为度数矩阵,满足 \(D_{i,i}=\deg i,D_{i,j}=0(i\neq j)\)。另记矩阵 \(A(G)\) 为邻接矩阵,\(A_{i,j}\) 表示 \(i,j\) 间有多少条可区分的边,则其 Laplace 矩阵 \(L(G)=D(G)-A(G)\)。则图 \(G\) 的生成树数量为其 Laplace 矩阵 \(L(G)\) 的任意 \(n-1\) 阶主子式的值。
证明:考虑生成树的生成,我们先随便删去一个点,然后要求其余点都选一条出边且所有选出的边不成环。则总方案数为 \(\sum\limits_{k=0}(-1)^k\texttt{选择k个环}\times\prod\limits_{\texttt{x不属于环}}d_x\)。考虑矩阵树定理的内容,将行列式枚举的排列表示为置换环后,每一个自环代表不属于环上的点,方案数为 \(d_i\);而一个长为 \(len\) 的环带来的逆序对为 \(len-1\) 个,带来的 \(-1\) 是 \(len\) 个,总贡献是 \(2len-1\),也就是一个环会为最终的累和带来一个 \(-1\),满足前面容斥的表达。
对于有向图,定义 \(D_{in}(A)\) 和 \(D_{out}(A)\) 表示入度矩阵和出度矩阵,则其内向生成树个数为 \(D_{out}-A\) 的任意 \(n-1\) 阶主子式,外向生成树个数为 \(D_{in}-A\) 的任意 \(n-1\) 阶主子式。证明略。
讲课内容就这些了,但是题目有一堆,并且还个个身怀绝技。
神奇的矩阵
Yet Another Linear Algebra Problem
及其简单,一个是随机化,一个是柯西比内的简单应用。
板的 lgv,也可以用柯西比内做。
省流:lgv,但是不知道终点。
考虑建出网格图,记\((i,j)\) 代表 \(i\) 时刻在 \(j\) 位置,发现从 \((x_1,y_1)\) 走到 \((x_2,y_2)\) 的方案数为 \(\binom{x_2-x_1}{y_2-y_1}\)。同时注意到网格图上要求路径无交等价于起点依次走向终点,所以 LGV 引理不需要担心带符号和的问题,因为就只有一个排列符合要求。
但是发现我们只知道每个机器人的起点二不知道终点,考虑 dp。
设 \(dp_{S,j}\) 表示集合 \(S\) 中所有机器人的终点都确认在 \((n,j)\) 之前的方案数,则有 \(dp_{S,j}=dp_{S,j-1}+\sum\limits_{x\in S}dp_{S\backslash\{x\},j-1}\times(-1)^{Sup(S,x)}\times w(x,j))\)。其中 \(Sup(S,x)\) 表示集合 \(S\) 中比 \(x\) 大的元素的个数(算逆序对),\(w(x,j)\) 表示机器人 \(x\) 走到 \((n,j)\) 的方案数。
最终的答案就是 \(dp_{U,n+maxp}\)。
发现要求所有路径不相交,自然想到 lgv 引理。
考虑先 \(O(k(n+m))\) 求出 \(k+1\) 到 \(n\) 所有位置对应的向量,记点 \(i\) 对应的向量为 \(v_i\),我们本质是求每一个区间 \([l,r]\) 中所有向量的线性基大小。
暴力求解显然是行不通的。
考虑对线性基内的每一个向量记录其插入的时间,如果现在插入的向量 \(v_n\) 的时间晚于这个位置的向量 \(v_p\),我们就将这 \(v_n\) 放在此处,将消去最高项的 \(v_p\) 继续插入。这样做之后,我们考虑刚插入第 \(i\) 给向量后的线性基,每一个存在与线性基中的时间 \(t_i\) 都表明以当前 \(i\) 作为右端点,\(t_i\) 及其之前的左端点会多存在一个向量。所以每次插完一个向量就把所有 \(k\) 个时间拿出来更新答案就可以了。
总复杂度 \(O(k(n+m)+nk^2)\)。
美妙的题。
我们随便找一个矩阵看看,比如说 \(n=6,C=10\) 的:

考虑先把对角线一下的 \(C\) 全部消去,得到:

记 \(v=\dfrac C{1-C}\),这时特判掉 \(C=1\) 的矩阵。得到:

设 \(f_i\) 表示 \([n-i+1,n]\times[n-i+1,n]\) 范围内子矩阵的行列式,\(g_{i,j}\) 表示大小为 \(i\) 的子矩阵把第 \(i\) 行换成第 \(j\) 行后的行列式。
有:\(f_i=f_{i-1}+g_{i-1,i},g_{i,j}=c(i-1,k)\times f_{i-1}+g_{i-1,k}(i\ge3)\)。其中 \(c(i,j)=v\times([i|j]-[(i+1)|j])\)。
设 \(f\) 的差分数组为 \(df\),有 \(df_n=v\times\sum\limits_{i|n\wedge i\neq n}df_i,df_1=\dfrac 1C\)。
写成 DGF 就是 \((1+v)\hat{df}=v\times(\hat{df}\times\zeta)+\dfrac 1C\)。
变形得:\((1+v-v\zeta)\hat{df}=\dfrac 1C\)。
\(1+v-v\zeta\) 对应的数列是:\(1,-v,-v,\cdots\)。
考虑直接杜教筛。
题目要求边不能同时经过多次,考虑将边看作点然后连边,问题就变成了点不相交。
因为要求路径不相交,所以考虑 lgv 引理。但是 lgv 引理求的是行列式,这里显然是积和式更能代表答案,因为行列式为 0 的时候积和式可能不为 0,考虑对每条建出的边随机赋权,然后信仰跑,大概率是不会错的。
回到原题,我们发现另一个问题,如果一个点的度数太大会使新图的边数爆炸,我们结合答案对 \(k\) 取 \(\min\) 的限制考虑如果一个点的度数超过了 \(k\) 就建 \(k\) 个虚点来与所有的边连边,这样总边数就被控制在 \(km\) 只内。记点 \(i\) 的度数和 \(k\) 取模的值为 \(num_i\)。
现在对于一个点 \(x\),我们可以得到一个 \(num_1\times num_x\) 的矩阵 \(A_i\),lgv 引理的过程就是找一个最大的子矩阵使得行列式不为 0,然后我们发现这其实就是矩阵的秩,高消跑完看剩了几行就可以了。
总复杂度 \(O(k(nk+m)km+nk^3)\)

 讲了线代,有感而发,遂有此文。
讲了线代,有感而发,遂有此文。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号