L3HCTF-Cry+Misc部分题目
L3HCTF2025
Crypto
math_problem
import gmpy2
from gmpy2 import *
from Crypto.Util.number import *
from random import randint
from gmpy2 import invert
from scret import flag
def myfunction(num):
output = 0
output=num**3
return output
if __name__ == '__main__':
flag_len = len(flag)
p, q = getPrime(512), getPrime(512)
while True:
r = getPrime(512)
R = bytes_to_long(str(r).encode())
if isPrime(R):
break
n = p * q * r
hint1 = R * r
mod = myfunction(n)
hint2 = pow(3*n+1, p % (2 ** 400), mod)
m = bytes_to_long(flag)
c = pow(m, 65537, n)
print('All data:')
print(f'n = {n}')
print(f'c = {c}')
print(f'hint1 = {hint1}')
print(f'hint2 = {hint2}')
'''
All data:
n = 1031361339208727791691298627543660626410606240120564103678654539403400080866317968868129842196968695881908504164493307869679126969820723174066217814377008485456923379924853652121682069359767219423414060835725846413022799109637665041081215491777412523849107017649039242068964400703052356256244423474207673552341406331476528847104738461329766566162770505123490007005634713729116037657261941371410447717090137275138353217951485412890440960756321099770208574858093921
c = 102236458296005878146044806702966879940747405722298512433320216536239393890381990624291341014929382445849345903174490221598574856359809965659167404530660264493014761156245994411400111564065685663103513911577275735398329066710295262831185375333970116921093419001584290401132157702732101670324984662104398372071827999099732380917953008348751083912048254277463410132465011554297806390512318512896160903564287060978724650580695287391837481366347198300815022619675984
hint1 = 41699797470148528118065605288197366862071963783170462567646805693192170424753713903885385414542846725515351517470807154959539734665451498128021839987009088359453952505767502787767811244460427708303466073939179073677508236152266192609771866449943129677399293427414429298810647511172104050713783858789512441818844085646242722591714271359623474775510189704720357600842458800685062043578453094042903696357669390327924676743287819794284636630926065882392099206000580093201362555407712118431477329843371699667742798025599077898845333
hint2 = 10565371682545827068628214330168936678432017129758459192768614958768416450293677581352009816968059122180962364167183380897064080110800683719854438826424680653506645748730410281261164772551926020079613841220031841169753076600288062149920421974462095373140575810644453412962829711044354434460214948130078789634468559296648856777594230611436313326135647906667484971720387096683685835063221395189609633921668472719627163647225857737284122295085955645299384331967103814148801560724293703790396208078532008033853743619829338796313296528242521122038216263850878753284443416054923259279068894310509509537975210875344702115518307484576582043341455081343814378133782821979252975223992920160189207341869819491668768770230707076868854748648405256689895041414944466320313193195829115278252603228975429163616907186455903997049788262936239949070310119041141829846270634673190618136793047062531806082102640644325030011059428082270352824026797462398349982925951981419189268790800571889709446027925165953065407940787203142846496246938799390975110032101769845148364390897424165932568423505644878118670783346937251004620653142783361686327652304482423795489977844150385264586056799848907
'''
首先通过r=gcd(n,hint1)可以恢复r
myfunction(num)函数其实就是进行三次方的操作
hint2 = pow(3*n+1, p % (2 ** 400), mod)可以通过二项式定理恢复p的低400位
再结合copper恢复p,即可分解n
exp:
import gmpy2
from Crypto.Util.number import long_to_bytes
from sage.all import *
n = 1031361339208727791691298627543660626410606240120564103678654539403400080866317968868129842196968695881908504164493307869679126969820723174066217814377008485456923379924853652121682069359767219423414060835725846413022799109637665041081215491777412523849107017649039242068964400703052356256244423474207673552341406331476528847104738461329766566162770505123490007005634713729116037657261941371410447717090137275138353217951485412890440960756321099770208574858093921
c = 102236458296005878146044806702966879940747405722298512433320216536239393890381990624291341014929382445849345903174490221598574856359809965659167404530660264493014761156245994411400111564065685663103513911577275735398329066710295262831185375333970116921093419001584290401132157702732101670324984662104398372071827999099732380917953008348751083912048254277463410132465011554297806390512318512896160903564287060978724650580695287391837481366347198300815022619675984
hint1 = 41699797470148528118065605288197366862071963783170462567646805693192170424753713903885385414542846725515351517470807154959539734665451498128021839987009088359453952505767502787767811244460427708303466073939179073677508236152266192609771866449943129677399293427414429298810647511172104050713783858789512441818844085646242722591714271359623474775510189704720357600842458800685062043578453094042903696357669390327924676743287819794284636630926065882392099206000580093201362555407712118431477329843371699667742798025599077898845333
hint2 = 10565371682545827068628214330168936678432017129758459192768614958768416450293677581352009816968059122180962364167183380897064080110800683719854438826424680653506645748730410281261164772551926020079613841220031841169753076600288062149920421974462095373140575810644453412962829711044354434460214948130078789634468559296648856777594230611436313326135647906667484971720387096683685835063221395189609633921668472719627163647225857737284122295085955645299384331967103814148801560724293703790396208078532008033853743619829338796313296528242521122038216263850878753284443416054923259279068894310509509537975210875344702115518307484576582043341455081343814378133782821979252975223992920160189207341869819491668768770230707076868854748648405256689895041414944466320313193195829115278252603228975429163616907186455903997049788262936239949070310119041141829846270634673190618136793047062531806082102640644325030011059428082270352824026797462398349982925951981419189268790800571889709446027925165953065407940787203142846496246938799390975110032101769845148364390897424165932568423505644878118670783346937251004620653142783361686327652304482423795489977844150385264586056799848907
r = gcd(n, hint1)
print(f"r = {r}")
N1 = n // r
A = (hint2%(n**2) - 1) // n % n
inv3 = inverse_mod(3, n)
k_mod = (A * inv3) % n
p_mod = Integer(k_mod) % (2**400)
print(f"p mod 2^400 = {(p_mod)}")
PR.<x> = PolynomialRing(Zmod(N1), 'x')
f = k_mod + x*(2**400)
roots = f.monic().small_roots(X=2**112, beta=0.49)
x0 = roots[0]
p = Integer(p_mod + x0*(2**400))
q = N1 // p
print(f"p = {p}")
print(f"q = {q}")
phi = (p-1)*(q-1)*(r-1)
d = inverse_mod(65537, phi)
m = pow(c, d, n)
flag = long_to_bytes(m)
print(f"FLAG = {flag}")
EzECDSA
import hashlib
import random
from ecdsa import NIST256p, SigningKey
class FlawedNonceGenerator:
def __init__(self, n):
self.n = n
self.a = random.randrange(1, n)
self.b = random.randrange(1, n)
self.c = random.randrange(1, n)
self.last_k = random.randrange(1, n)
def generate_nonce(self):
current_k = self.last_k
next_k = (self.a * current_k**2 + self.b * current_k + self.c) % self.n
self.last_k = next_k
return current_k
curve = NIST256p
n = curve.order
private_key = SigningKey.from_secret_exponent(random.randrange(1, n), curve=curve)
d = private_key.privkey.secret_multiplier
public_key = private_key.get_verifying_key()
messages = [
b"Hello player, welcome to L3HCTF 2025!",
b"This is a crypto challenge, as you can probably tell.",
b"It's about ECDSA, a very... robust algorithm.",
b"I'm sure there are no implementation flaws whatsoever.",
b"Anyway, here are your signatures. Good luck!",
f"Oh, and the flag is L3HCTF{{{d}}}. Don't tell anyone!".encode(),
]
nonce_generator = FlawedNonceGenerator(n)
f = open('signatures.txt', 'w')
for i in range(6):
k = nonce_generator.generate_nonce()
message = messages[i]
h = int.from_bytes(hashlib.sha256(message).digest(), 'big')
R = k * curve.generator
r = R.x() % n
s_inv = pow(k, -1, n)
s = (s_inv * (h + d * r)) % n
f.write(f"h: {h}, r: {r}, s: {s}\n")
"""
h: 5832921593739954772384341732387581797486339670895875430934592373351528180781, r: 78576287416983546819312440403592484606132915965726128924031253623117138586396, s: 108582979377193966287732302562639670357586761346333866965382465209612237330851
h: 85517239535736342992982496475440962888226294744294285419613128065975843025446, r: 60425040031360920373082268221766168683222476464343035165195057634060216692194, s: 27924509924269609509672965613674355269361001011362007412205784446375567959036
h: 90905761421138489726836357279787648991884324454425734512085180879013704399530, r: 75779605492148881737630918749717271960050893072832415117470852442721700807111, s: 72740499400319841565890543635298470075267336863033867770902108413176557795256
h: 103266614372002123398101167242562044737358751274736728792365384600377408313142, r: 89519601474973769723244654516140957004170211982048028366151899055366457476708, s: 23639647021855356876198750083669161995553646511611903128486429649329358343588
h: 9903460667647154866199928325987868915846235162578615698288214703794150057571, r: 17829304522948160053211214227664982869100868125268116260967204562276608388692, s: 74400189461172040580877095515356365992183768921088660926738652857846750009205
h: 54539896686295066164943194401294833445622227965487949234393615233511802974126, r: 66428683990399093855578572760918582937085121375887639383221629490465838706027, s: 25418035697368269779911580792368595733749376383350120613502399678197333473802
"""
- 签名关系:ECDSA签名满足 \(s_i \cdot k_i \equiv h_i + d \cdot r_i \mod n\),可解出 \(k_i = (h_i + d \cdot r_i) \cdot s_i^{-1} \mod n\)。
- nonce递归:连续的\(k_i\)满足递归关系,如:
- \(k_1 = a \cdot k_0^2 + b \cdot k_0 + c \mod n\)
- \(k_2 = a \cdot k_1^2 + b \cdot k_1 + c \mod n\)
- ...
- 建立方程:将\(k_i\)表示为\(d\)的线性函数:\(k_i = A_i + B_i \cdot d\),其中 \(A_i = h_i \cdot s_i^{-1} \mod n\),\(B_i = r_i \cdot s_i^{-1} \mod n\)。代入递归关系,得到关于\(d\)的方程。
- 多项式求解:利用前5个签名构建一个关于\(d\)的4次多项式方程(模\(n\)),并求解其根。
- 验证候选:对每个候选\(d\),用递归关系预测\(k_5\),并与从第6个签名计算的\(k_5\)比较,验证正确性。
exp:
from sage.all import *
# Given signatures
signatures = [
(5832921593739954772384341732387581797486339670895875430934592373351528180781, 78576287416983546819312440403592484606132915965726128924031253623117138586396, 108582979377193966287732302562639670357586761346333866965382465209612237330851),
(85517239535736342992982496475440962888226294744294285419613128065975843025446, 60425040031360920373082268221766168683222476464343035165195057634060216692194, 27924509924269609509672965613674355269361001011362007412205784446375567959036),
(90905761421138489726836357279787648991884324454425734512085180879013704399530, 75779605492148881737630918749717271960050893072832415117470852442721700807111, 72740499400319841565890543635298470075267336863033867770902108413176557795256),
(103266614372002123398101167242562044737358751274736728792365384600377408313142, 89519601474973769723244654516140957004170211982048028366151899055366457476708, 23639647021855356876198750083669161995553646511611903128486429649329358343588),
(9903460667647154866199928325987868915846235162578615698288214703794150057571, 17829304522948160053211214227664982869100868125268116260967204562276608388692, 74400189461172040580877095515356365992183768921088660926738652857846750009205),
(54539896686295066164943194401294833445622227965487949234393615233511802974126, 66428683990399093855578572760918582937085121375887639383221629490465838706027, 25418035697368269779911580792368595733749376383350120613502399678197333473802)
]
# NIST P-256 curve order
n = 115792089210356248762697446949407573529996955224135760342422259061068512044369
F = GF(n) # Finite field of order n
R.<d> = PolynomialRing(F) # Polynomial ring in d
# Extract the first five signatures for building the equation
h0, r0, s0 = signatures[0]
h1, r1, s1 = signatures[1]
h2, r2, s2 = signatures[2]
h3, r3, s3 = signatures[3]
h4, r4, s4 = signatures[4]
h5, r5, s5 = signatures[5] # For verification
# Compute A_i and B_i for k_i = A_i + B_i * d
A0 = F(h0) * F(s0)**-1
B0 = F(r0) * F(s0)**-1
A1 = F(h1) * F(s1)**-1
B1 = F(r1) * F(s1)**-1
A2 = F(h2) * F(s2)**-1
B2 = F(r2) * F(s2)**-1
A3 = F(h3) * F(s3)**-1
B3 = F(r3) * F(s3)**-1
A4 = F(h4) * F(s4)**-1
B4 = F(r4) * F(s4)**-1
# Define k_i as linear polynomials in d
k0 = A0 + B0 * d
k1 = A1 + B1 * d
k2 = A2 + B2 * d
k3 = A3 + B3 * d
k4 = A4 + B4 * d
# Differences needed for the equation
diff01 = k1 - k0
diff12 = k2 - k1
diff23 = k3 - k2
diff02 = k2 - k0
diff13 = k3 - k1
# Construct the polynomial equation from the recurrence relations
left_part = ((k3 - k2) * diff01 - (k2 - k1) * diff12) * diff23 * diff13
right_part = ((k4 - k3) * diff12 - (k3 - k2) * diff23) * diff01 * diff02
poly = left_part - right_part
# Find roots of the polynomial
roots = poly.roots(multiplicities=False)
# Check each candidate d
found_d = None
for d0 in roots:
d0 = F(d0)
# Evaluate k0 to k4 at candidate d0
k0_val = A0 + B0 * d0
k1_val = A1 + B1 * d0
k2_val = A2 + B2 * d0
k3_val = A3 + B3 * d0
k4_val = A4 + B4 * d0
# Skip if differences are zero (to avoid division by zero)
if k0_val == k1_val or k1_val == k2_val or k2_val == k0_val:
continue
# Compute a from the recurrence relation
term1 = (k3_val - k2_val) * (k2_val - k1_val)**-1
term2 = (k2_val - k1_val) * (k1_val - k0_val)**-1
a_val = (term1 - term2) * (k2_val - k0_val)**-1
# Compute b
b_val = (k2_val - k1_val) * (k1_val - k0_val)**-1 - a_val * (k1_val + k0_val)
# Compute c
c_val = k1_val - a_val * k0_val**2 - b_val * k0_val
# Predict k5 using the recurrence
k5_pred = a_val * k4_val**2 + b_val * k4_val + c_val
# Compute k5 from the sixth signature
k5_ecdsa = (F(h5) + d0 * F(r5)) * F(s5)**-1
# Validate candidate
if k5_pred == k5_ecdsa:
found_d = d0
break
if found_d is not None:
flag = f"L3HCTF{{{int(found_d)}}}"
print("Flag:", flag)
else:
print("No valid d found")
RRRSSSAAA
from sage.all import *
from secret import flag
def generate_vulnerable_key(bits=1024):
p_bits = bits // 2
q_bits = bits - p_bits
while True:
p = random_prime(2**(p_bits), lbound=2**(p_bits-1))
q = random_prime(2**(q_bits), lbound=2**(q_bits-1))
if p != q and p > q and p < 2*q:
break
N = p * q
phi = (p**4 - 1) * (q**4 - 1)
d_bits = 1024
d_bound = 2**d_bits
while True:
d_small = randint(2, d_bound)
d = phi - d_small
if gcd(d, phi) == 1:
if d_small.bit_length() == 1021:
break
e = inverse_mod(d, phi)
return N, e
def encrypt(m, N, e):
n = 4
r = 2
R = Integers(N)
P = PolynomialRing(R, 't')
t = P.gen()
Q = P.quotient(t**n - r)
m_poly = Q([m, 0, 0, 0])
c_poly = m_poly ** e
return c_poly.lift()
if __name__ == "__main__":
N, e = generate_vulnerable_key()
m = int.from_bytes(flag, 'big')
c = encrypt(m, N, e)
print(f"N = {N}")
print(f"e = {e}")
print(f"c = {c}")
# N = 99697845285265879829811232968100099666254250525000506525475952592468738395250956460890611762459685140661035795964867321445992110528627232335703962897072608767840783176553829502743629914407970206513639916759403399986924602596286330464348286080258986075962271511105387188070309852907253486162504945490429185609
# e = 74900336437853271512557457581304251523854378376434438153117909482138661618901386551154807447783262736408028580620771857416463085746907317126876189023636958838207330193074215769008709076254356539808209005917645822989554532710565445155350102802675594603406077862472881027575871589046600011223990947361848608637247276816477996863812313225929441545045479384803449990623969591150979899801722841101938868710054151839628803383603849632857020369527380816687165487370957857737696187061619496102857237814447790678611448197153594917852504509869007597997670022501500067854210261136878917620198551551460145853528269270832725348151160651020188255399136483482428499340574623409209151124687319668989144444549871527949104436734300277004316939985015286758651969045396343970037328043635061226100170529991733947365830164811844853806681198818875837903563263114249814483901121700854712406832325690101810786429930813776784979083590353027191492894890551838308899148551566437532914838098811643805243593419063566975400775134981190248113477610235165151367913498299241375039256652674679958159505112725441797566678743542054295794919839551675786573113798857814005058856054462008797386322048089657472710775620574463924678367455233801970310210504653908307254926827
# c = 98460941530646528059934657633016619266170844887697553075379408285596784682803952762901219607460711533547279478564732097775812539176991062440097573591978613933775149262760936643842229597070673855940231912579258721734434631479496590694499265794576610924303262676255858387586947276246725949970866534023718638879
分析:要解密该加密系统并获取 flag,需要利用密钥生成过程中的漏洞。在 generate_vulnerable_key 函数中,私钥 \(d\) 被构造为 \(d = \phi - d_{\text{small}}\),其中 \(d_{\text{small}}\) 是一个较小的整数(位长度为 1021),而 \(\phi = (p^4 - 1)(q^4 - 1)\),\(N = p \times q\),且 \(p\) 和 \(q\) 是满足 \(q < p < 2q\) 的素数。公钥指数 \(e\) 是 \(d\) 对 \(\phi\) 的模逆。加密过程本质上是计算 \(c \equiv m^e \pmod{N}\)(因为输入是常数多项式,多项式环的操作简化为模 \(N\) 的指数运算)。 漏洞在于 \(d_{\text{small}}\) 较小(1021 位),而 \(\phi \approx N^4\)(约 4096 位),导致 \(e\) 和 \(N^4\) 的比值 \(\beta = e / N^4\) 非常接近有理数 \(m / s\),其中 \(s = d_{\text{small}}\),\(m\) 是整数。这允许通过连分数展开逼近 \(\beta\),找到候选的 \(s\) 和 \(m\),进而恢复 \(\phi\) 并分解 \(N\)。
exp:
from sage.all import *
import binascii
N = 99697845285265879829811232968100099666254250525000506525475952592468738395250956460890611762459685140661035795964867321445992110528627232335703962897072608767840783176553829502743629914407970206513639916759403399986924602596286330464348286080258986075962271511105387188070309852907253486162504945490429185609
e = 74900336437853271512557457581304251523854378376434438153117909482138661618901386551154807447783262736408028580620771857416463085746907317126876189023636958838207330193074215769008709076254356539808209005917645822989554532710565445155350102802675594603406077862472881027575871589046600011223990947361848608637247276816477996863812313225929441545045479384803449990623969591150979899801722841101938868710054151839628803383603849632857020369527380816687165487370957857737696187061619496102857237814447790678611448197153594917852504509869007597997670022501500067854210261136878917620198551551460145853528269270832725348151160651020188255399136483482428499340574623409209151124687319668989144444549871527949104436734300277004316939985015286758651969045396343970037328043635061226100170529991733947365830164811844853806681198818875837903563263114249814483901121700854712406832325690101810786429930813776784979083590353027191492894890551838308899148551566437532914838098811643805243593419063566975400775134981190248113477610235165151367913498299241375039256652674679958159505112725441797566678743542054295794919839551675786573113798857814005058856054462008797386322048089657472710775620574463924678367455233801970310210504653908307254926827
c = 98460941530646528059934657633016619266170844887697553075379408285596784682803952762901219607460711533547279478564732097775812539176991062440097573591978613933775149262760936643842229597070673855940231912579258721734434631479496590694499265794576610924303262676255858387586947276246725949970866534023718638879
def solve():
N4 = N**4
beta = e / N4
cf = continued_fraction(beta)
convs = cf.convergents()
for pkqk in convs:
pk = pkqk.numerator()
qk = pkqk.denominator()
if qk < 2**1020:
continue
if qk >= 2**1021:
break
if qk.nbits() != 1021:
continue
s = qk
m_val = pk
num = e * s + 1
if num % m_val != 0:
continue
phi_cand = num // m_val
T = N4 - phi_cand + 1
D = T**2 - 4 * N4
if D < 0:
continue
sqrtD = D.isqrt()
if sqrtD**2 != D:
continue
x1 = (T + sqrtD) // 2
x2 = (T - sqrtD) // 2
if x1 * x2 != N4:
continue
try:
p4 = max(x1, x2)
q4 = min(x1, x2)
p_cand = p4.nth_root(4)
q_cand = q4.nth_root(4)
if p_cand**4 != p4 or q_cand**4 != q4:
continue
if p_cand * q_cand != N:
continue
if not (p_cand.is_prime() and q_cand.is_prime()):
continue
p = p_cand
q = q_cand
print(f"Found p = {p}")
print(f"Found q = {q}")
phi = (p**4 - 1) * (q**4 - 1)
d = inverse_mod(e, phi)
m = pow(c, d, N)
m_bytes = int(m).to_bytes((m.bit_length() + 7) // 8, 'big')
flag = m_bytes.decode('utf-8', errors='ignore')
return flag
except (ValueError, TypeError):
continue
return "Decryption failed. No valid factors found."
if __name__ == "__main__":
flag = solve()
print(f"Flag: {flag}")
Misc
Please Sign In
import uvicorn
import torch
import json
import os
from fastapi import FastAPI, File, UploadFile
from PIL import Image
from torchvision import transforms
from torchvision.models import shufflenet_v2_x1_0, ShuffleNet_V2_X1_0_Weights
feature_extractor = shufflenet_v2_x1_0(weights=ShuffleNet_V2_X1_0_Weights.IMAGENET1K_V1)
feature_extractor.fc = torch.nn.Identity()
feature_extractor.eval()
weights = ShuffleNet_V2_X1_0_Weights.IMAGENET1K_V1
transform = transforms.Compose([
transforms.ToTensor(),
])
if not os.path.exists("embedding.json"):
user_image = Image.open("user_image.jpg").convert("RGB")
user_image = transform(user_image).unsqueeze(0)
with torch.no_grad():
user_embedding = feature_extractor(user_image)[0]
with open("embedding.json", "w") as f:
json.dump(user_embedding.tolist(), f)
user_embedding = json.load(open("embedding.json", "r"))
user_embedding = torch.tensor(user_embedding, dtype=torch.float32)
user_embedding = user_embedding.unsqueeze(0)
app = FastAPI()
@app.post("/signin/")
async def signin(file: UploadFile = File(...)):
submit_image = Image.open(file.file).convert("RGB")
submit_image = transform(submit_image).unsqueeze(0)
with torch.no_grad():
submit_embedding = feature_extractor(submit_image)[0]
diff = torch.mean((user_embedding - submit_embedding) ** 2)
result = {
"status": "L3HCTF{test_flag}" if diff.item() < 5e-6 else "failure"
}
return result
@app.get("/")
async def root():
return {"message": "Welcome to the Face Recognition API!"}
if __name__ == "__main__":
uvicorn.run(app, host="0.0.0.0", port=8000)
丢ai直接出来了:
服务器使用 shufflenet_v2_x1_0 模型提取上传图片的 embedding,并与 embedding.json 中的目标向量做 MSE 计算:
python复制编辑diff = torch.mean((user_embedding - submit_embedding) ** 2)
if diff.item() < 5e-6:
return flag
目标是构造一张图片,使其经过该模型后的 embedding 与目标向量尽可能接近,满足 diff 小于 5e-6。
我们使用 PyTorch 优化一个 224×224 的图像张量,使其 embedding 逼近目标向量。最终将图像保存为 PNG 格式并提交。
with open("embedding.json") as f:
target_embedding = torch.tensor(json.load(f)).unsqueeze(0)
model = shufflenet_v2_x1_0(weights=weights)
model.fc = torch.nn.Identity()
model.eval()
初始化图像张量
img_tensor = torch.full((1, 3, 224, 224), 0.5, requires_grad=True)
直接优化 transform 后的张量,避免 PIL 转换带来的不可导问题。
迭代优化
for i in range(500):
optimizer.zero_grad()
embedding = model(img_tensor.clamp(0, 1))
loss = loss_fn(embedding, target_embedding)
loss.backward()
optimizer.step()
使用 MSE 作为损失函数,使生成图像的 embedding 趋近目标向量。
保存并提交图像
clamped = img_tensor.detach().squeeze().clamp(0, 1)
pil_img = transforms.ToPILImage()(clamped)
pil_img.save(buf, format='PNG')
response = requests.post(url, files={'file': ('final.png', buf, 'image/png')})
使用 PNG 格式防止有损压缩带来的误差。
exp:
import torch
from torchvision.models import shufflenet_v2_x1_0, ShuffleNet_V2_X1_0_Weights
from torchvision import transforms
import json
import requests
from PIL import Image
import io
# ==== 加载 embedding ====
with open("embedding.json") as f:
target_embedding = torch.tensor(json.load(f)).unsqueeze(0)
# ==== 加载模型 ====
weights = ShuffleNet_V2_X1_0_Weights.IMAGENET1K_V1
model = shufflenet_v2_x1_0(weights=weights)
model.fc = torch.nn.Identity()
model.eval()
# ==== 直接优化 transform 后的输入张量 ====
# torch 的 ToTensor() 是将 PIL 转成 [0,1] float tensor
# 所以我们可以直接优化这种 tensor,跳过 PIL 环节(避免不可导)
img_tensor = torch.full((1, 3, 224, 224), 0.5, requires_grad=True)
optimizer = torch.optim.Adam([img_tensor], lr=0.01)
loss_fn = torch.nn.MSELoss()
# ==== 迭代优化 ====
for i in range(500):
optimizer.zero_grad()
embedding = model(img_tensor.clamp(0, 1)) # clamp 确保在 [0,1] 区间
loss = loss_fn(embedding, target_embedding)
loss.backward()
optimizer.step()
if i % 50 == 0 or loss.item() < 5e-6:
print(f"[{i}] loss = {loss.item():.10f}")
if loss.item() < 5e-6:
print(f"[+] Converged! Final loss = {loss.item():.10f}")
break
else:
print("[-] Not converged.")
# ==== 保存为 PNG 图像 ====
clamped = img_tensor.detach().squeeze().clamp(0, 1)
pil_img = transforms.ToPILImage()(clamped)
buf = io.BytesIO()
pil_img.save(buf, format='PNG')
buf.seek(0)
# ==== 上传到远程服务器 ====
url = "http://1.95.8.146:50001/signin/"
files = {'file': ('final.png', buf, 'image/png')}
response = requests.post(url, files=files)
print("[*] Server response:", response.text)
"""
[0] loss = 0.0002544475
[50] loss = 0.0000109611
[95] loss = 0.0000049663
[+] Converged! Final loss = 0.0000049663
[*] Server response: {"status":"L3HCTF{f4c3_r3c0gn1t10n_15_n0t_s0_s3cur3_4ft3r_4ll}"}
"""
PaperBack
搜索一下这个,还有题目提示I really like OllyDbg,直接搜索OllyDbg PaperBack得到
去下载这个工具,然后把点状图片拖进去
得到flag.ws,看到这个后缀就能想到是whitesnow隐写,可以在Whitelips the Esoteric Language IDE
上面解密
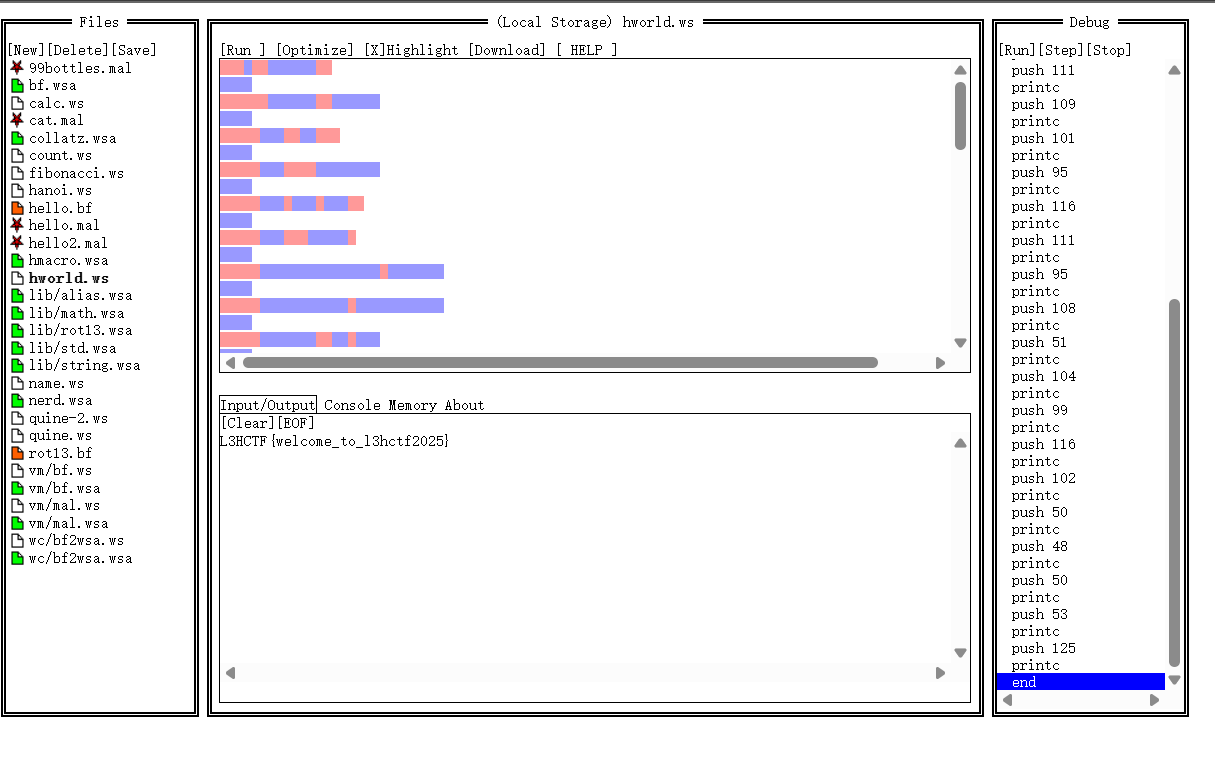
L3HCTF{welcome_to_l3hctf2025}
量子双生影
看到stream,又是rar压缩包,可以猜测存在ntfs流,用ntfsstreamseditor查看。
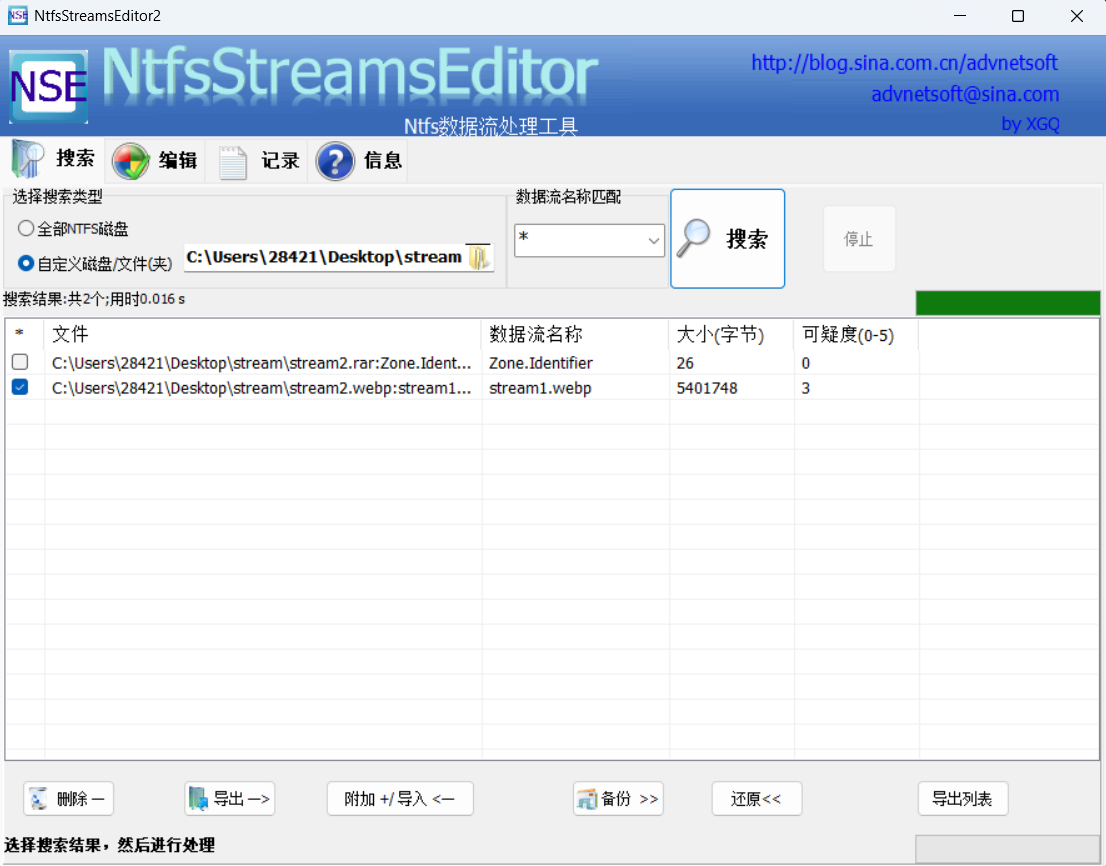
导出,双图异或得到答案

L3HCTF{Quantum_ADS_XOR}
Why not read it out?

这个狐狸语言真的,做了一天多。识图发现是tunic语言,但是用现有的翻译器根本翻译不出来。
用010editor打开,尾部有一个base,==wdllmdlJFIOdUSgoDduFDa,倒过来,解码是:
h1nt: IGN RevieA
然后我就找到这个网站,找到tunic专区,的review板块:
这两段句子和题目图片能一样对上

所以思路就是根据已知明文翻译下面的5个句子
但是我发现下面的狐语上面有的有有的没有,第一天晚上根据读音推到了
1.the ? of ? is: ? on ? ? fox
2. ???with??,??with?one
3.? ? ?with ? ?
4,make every ???
5,you????(word)
然后我看了一下b站的这个视频:https://www.bilibili.com/video/BV1n541117Pi
但是我用这个官方的方法去推已知明文的部分,发现对不上,所以这个狐语肯定改了规则。
没办法,所以尝试手搓发音规则来破译。因为这个语言就是基于元音和辅音来的。
用这个网站,将两段文字粘贴进去,根据音标的元辅来填空。

没错,开始手搓。
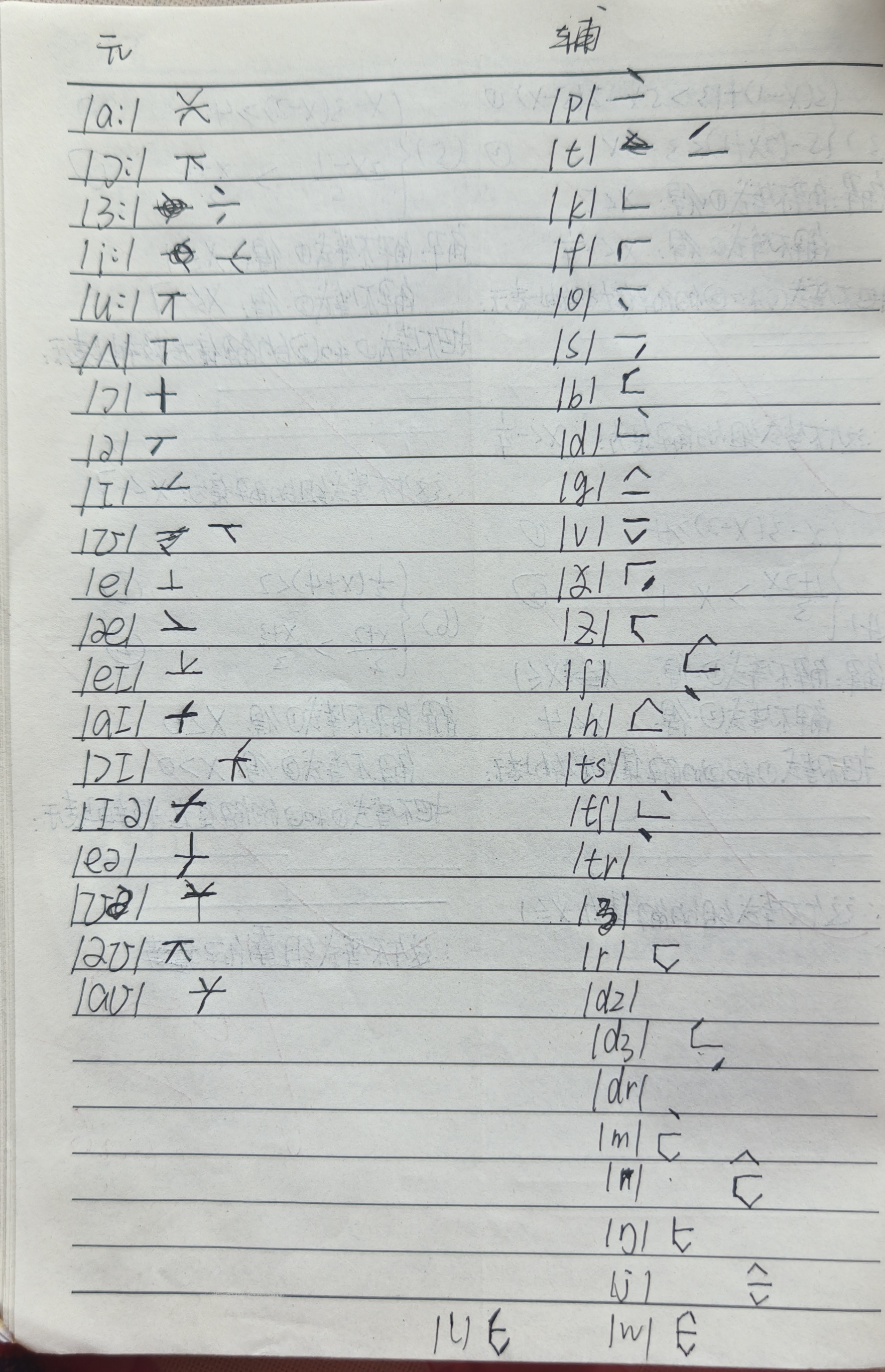
得到的发音规则是六边形里面是元音,外围是辅音,与正常版本相反。然后底下有圆圈的读音是先读元音。
翻译:
1.the content of flag is: come on little brave fox
2.replace letter o with number 0,letter l with number one
3.replace letter a with symbol at
4.make every letter e uppercase
5。use underline to link each word
L3HCTF{c0mE_0n_1itt1E_br@vE_f0x}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号