[六省联考2017]相逢是问候——欧拉定理+线段树

本题可能欧拉定理和欧拉公式混用，，其实是欧拉定理。欧拉公式是另外一个东西（欧拉太巨辣）

Description

信息将你我连结。B君希望以维护一个长度为n的数组，这个数组的下标为从1到n的正整数。一共有m个操作，可以

分为两种：0 l r表示将第l个到第r个数（al,al+1,...,ar）中的每一个数ai替换为c^ai，即c的ai次方，其中c是

输入的一个常数，也就是执行赋值ai=c^ai1 l r求第l个到第r个数的和，也就是输出：sigma(ai),l<=i<=rai因为

这个结果可能会很大，所以你只需要输出结果mod p的值即可。

Input

第一行有三个整数n,m,p,c，所有整数含义见问题描述。

接下来一行n个整数，表示a数组的初始值。

接下来m行，每行三个整数，其中第一个整数表示了操作的类型。

如果是0的话，表示这是一个修改操作，操作的参数为l,r。

如果是1的话，表示这是一个询问操作，操作的参数为l,r。

1 ≤ n ≤ 50000, 1 ≤ m ≤ 50000, 1 ≤ p ≤ 100000000, 0 < c <p, 0 ≤ ai < p

Output

对于每个询问操作，输出一行，包括一个整数表示答案mod p的值。

Solution：

也是比较恶心的题目了。

综合了数论（欧拉公式，phi的求法，快速幂）+数据结构（线段树）+预处理（phi的迭代，快速幂指数根号拆分）

一道值得好好做的好题。

首先我们要知道扩展欧拉定理：

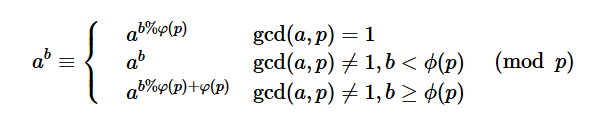
（温馨提示：

类似地有一道题：

上帝与集合的正确用法

这个题目是本题的简化简化简化简化。。。版。

先用扩展欧拉定理过了这道题才行。（虽然我用的CRT））

这个题目一看不可做

但是发现，根据扩展欧拉定理，即使有：

c^c^c^c^..^a

不断p取phi，大概logn次会变成1

证明：如果p是偶数，必然会至少有p/2个数不互质，会除以2

如果p是奇数，因为gcd(n,x)=gcd(n,n-x)=1,所以，与p互质的数成对出现，phi都是偶数（除了1,2）。p=phi(p)就变成了偶数。

每两次至少除以2

 

所以，一个位置最多被操作logp（设为up）次，值就不会再变了。因为若p=1时，根据欧拉公式第三条，指数一定都会是1。

所以，我们可以预处理每个位置操作up次后的值。

然后，区间修改，区间求和？线段树！

暴力区间修改，如果区间修改次数==up，则不再修改。

复杂度，大概：O(nlog^2n+mlogn)

 

细节问题：推荐：bzoj4869: [Shoi2017]相逢是问候（欧拉函数+线段树）

1.up要到Phi(1)=1，也就是说，如果p=4，要mod 4 、2、1 、1

因为，如果不mod两个1的话，可能会当ai=0时出锅。

例如：2^2^0 mod 4=2 这个时候，最上层是0mod1，我们就认为它不变了，后面就不会再操作。

而，如果再操作一次，2^2^2^0 mod 4=0 ，竟然还变化？

为什么？

思考，我们为什么可以mod1就停止了？

上述：“因为扩展欧拉定理第三条”，如果模数是1，那么x mod 1=0恒成立，然后第三条会加一个phi(1)=1，那么，这个模数1以上的（如果还有）部分，算完之后到1这里，都会 blablabla..  mod 1 +1 =1。

所以可以划线停止操作。

但是，别忘了第三条有一个适用条件，x>=1，但是，这个题c不是0，但是ai确实可能是0

所以，由于0<1  并不能用第三条，所以不能保证到这个phi(2)=1的时候，之后操作不会改变值。

 

那怎么办？

其实，只要再处理一层，由于c不会是0，那么其实是，$c^{c^{a\space mod 1}\space mod 1} mod 2$

即使a是0，那么：$c^{c^{0\space mod 1}\space mod 1} mod 2$而c^0=1

所以在底下的一个mod 1 +1之后，一定都是1了。即可划线。

 

2.欧拉函数的锅：

要ret=ret/i*(i-1) 不能ret=ret*(i-1)/i 后者瞬间爆int

我们经常习惯先乘后除（有时为了保证整除），但是在这里是一个会WA的习惯。注意这个容易错的细节。

 

3.预处理每个ai的操作dep层，上面递归返回的部分是否比当前的mod phi(p)大？

即：

这里面的mod p上层下来的tmp，究竟c^tmp比p大还是小呢？

而且，这个tmp可能还不能随便取mo。

直接快速幂？取模之后一定比p小还比较个毛线

我是这样做的（可能和别的题解不太一样）：

因为，p是一个1e9以内的数，而c是一个确定的数。

有一个定理是：$\forall x>1 : x^{\phi(p)}\ge p$

那么，其实我们上面的tmp可以直接对phi(p)等取模

证明：

因为，若满足第三条，一定有tmp>=phi(p)，而如果c>1,则不影响判断c^tmp与p的关系

如果不满足，本身就不会对phi(p)取模，也不会影响判断。

而且我们可以进一步发现，如果在某一层满足第三条，那么之后的每一个tmp都>=phi(p)，会一直以第三条满足下去！！

所以，满足第二条（即不取模）和满足第三条的层一定是连续的上下两段！！

证毕。

 

所以，我们可以每层都mod phi(p)并且不会影响大小比较。

那么，有了tmp，这一层怎么比较大小呢？

发现，当c>1时，tmp最多32，就超出了1e9（也就是p的最大值）

所以，我们可以预处理c的1~50次方。如果c^i超过了1e9，就赋值为-1

判断的时候，如果tmp>50或者ci[tmp]=-1或者ci[tmp]>=phi(p)，那么就满足第三条，快速幂后要加phi(p)

c=1可以特判

 

4.在我费了3h调完上述的WA之后，然后它无情地TLE了。

因为，我们预处理的ai操作up次，总共带3个logn，T飞了。

真的要这么慢吗？

考虑优化：

1.每个数少枚举几次up？不行，必须预处理up以内所有情况。

2.每次c^c^c^c...不从0开始？不行，没有递推性质。

3.快速幂能否省省？可以！！！！

指数是1e9的，不能直接预处理，但是我们可以分块打表！！

处理c^1~10000 mod phi(phi(..p))，

令t=c^10000，预处理t^1~10000 mod phi(phi(..p))

这样，要用到快速幂的时候，可以直接拼凑。

x^k=x^((k/10000)*10000+(k%10000))

省掉一个logn

 

总复杂度：O(nlog^2n)

 

完结撒花~！！

 

 

#include<bits/stdc++.h>
#define numb (ch^'0')
#define mid ((l+r)>>1)
using namespace std;
typedef long long ll;
const int N=50000+5;
ll n,m,p,c;
void rd(ll &x){
    char ch;x=0;
    while(!isdigit(ch=getchar()));
    for(x=numb;isdigit(ch=getchar());x=(x<<1)+(x<<3)+numb);
}
ll a[N];
int b[N];
int up;
int phi[N];
ll ci[N];
int ouler(ll x){
    int ret=x;
    for(int i=2;i*i<=x;i++){
        if(x%i==0){
            ret=ret/i*(i-1);
            while(x%i==0) x/=i;
        }
    }
    if(x>1) ret=ret/x*(x-1);
    return ret;
}
ll num[N][35];
ll qm(ll x,ll y,ll mod){
    ll ret=1%mod;
    while(y){
        if(y&1) (ret*=x)%=mod;
        (x*=x)%=mod;
        y>>=1;
    }
    return ret;
}
ll mi1[10005][35];
ll mi2[10005][35];
ll tim(int id,int dep,int lim){
    if(dep==lim){
        return a[id]<phi[dep]?a[id]:a[id]%phi[dep]+phi[dep];
    }
    ll tmp=tim(id,dep+1,lim);
    ll ret=0;
    if(c==1){
        ret=1;
        if(ret>=phi[dep]) ret=ret%phi[dep]+phi[dep];
    }else if(c==0){
        ret=1;
        if(ret>=phi[dep]) ret=ret%phi[dep]+phi[dep];
    }else{
        if(tmp>50) ret=(mi2[tmp/10000][dep]*mi1[tmp%10000][dep]%phi[dep])+phi[dep];
        else if(ci[tmp]<0||ci[tmp]>=phi[dep]) ret=(mi2[tmp/10000][dep]*mi1[tmp%10000][dep]%phi[dep])+phi[dep];
        else ret=(mi2[tmp/10000][dep]*mi1[tmp%10000][dep]%phi[dep]);
    }
    return ret;
}

struct node{
    ll mx,sum;
}t[N<<2];
void pushup(int x){
    t[x].sum=(t[x<<1].sum+t[x<<1|1].sum)%p;
    t[x].mx=max(t[x<<1].mx,t[x<<1|1].mx);
}
void build(int x,int l,int r){
    if(l==r){
        t[x].sum=a[l];
        t[x].mx=up;return;
    }
    build(x<<1,l,mid);build(x<<1|1,mid+1,r);
    pushup(x);
}
void chan(int x,int l,int r,int L,int R){
    if(L<=l&&r<=R){
        if(l==r) {
            t[x].mx=max(t[x].mx-1,(ll)0);
            t[x].sum=num[l][up-t[x].mx];
            return;
        }
        else{
            if(t[x<<1].mx>0) chan(x<<1,l,mid,L,R);
            if(t[x<<1|1].mx>0) chan(x<<1|1,mid+1,r,L,R);
            pushup(x);
            return;
        }
    }
    else{
        if(L<=mid) chan(x<<1,l,mid,L,R);
        if(mid<R) chan(x<<1|1,mid+1,r,L,R);
        pushup(x);
        return;
    }
}
ll query(int x,int l,int r,int L,int R){
    if(L<=l&&r<=R){
        return t[x].sum;
    }
    ll ret=0;
    if(L<=mid) (ret+=query(x<<1,l,mid,L,R))%=p;
    if(mid<R) (ret+=query(x<<1|1,mid+1,r,L,R))%=p;
    return ret;
}
int main(){
    rd(n);rd(m);rd(p);rd(c);
    ci[0]=1;
    for(int i=1;i<=50;i++){
        ci[i]=ci[i-1]*c;
        if(ci[i]>2e9) ci[i]=-1;
        if(ci[i]<0) ci[i]=-1;
    }
    
    int tmp=p;
    phi[0]=p;
    while(tmp!=1){
        up++;
        phi[up]=ouler(tmp);
        tmp=phi[up];
    }
    up++;phi[up]=tmp;
    
    for(int j=0;j<=up;j++){
        mi1[0][j]=1%phi[j];
        ll t=qm(c,10000,phi[j]);
        mi2[0][j]=1%phi[j];
        for(int i=1;i<=10000;i++){
            mi1[i][j]=qm(c,i,phi[j]);
            mi2[i][j]=qm(t,i,phi[j]);
        }
    }
    
    for(int i=1;i<=n;i++) rd(a[i]);
    for(int i=1;i<=n;i++) {
        num[i][0]=a[i];
        for(int j=1;j<=up;j++){
            num[i][j]=tim(i,0,j)%p;
        }
    }
    build(1,1,n);
    ll op,l,r;
    while(m--){
        rd(op);rd(l);rd(r);
        if(op){
            printf("%lld\n",query(1,1,n,l,r));
        }
        else{
            chan(1,1,n,l,r);
        }
    }
    return 0;
}

 

 总结：

怎么说，一道优秀的省选题就是这样。综合性强，代码要求也不小，细节多，数学难度也有。