2021年寒假训练题目合集
CodeForces - 1312F Attack on Red Kingdom
首先公平组合游戏,SG函数
考虑对每一个数的SG值。
$f[n][0/1/2]$表示状态,最多和$f[n-1]~f[n-5]$的状态有关系
连续5个f作为一组,所以,一旦出现连续5个$f[i]~f[i+4]$与之前的$f[j]~f[j+4]$一样,那么就之后就重复了。
所以可以找周期。理论上是$4^15$一次,但是实际上打表发现最多是36。。。
然后求出每个周期的值,再对应就行了。
对公平组合游戏要熟悉,转移方式比较少,用打表找周期。get!
CodeForces - 1321F Reachable Strings
考虑两个串什么时候可以互相表示
每个0都尽量往后移动,这样连续的两个1都能甩到最左边
所以,只要删掉所有相邻两个1,然后比较两个串是否相同即可。
用线段树,节点维护:1.删掉的pair数(可省) 2.删完以后的哈希值 3.删完后最后一个和第一个数是不是1(用于区间合并)
即可。
发现,变换是可逆的。所以先把两个串都向一个方向靠拢,再比较是否相同。
Codeforce 1293 F. Chaotic V.
首先只用考虑5000个点即可,每个点附加一个权重。
法一:
首先从1号点出发,先求出所有1!~5000!到1号点的距离。
然后不断走。如果使得重心更小就走下去。如果没有一个边使得重心会更小,那么就直接停止。
不断查看每个点是否是枚举根的子树。
每个阶乘再记录一下当前剩下的最大质因子和质因子次数。
复杂度O(5000*step) step是最后往下走的深度。
由于数会比较分散,所以step并不大。能过。
法二:
对于1!~5000!这些点建立虚树。虚树带权中心一定是虚树的一个节点。
求dfn序大小关系:假设dfs每次先遍历小的质因子。那么比较两个阶乘dfn序,只需要从最大质因子开始比就可以。
求lca,也是从最大质因子开始比,直到出现不一样的情况。
建虚树的同时,把边权(距离)也算出来。
然后也是用调整法求重心。
复杂度O(5000*cmp*logn) cmp是比较一次的代价。上界是1~5000质数个数,实际上均摊远远不到。
可过。
CodeForces 1293E Xenon's Attack on the Gangs
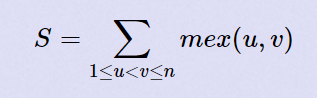
考虑每个边的贡献。那么必然要考虑从小到大给边赋值
通过不断的手玩,可以发现,0,1,2,3...尽量连在一起比较优秀。
并且,从小往大给边赋值的时候,一定是往当前链的最左或者最右放新边。
然后dp,f[i][j]表示,链i~j填0~len时的答案。枚举len边权放在最左还是最右即可。
至于怎么找”左右“,每个点当根dfs,求出fa[x][y]表示y作为根的时候,x的father是谁
O(n^2)
CodeForces 1370F The Hidden Pair
首先全部询问一遍,找到一个路径上的点x
然后以x为根,找到每个深度上的点的集合
二分较深关键点的距离。
找到较深关键点ans1之后,把ans1到x根上点除去。
用总距离减去dep[ans1],得到dep[ans2],把dep[ans2]的点(除了ans1到x的上的点)询问一遍
这样是12次
hard版上界是11次。而发现,二分下界可以是dis/2,上界是dis,这样就少了一次二分。
二分是个不错的思路。
开始只想着找到x之后,找子树走随机化路线,,,,不靠谱。
注意CF交互题的写法!!!!
1.printf询问、答案之后,都要fflush(stdout)
2.会返回x,d到输入文件里,需要再读取。
CodeForces 1200F Graph Traveler
mi很小。保留当前数值modulo lcm(1,2...10)即可。也就是mod 2520
如果又到了x,且数值mod 2520相同,那么必然已经走出了环。
f[1000][2520]表示,到了x,mod 2520的模数为p,最后的环上不同点的个数。
记忆化搜索即可。
用栈记录路径。
搜到循环节,暴力弹栈即可。

#include<bits/stdc++.h> #define reg register int #define il inline #define fi first #define se second #define mk(a,b) make_pair(a,b) #define numb (ch^'0') #define pb push_back #define solid const auto & #define enter cout<<endl #define pii pair<int,int> using namespace std; typedef long long ll; template<class T>il void rd(T &x){ char ch;x=0;bool fl=false;while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb);(fl==true)&&(x=-x);} template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');} template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');} template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');} namespace Modulo{ const int mod=998244353; il int ad(int x,int y){return x+y>=mod?x+y-mod:x+y;} il int sub(int x,int y){return ad(x,mod-y);} il int mul(int x,int y){return (ll)x*y%mod;} il void inc(int &x,int y){x=ad(x,y);} il void inc2(int &x,int y){x=mul(x,y);} il int qm(int x,int y=mod-2){int ret=1;while(y){if(y&1) ret=mul(x,ret);x=mul(x,x);y>>=1;}return ret;} template<class ...Args>il int ad(const int a,const int b,const Args &...args) {return ad(ad(a,b),args...);} template<class ...Args>il int mul(const int a,const int b,const Args &...args) {return mul(mul(a,b),args...);} } //using namespace Modulo; namespace Miracle{ const int N=1005; const int M=2520; int f[N][M]; int k[N],e[N][10]; int m[N]; int n; int rk[N][M]; int vis[N]; pii sta[N*M]; int top; int tot=0; int dfs(int x,int p){ if(f[x][p]) return f[x][p]; if(rk[x][p]){ int ret=0; pii z; do{ z=sta[top--]; if(!vis[z.fi]){ ++ret;vis[z.fi]=1; } }while(!(z.fi==x&&z.se==p)); rk[x][p]=0; return f[x][p]=ret; } rk[x][p]=++tot; ++top;sta[top].fi=x;sta[top].se=p; f[x][p]=dfs(e[x][(p+k[x])%m[x]],(p+k[x])%M); rk[x][p]=0; vis[x]=0; return f[x][p]; } int main(){ rd(n); for(int i=1;i<=n;++i){ rd(k[i]);k[i]=(k[i]%M+M)%M; } for(int i=1;i<=n;++i){ rd(m[i]); for(int j=0;j<m[i];++j){ rd(e[i][j]); } } int q; rd(q); int x,y; while(q--){ rd(x);rd(y); y=(y%M+M)%M; tot=0;top=0; printf("%d\n",dfs(x,y%M)); } return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* */
保留mod lcm的值,是一个思路。减轻状态数且保证正确性。
(和之前CF一个数位dp很像)
CF1288F Red-Blue Graph
考虑连接的B比R多怎么处理?
(开始的想法,都涂成B,再调整为R。但是本题还能不涂色。调整为R有2个变化,而调整为U,有1个变化。弄不了)
(ps:如果不能不涂色,那么也许我的方法能做。(反正题解方法肯定就做不了了))
处理方法:通过某个点流入和流出的流量大小关系即可。
二分图的边,左向右流 认为涂R,右向左流,认为涂B
如果左部点某点为R,就让S到这个点连流量[1,+oo]的边,表示流出的一定比流入的多。
其他三种情况同理。
然后跑 上下界费用流即可。

#include<bits/stdc++.h> #define reg register int #define il inline #define fi first #define se second #define mk(a,b) make_pair(a,b) #define numb (ch^'0') #define pb push_back #define solid const auto & #define enter cout<<endl #define pii pair<int,int> using namespace std; typedef long long ll; template<class T>il void rd(T &x){ char ch;x=0;bool fl=false;while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb);(fl==true)&&(x=-x);} template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');} template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');} template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');} namespace Modulo{ const int mod=998244353; il int ad(int x,int y){return x+y>=mod?x+y-mod:x+y;} il int sub(int x,int y){return ad(x,mod-y);} il int mul(int x,int y){return (ll)x*y%mod;} il void inc(int &x,int y){x=ad(x,y);} il void inc2(int &x,int y){x=mul(x,y);} il int qm(int x,int y=mod-2){int ret=1;while(y){if(y&1) ret=mul(x,ret);x=mul(x,x);y>>=1;}return ret;} template<class ...Args>il int ad(const int a,const int b,const Args &...args) {return ad(ad(a,b),args...);} template<class ...Args>il int mul(const int a,const int b,const Args &...args) {return mul(mul(a,b),args...);} } //using namespace Modulo; namespace Miracle{ const int N=404; const int inf=0x3f3f3f3f; int cnt=1; int n1,n2; int S,T; struct node{ int nxt,to; int w,c; }e[200000+5]; int hd[N]; char s[N]; void add(int x,int y,int w,int c){ e[++cnt].nxt=hd[x]; e[cnt].to=y; hd[x]=cnt; e[cnt].w=w;e[cnt].c=c; e[++cnt].nxt=hd[y]; e[cnt].to=x; hd[y]=cnt; e[cnt].w=0;e[cnt].c=-c; } int ans,mxflow; int du[N]; int dis[N],pre[N],incf[N]; int ss,tt; bool vis[N]; int pos[N]; queue<int>q; bool spfa(){ memset(dis,inf,sizeof dis); dis[ss]=0;incf[ss]=inf,pre[ss]=0; q.push(ss); while(!q.empty()){ int x=q.front();q.pop(); vis[x]=0; for(int i=hd[x];i;i=e[i].nxt){ int y=e[i].to; if(!e[i].w) continue; if(dis[y]>dis[x]+e[i].c){ dis[y]=dis[x]+e[i].c; incf[y]=min(incf[x],e[i].w); pre[y]=i; if(!vis[y]){ vis[y]=1; q.push(y); } } } } if(dis[tt]==0x3f3f3f3f) return false; return true; } void upda(){ int x=tt; ans+=incf[tt]*dis[tt]; mxflow+=incf[tt]; while(x!=ss){ e[pre[x]].w-=incf[tt]; e[pre[x]^1].w+=incf[tt]; x=e[pre[x]^1].to; } } int id(int fl,int c){ return fl*n1+c; } int main(){ rd(n1);rd(n2); int m;rd(m); int R,B;rd(R);rd(B); S=0,T=n1+n2+1; scanf("%s",s+1); for(int i=1;i<=n1;++i){ if(s[i]=='R'){ ++du[id(0,i)]; --du[S]; add(S,id(0,i),inf,0); }else if(s[i]=='B'){ --du[id(0,i)]; ++du[T]; add(id(0,i),T,inf,0); }else{ add(S,id(0,i),inf,0); add(id(0,i),T,inf,0); } } scanf("%s",s+1); for(int i=1;i<=n2;++i){ if(s[i]=='R'){ --du[id(1,i)]; ++du[T]; add(id(1,i),T,inf,0); }else if(s[i]=='B'){ ++du[id(1,i)]; --du[S]; add(S,id(1,i),inf,0); }else{ add(S,id(1,i),inf,0); add(id(1,i),T,inf,0); } } int x,y; for(int i=1;i<=m;++i){ rd(x);rd(y); pos[i]=cnt+1; add(id(0,x),id(1,y),1,R); add(id(1,y),id(0,x),1,B); } int up=0; for(int i=0;i<=n1+n2+1;++i){ if(du[i]>0) up+=du[i]; } add(T,S,inf,0); ss=n1+n2+2,tt=n1+n2+3; for(int i=0;i<=n1+n2+1;++i){ if(du[i]>0){ add(ss,i,du[i],0); }else if(du[i]<0){ add(i,tt,-du[i],0); } } while(spfa()) upda(); if(mxflow!=up){ puts("-1");return 0; } printf("%d\n",ans); for(int i=1;i<=m;++i){ if(e[pos[i]].w==0){ putchar('R'); }else if(e[pos[i]+2].w==0){ putchar('B'); }else putchar('U'); } return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* */
(也可以不用上下界,钦定-inf的权值。https://www.cnblogs.com/George1123/p/13685713.html)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号