bzoj3522: [Poi2014]Hotel

https://www.lydsy.com/JudgeOnline/problem.php?id=4543

bzoj 4543: [POI2014]Hotel加强版

 

n个点的无边权的树，树上找三个点，两两距离相同。

 

先说弱化版，n<=5000

原来我的做法是类似点分治的思路，但是并不能扩展

一个三个点的组其实是一个连通块，

我们考虑在连通块最上面的位置统计

要么x自己是一个点

要么x的son子树有一个，之前子树有两个，

要么x的son子树有两个，之前子树有一个

 

然后还要记录距离

f[x][j]x子树内，距离x为j的点的个数

g[x][j]，x子树内，距离x的点对(u,v)使得dis(u,lca)=dis(v,lca)=dis(x,lca)+j的点对的个数

转移方程：

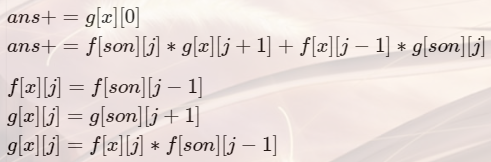
长链剖分优化即可

注意，g数组和f数组+1-1相反，所以g[son]=g[x]-1,f[son]=f[x]+1，开内存时候，前后开2倍

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
#define numb (ch^'0')
#define pb push_back
#define solid const auto &
#define enter cout<<endl
#define pii pair<int,int>
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){
    char ch;x=0;bool fl=false;while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*10+numb);(fl==true)&&(x=-x);}
template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');}
template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');}
namespace Modulo{
const int mod=998244353;
int ad(int x,int y){return (x+y)>=mod?x+y-mod:x+y;}
void inc(int &x,int y){x=ad(x,y);}
int mul(int x,int y){return (ll)x*y%mod;}
void inc2(int &x,int y){x=mul(x,y);}
int qm(int x,int y=mod-2){int ret=1;while(y){if(y&1) ret=mul(x,ret);x=mul(x,x);y>>=1;}return ret;}
}
//using namespace Modulo;
namespace Miracle{
const int N=100000+5;
ll memchi[4*N],*cur=memchi;
ll *f[N],*g[N];
int len[N],son[N];
int n;
struct node{
    int nxt,to;
}e[2*N];
int hd[N],cnt;
void add(int x,int y){
    e[++cnt].nxt=hd[x];
    e[cnt].to=y;
    hd[x]=cnt;
}
void dfs(int x,int fa){
    for(reg i=hd[x];i;i=e[i].nxt){
        int y=e[i].to;
        if(y==fa) continue;
        dfs(y,x);
        if(len[y]>len[son[x]]) son[x]=y;
    }
    len[x]=len[son[x]]+1;
}
ll ans;
void dp(int x,int fa){
    f[x][0]=1;
    if(son[x]) {
        f[son[x]]=f[x]+1;
        g[son[x]]=g[x]-1;
        dp(son[x],x);
    }
    ans+=g[x][0];
    for(reg i=hd[x];i;i=e[i].nxt){
        int y=e[i].to;
        if(y==fa||y==son[x]) continue;
        f[y]=cur;cur+=(len[y]<<1);
        g[y]=cur;cur+=(len[y]<<1);
        dp(y,x);
        for(reg j=0;j<len[y];++j){
            if(j+1<len[x]) ans+=f[y][j]*g[x][j+1];
            if(j) ans+=g[y][j]*f[x][j-1];
        }
        for(reg j=0;j<len[y];++j){
            if(j) g[x][j-1]+=g[y][j];
            if(j+1<len[x]) g[x][j+1]+=f[x][j+1]*f[y][j];
            f[x][j+1]+=f[y][j];
        }
    }
    
}
int main(){
    rd(n);
    int x,y;
    for(reg i=1;i<n;++i){
        rd(x);rd(y);
        add(x,y);add(y,x);
    }
    dfs(1,0);
    f[1]=cur;cur+=(len[1]<<1);
    g[1]=cur;cur+=(len[1]<<1);
    dp(1,0);
    // ot(ans);
    printf("%lld",ans);
    return 0;
}

}
signed main(){
    Miracle::main();
    return 0;
}

/*
   Author: *Miracle*
*/