CF889E Mod Mod Mod

CF889E Mod Mod Mod 

%%ywy

一种把状态减少，只保留有效状态的DP

 

首先，只和当前mod ai的值有关系，朴素的设法是：dp[i][j]，%ai=j的最总和是多少。

然而实在不方便转移

而注意到，xi一定是单调不升的，所以i位置是xi，那么ans可以表示为xi*i+b的形式。只用保留b即可

就是：

神仙的状态设计：dp[i][j]表示，第i位的x为j时，所谓的b最大是dp[i][j]

答案其实是i*x+dp[i][j]

显然也具有最优子结构的性质

而且一个性质是：dp[i][j]，随着j越来越小dp[i][j]单调不降。因为至少可以和dp[i][j]选择同样的b的结构！

 

考虑转移,i->i+1：思想：值域过大，尽量减少不必要的转移以减少状态数

我们用map存几个关键点，关键点之间的dp[][]值相同。

图像形如：

枚举关键点j，用dp[i][j]更新

首先发现，当j<a[i+1]时候，dp[i+1][j]max=dp[i][j]

否则，考虑用dp[i][j]来给[0,j]一起做转移，把这些dp[i][k]的dp都看做dp[i][j]，（由于dp[i][k]一定不小于dp[i][j]，就算这里转移小了，但是后面转移dp[i][<j]会考虑到的）

从k=j，k越来越小的时候，取模后也会越来越小，而我们认为这些k的dp[i][k]=dp[i][j]，所以只需要把j转移到dp[i+1][j%a[i+1]]过去即可，就是把关键点扔过去即可。

这样如果确实dp[i][k]=dp[i][j]的话，那么根据关键点定义，j%a[i+1]往下到下一个关键点的dp都一样，等价于dp[i][k]进行了转移。

 

而j越来越小的时候，

但是会mod到下一个循环节。也即k%a(i+1)=a(i+1)-1

对于y，<=j的最后一个%a(i+1)=a(i+1)-1的位置，也要进行转移。dp[i][j]->dp[i+1][a[i+1]-1]

正确性同理。

 

转移方程具体是：

 

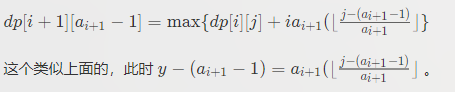
每个数只会mod logn次，一共有n个数，即a[1~n]-1

map进行滚动。

 总复杂度也是O(nlognlogx)

 

 

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
#define numb (ch^'0')
#define pb push_back
#define solid const auto &
#define enter cout<<endl
#define pii pair<int,int>
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){
    char ch;x=0;bool fl=false;while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*10+numb);(fl==true)&&(x=-x);}
template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');}
template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');}
namespace Modulo{
const int mod=998244353;
int ad(int x,int y){return (x+y)>=mod?x+y-mod:x+y;}
void inc(int &x,int y){x=ad(x,y);}
int mul(int x,int y){return (ll)x*y%mod;}
void inc2(int &x,int y){x=mul(x,y);}
int qm(int x,int y=mod-2){int ret=1;while(y){if(y&1) ret=mul(x,ret);x=mul(x,x);y>>=1;}return ret;}
}
//using namespace Modulo;
namespace Miracle{
const int N=200000+5;
int n;
ll a[N];
map<ll,ll,greater<ll> >mp;
ll tmp[5*N];
int main(){
    rd(n);
    for(reg i=1;i<=n;++i) rd(a[i]);
    mp[a[1]-1]=0;
    for(reg i=1;i<n;++i){
        int ptr=0;
        for(solid x:mp){
            if(x.fi<a[i+1]) break;
            mp[a[i+1]-1]=max(mp[a[i+1]-1],mp[x.fi]+(ll)i*a[i+1]*((x.fi-a[i+1]+1)/a[i+1]));
            mp[x.fi%a[i+1]]=max(mp[x.fi%a[i+1]],mp[x.fi]+(ll)i*(x.fi-x.fi%a[i+1]));
            tmp[++ptr]=x.fi;
        }
        while(ptr) mp.erase(tmp[ptr--]);
    }
    ll ans=0;
    for(solid x:mp){
        ans=max(ans,(ll)x.fi*n+x.se);
    }
    ot(ans);
    return 0;
}

}
signed main(){
    Miracle::main();
    return 0;
}

/*
   Author: *Miracle*
*/

 

同样的状态减少转移，有点类似分段函数

而dp[i][j]显然是前缀最小值，

所以，把[0,j]的dp都看成dp[i][j]，ans不会更大，而取max就覆盖了