一句话题解&&总结
CF79D Password:
差分。两点取反,本质是匹配!最短路+状压DP
取反是套路,匹配是发现可以把操作进行目的化和阶段化,从而第二次转化问题。
且匹配不会影响别的位置答案
sequence
计算最长极长段小于等于j的方案数
突破口是i,k总共对数nlogn级别,干掉j用组合意义大力推导
CF1062F Upgrading Cities
DAG考虑topo,关键性质:topo序队列中点两两不可达。只在队列长度<=2时候才关心。
CF1060F Shrinking Tree
考虑x是不是rt,要进行讨论的。考虑e什么时候合并,也是要讨论的。
x是不是rt就成了分界点。e什么时候合并也是关键点,这样才对son的子树内序列做出了限制。也才能用上dp[son]转移。
所以状态就直接记录还剩下多少个边没有合并,这些边都要注意是否有1/2的概率限制。而且还可知道之前放入了多少边,有助于组合数分配转移。
CF1009G Allowed Letters
贪心,后面有无解即可。完美匹配,Hall定理
[THUWC2017]随机二分图
考虑每个方案的出现概率和,f[S]进行记忆化爆搜。s偶数有用,状态数<=1e8
第2/3类边,看做独立的,再额外贡献+25%或者-25%的同时选择方案的系数。
拆边转化,然后同上!
【模板】第二类斯特林数·列
递推式:OGF,再不断迭代
根据定义:EGF,然后快速幂,
LOJ#6079. 「2017 山东一轮集训 Day7」养猫
k可重区间问题 的增强版:有上下界!
直接都选择s[i],然后再把一些调整到e[i]
考虑通过最大流的“最大”,使得至少每k个有me个e,也即选择少于k个,则不能保证流量最大
通过最大流的“上界”,限制每k个最多有k-ms个e
CF295E aroslav and Points
考虑每段的贡献,l*a*b,直接动态开点线段树维护∑l,∑al,∑bl,∑abl,pushup即可。答案就是∑abl
(不知为啥放到了图论专题)
CF1054F Electric Scheme
每行每列一条线,多于交点?每行每列点与点的间隔搞出来当做点,二分图,相交就inf连边,
CF757F Team Rocket Rises Again
最短路DAG+支配树
CF786E ALT
注意审题!所有守卫都要有一个狗!
所以直接最小割。连边倍增优化一下即可。
CF986F Oppa Funcan Style Remastered
转化为质因子的配凑,同余最短路!特判一些情况。
Atcoder某比赛题
给定p=1e6+3(一个质数),q(q<=1e5)次询问,每次给定n,d,x,求$Pi_{i=0}^{n-1}(x+i\times d)$
智商题
提出$d^n$,然后就是$d^n\times Pi_{i=0}^{n-1}(\frac{x}{d}+i)$
Atcoder Dark Horse
晋级的比拼是一个深度为n的满二叉树,1号获胜,当且到根路径的其余2^i(0<=i<=15)的分支最小值都不能是ai
都不能其实很难保证。考虑容斥。ai从大到小排序
f[i][s],前i个ai,钦定了|s|个作为s这个集合的分支子树的最小值。转移时候,分配给若干比ai大的编号即可。
然后ans+=(-1)^|s|*f[n][s]*....进行容斥即可。
然后这个只是分组,再乘上2^n*((2^i)!)才是答案。

#include<bits/stdc++.h> #define reg register int #define il inline #define fi first #define se second #define mk(a,b) make_pair(a,b) #define numb (ch^'0') #define pb push_back #define solid const auto & #define enter cout<<endl #define pii pair<int,int> using namespace std; typedef long long ll; template<class T>il void rd(T &x){ char ch;x=0;bool fl=false;while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb);(fl==true)&&(x=-x);} template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');} template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');} template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');} namespace Modulo{ const int mod=1e9+7; int ad(int x,int y){return (x+y)>=mod?x+y-mod:x+y;} void inc(int &x,int y){x=ad(x,y);} int mul(int x,int y){return (ll)x*y%mod;} void inc2(int &x,int y){x=mul(x,y);} int qm(int x,int y=mod-2){int ret=1;while(y){if(y&1) ret=mul(x,ret);x=mul(x,x);y>>=1;}return ret;} } using namespace Modulo; namespace Miracle{ const int N=17; const int M=(1<<16)+233; int jie[M],inv[M]; int C(int n,int m){ if(n<0||m<0||n<m) return 0; return mul(jie[n],mul(inv[m],inv[n-m])); } int f[N][1<<16]; int n,m; int a[N]; int sz[1<<16]; bool cmp(int x,int y){ return x>y; } int main(){ rd(n);rd(m); for(reg i=1;i<=m;++i) rd(a[i]); sort(a+1,a+m+1,cmp); jie[0]=1; for(reg i=1;i<=(1<<n);++i) jie[i]=mul(jie[i-1],i); inv[1<<n]=qm(jie[1<<n]); for(reg i=(1<<n)-1;i>=0;--i) inv[i]=mul(inv[i+1],i+1); for(reg i=0;i<(1<<n);++i){ sz[i]=sz[i>>1]*2+(i&1); } f[0][0]=1; for(reg i=1;i<=m;++i){ // cout<<"i "<<a[i]<<endl; for(reg s=0;s<(1<<n);++s){ if(f[i-1][s]==0) continue; f[i][s]=ad(f[i][s],f[i-1][s]); for(reg p=0;p<n;++p){ if(!((s>>p)&1)){ // cout<<" fang "<<s<<" and "<<p<<" : "<<mul(f[i-1][s],C((1<<n)-a[i]-sz[s],(1<<p)-1))<<endl; f[i][s|(1<<p)]=ad(f[i][s|(1<<p)],mul(f[i-1][s],C((1<<n)-a[i]-sz[s],(1<<p)-1))); // cout<<"go "<<(s|(1<<p))<<" "<<f[i][s|(1<<p)]<<endl; } } } } ll ans=0; for(reg s=0;s<(1<<n);++s){ int tmp=f[m][s]; // cout<<" s "<<s<<" tmp "<<tmp<<endl; int re=(1<<n)-sz[s]-1; for(reg p=0;p<n;++p){ if(!((s>>p)&1)){ tmp=mul(tmp,C(re,(1<<p))); re-=(1<<p); } } // cout<<" after "<<tmp<<endl; if(__builtin_popcount(s)&1){ tmp=mod-tmp; } ans=ad(ans,tmp); } // cout<<"ans1111 "<<ans<<endl; ans=mul(ans,(1<<n)); for(reg i=0;i<n;++i){ ans=mul(ans,jie[1<<i]); } ot(ans); return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* */
AT2000 Leftmost Ball
考虑多少种最终序列,直接从构造最终序列入手。
其实,最终序列里,白色球是左括号,每个颜色第一次出现的位置是右括号。就是一个括号匹配
f[i][j],后[i,n]里,j个右括号方案数,每填一个右括号,那么后面的k-2个球直接小球放盒子分配即可。
k=1特判。
至于为何是“后[i,n]”而不是前,因为这样放右括号时一定知道后面有多少个“盒子”

#include<bits/stdc++.h> #define reg register int #define il inline #define fi first #define se second #define mk(a,b) make_pair(a,b) #define numb (ch^'0') #define pb push_back #define solid const auto & #define enter cout<<endl #define pii pair<int,int> using namespace std; typedef long long ll; template<class T>il void rd(T &x){ char ch;x=0;bool fl=false;while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb);(fl==true)&&(x=-x);} template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');} template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');} template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');} namespace Modulo{ const int mod=1e9+7; int ad(int x,int y){return (x+y)>=mod?x+y-mod:x+y;} void inc(int &x,int y){x=ad(x,y);} int mul(int x,int y){return (ll)x*y%mod;} void inc2(int &x,int y){x=mul(x,y);} int qm(int x,int y=mod-2){int ret=1;while(y){if(y&1) ret=mul(x,ret);x=mul(x,x);y>>=1;}return ret;} } using namespace Modulo; namespace Miracle{ const int N=2002; const int M=4000000+5+N+N; int n,k; int f[2][N]; int jie[M],inv[M]; int C(int n,int m){ if(n<0||m<0||n<m) return 0; return mul(jie[n],mul(inv[m],inv[n-m])); } int main(){ rd(n);rd(k); if(k==1){ puts("1");return 0; } int lim=n*k+n+n; jie[0]=1; for(reg i=1;i<=lim;++i) jie[i]=mul(jie[i-1],i); inv[lim]=qm(jie[lim]); for(reg i=lim-1;i>=0;--i) inv[i]=mul(inv[i+1],i+1); int tmp=0; f[0][0]=1; for(reg i=2*n;i>=1;--i){ tmp^=1; memset(f[tmp],0,sizeof f[tmp]); int re=2*n-i; for(reg j=0;j<=min(re,n);++j){ if(!f[tmp^1][j]) continue; int le=re-j; if(le+1<=j) f[tmp][j]=ad(f[tmp][j],f[tmp^1][j]); if(j!=n){ f[tmp][j+1]=ad(f[tmp][j+1],mul(f[tmp^1][j],C(k-2+le+j*(k-1),le+j*(k-1)))); } } } ll ans=mul(f[tmp][n],jie[n]); ot(ans); return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* */
AT3576 Popping Balls
好题!考虑蓝色球的放置,s和t的最优位置来统计每个方案
CF1169B Pairs
被B题干掉了。。。
其实很简单。如果存在(a,b),(c,d)四个数都不同的数对,必然决策是两个数对各选择一个。
如果不存在,那么意味着,选择(a,b),剩下的都至少和a,b之一有交点,一定有解!

#include<bits/stdc++.h> #define reg register int #define il inline #define fi first #define se second #define mk(a,b) make_pair(a,b) #define numb (ch^'0') #define pb push_back #define solid const auto & #define enter cout<<endl #define pii pair<int,int> using namespace std; typedef long long ll; template<class T>il void rd(T &x){ char ch;x=0;bool fl=false;while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb);(fl==true)&&(x=-x);} template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');} template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');} template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');} namespace Modulo{ const int mod=998244353; int ad(int x,int y){return (x+y)>=mod?x+y-mod:x+y;} void inc(int &x,int y){x=ad(x,y);} int mul(int x,int y){return (ll)x*y%mod;} void inc2(int &x,int y){x=mul(x,y);} int qm(int x,int y=mod-2){int ret=1;while(y){if(y&1) ret=mul(x,ret);x=mul(x,x);y>>=1;}return ret;} } //using namespace Modulo; namespace Miracle{ const int N=3e5+5; int x[N],y[N]; int a,b,c,d; int n,m; bool che(int a,int b){ for(reg i=1;i<=m;++i){ if(x[i]!=a&&x[i]!=b&&y[i]!=a&&y[i]!=b) return false; } return true; } int main(){ rd(n);rd(m); for(reg i=1;i<=m;++i){ rd(x[i]);rd(y[i]); } a=x[1],b=y[1]; for(reg i=2;i<=m;++i){ if(x[i]!=a&&x[i]!=b&&y[i]!=a&&y[i]!=b){ c=x[i],d=y[i]; } } if(che(a,b)||che(a,c)||che(a,d)||che(b,c)||che(b,d)) puts("YES"); else puts("NO"); return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* */
CF860E Arkady and a Nobody-men
同层的处理lca,dfs序排序后,lca深度单调!单调栈维护即可!
CF685B Kay and Snowflake
子树重心一定在重儿子子树内。不断往上爬直到合法。复杂度O(重链总长度)=O(n)
51nod1766
唉降智了。五级题都不会
点集到点集的最大值。边权为正数
一个常用的套路:一个树上点集的直径,可以直接合并两个集合得到。四个端点C(4,2)计算即可。
另一个常用套路:编号区间?线段树!线段树区间维护这个区间的直径两个端点即可。
注意,询问的时候不能从[a,b]和[c,d]内部取max

#include<bits/stdc++.h> #define reg register int #define il inline #define fi first #define se second #define mk(a,b) make_pair(a,b) #define numb (ch^'0') #define pb push_back #define solid const auto & #define enter cout<<endl #define pii pair<int,int> using namespace std; typedef long long ll; template<class T>il void rd(T &x){ char ch;x=0;bool fl=false;while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb);(fl==true)&&(x=-x);} template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');} template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');} template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');} namespace Modulo{ const int mod=998244353; int ad(int x,int y){return (x+y)>=mod?x+y-mod:x+y;} void inc(int &x,int y){x=ad(x,y);} int mul(int x,int y){return (ll)x*y%mod;} void inc2(int &x,int y){x=mul(x,y);} int qm(int x,int y=mod-2){int ret=1;while(y){if(y&1) ret=mul(x,ret);x=mul(x,x);y>>=1;}return ret;} } //using namespace Modulo; namespace Miracle{ const int N=200000+5; int n,m; struct node{ int nxt,to,val; }e[2*N]; int hd[N],cnt; void add(int x,int y,int z){ e[++cnt].nxt=hd[x]; e[cnt].to=y;e[cnt].val=z; hd[x]=cnt; } int a[2*N],dfn[N],lp; int dep[N],dis[N]; int lg[2*N]; int f[2*N][18]; void dfs(int x,int fa){ dep[x]=dep[fa]+1; a[++lp]=x; dfn[x]=lp; for(reg i=hd[x];i;i=e[i].nxt){ int y=e[i].to; if(y==fa) continue; dis[y]=dis[x]+e[i].val; dfs(y,x); a[++lp]=x; } } int cmp(int x,int y){ return dep[x]<dep[y]?x:y; } int lca(int x,int y){ if(x==y) return x; x=dfn[x],y=dfn[y]; if(x>y) swap(x,y); int len=lg[y-x+1]; return cmp(f[x][len],f[y-(1<<len)+1][len]); } int dist(int x,int y){ return dis[x]+dis[y]-2*dis[lca(x,y)]; } struct tr{ int p[2]; int mx; tr(){ p[0]=p[1]=0;mx=0; } }t[4*N]; #define ls (x<<1) #define rs (x<<1|1) #define mid ((l+r)>>1) tr merge(tr a,tr b){ tr ret; if(a.mx>b.mx) ret=a; else ret=b; for(reg i=0;i<=1;++i){ for(reg j=0;j<=1;++j){ int lp=dist(a.p[i],b.p[j]); if(lp>ret.mx){ ret.p[0]=a.p[i],ret.p[1]=b.p[j];ret.mx=lp; } } } return ret; } tr con(tr a,tr b){ tr ret; for(reg i=0;i<=1;++i){ for(reg j=0;j<=1;++j){ int lp=dist(a.p[i],b.p[j]); if(lp>ret.mx){ ret.p[0]=a.p[i],ret.p[1]=b.p[j];ret.mx=lp; } } } return ret; } void pushup(int x){ t[x]=merge(t[ls],t[rs]); } void build(int x,int l,int r){ if(l==r){ t[x].p[0]=t[x].p[1]=l;t[x].mx=0;return; } build(x<<1,l,mid); build(x<<1|1,mid+1,r); pushup(x); } tr query(int x,int l,int r,int L,int R){ if(L<=l&&r<=R) return t[x]; if(L>mid) return query(rs,mid+1,r,L,R); if(R<=mid) return query(ls,l,mid,L,R); return merge(query(ls,l,mid,L,R),query(rs,mid+1,r,L,R)); } int main(){ rd(n); int x,y,z; for(reg i=1;i<n;++i){ rd(x);rd(y);rd(z); add(x,y,z);add(y,x,z); } dfs(1,0); for(reg i=1;i<=lp;++i){ lg[i]=(i>>(lg[i-1]+1))?lg[i-1]+1:lg[i-1]; f[i][0]=a[i]; } for(reg j=1;j<=17;++j){ for(reg i=1;i+(1<<j)-1<=lp;++i){ f[i][j]=cmp(f[i][j-1],f[i+(1<<(j-1))][j-1]); } } build(1,1,n); rd(m); int a,b,c,d; while(m--){ rd(a);rd(b);rd(c);rd(d); tr k=con(query(1,1,n,a,b),query(1,1,n,c,d)); printf("%d\n",k.mx); } return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* */
AT3912 Antennas on Tree
性质题,考虑k个点的连通块,当且仅当,连通块外的点形成若干条链且每个关键点最多与一个外部点相连。贪心即可。
51nod 1538
相当于一些球的序列,每种颜色的球有价值ai,价值总和是m的方案数
枚举最后一个球的颜色f[n]=∑f[n-ai]
线性递推即可。
CF643E Bear and Destroying Subtrees
emmm
f[x][i]表示x子树深度<=i的概率,$f[x][i]=\Pi0.5*(f[y][i-1]+1)$
精度<=1e-6,所以i只用记录到60即可,后面概率几乎为0
添加新点的时候暴力更新60个祖先。

#include<bits/stdc++.h> #define reg register int #define il inline #define fi first #define se second #define mk(a,b) make_pair(a,b) #define numb (ch^'0') #define pb push_back #define solid const auto & #define enter cout<<endl #define pii pair<int,int> using namespace std; typedef long long ll; template<class T>il void rd(T &x){ char ch;x=0;bool fl=false;while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb);(fl==true)&&(x=-x);} template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');} template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');} template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');} namespace Modulo{ const int mod=998244353; il int ad(int x,int y){return x+y>=mod?x+y-mod:x+y;} il int sub(int x,int y){return ad(x,mod-y);} il int mul(int x,int y){return (ll)x*y%mod;} il void inc(int &x,int y){x=ad(x,y);} il void inc2(int &x,int y){x=mul(x,y);} il int qm(int x,int y=mod-2){int ret=1;while(y){if(y&1) ret=mul(x,ret);x=mul(x,x);y>>=1;}return ret;} template<class ...Args>il int ad(const int a,const int b,const Args &...args) {return ad(ad(a,b),args...);} template<class ...Args>il int mul(const int a,const int b,const Args &...args) {return mul(mul(a,b),args...);} } // using namespace Modulo; #define ld long double namespace Miracle{ const int N=500000+5; const int M=60; int q,n; ld f[N][62]; int fa[N]; int main(){ rd(q); int op,x; n=1;f[n][0]=1; for(reg i=1;i<=M;++i) f[n][i]=1; while(q--){ rd(op);rd(x); if(op==1){ ++n;fa[n]=x; for(reg i=0;i<=M;++i) f[n][i]=1; ld tp=f[x][0]; f[x][0]*=0.5; int o=1; int las=x; x=fa[x]; while(x&&o<=M){ ld lp=f[x][o]; f[x][o]/=(0.5*tp+0.5); f[x][o]*=(0.5*f[las][o-1]+0.5); las=x; tp=lp; x=fa[x];++o; } }else{ ld ans=f[x][0]*0; for(reg i=1;i<=M;++i){ ans+=(f[x][i]-f[x][i-1])*i; } double lp=ans; printf("%.10lf\n",lp); } } return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* */
取max期望,可以记录每个达到值的概率
开不下?保留60个。。。一种无聊也有用的trick
AT2705 Yes or No
决策只和当前对错剩下的个数大小关系有关,相同的时候随机选择。
等价于在图上走,在不同位置决策不同
而路径只和实际答案对错的排列有关。
每个路径概率都是一样的。
统计每个路径的答案和。
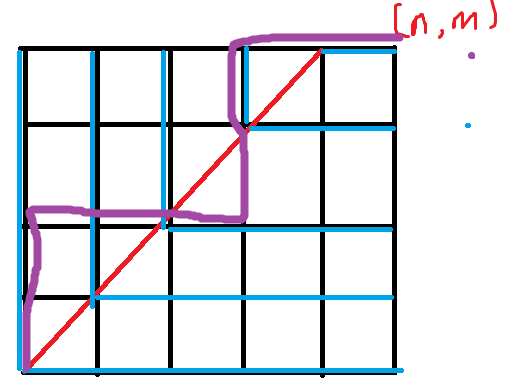
蓝色表示决策
不论对于什么路径,一定会覆盖max(n,m)个蓝色的段,至少是max(n,m)
对于y=x的,1/2概率正确。
统计所有路径经过y=x的次数的和。枚举每个(i,i)的点,统计经过的路径条数即可。
神奇
AT2062 ~K Perm Counting
容斥,统计至少j个不合法的
但是相差k是可能有冲突,所以每2×k个单独考虑
f[i][j][0/1]最后一个有没有选择上面的。类似分组背包做一下。
AT2370 Piling Up
naive地,设f[i][j]表示,剩下i轮,目前有j个白球所有方案数。
显然转移是横着走,往右下(白白),往右上(黑黑)三种。横着走可能有两种走法(白黑,黑白)
两个方案不同,当且仅当折线形状不同,或者横着走的两种走法选择不同。
会算重。
套路地,考虑在某个位置钦定统计:规定必须这个折线途中一次选择会使得白球个数为0
f[i][j][0/1]
转移即可。
tip:0/1是或的关系转移,用i-1更新i更好写。
(但我不是这样写的2333)

#include<bits/stdc++.h> #define reg register int #define il inline #define fi first #define se second #define mk(a,b) make_pair(a,b) #define numb (ch^'0') #define pb push_back #define solid const auto & #define enter cout<<endl #define pii pair<int,int> using namespace std; typedef long long ll; template<class T>il void rd(T &x){ char ch;x=0;bool fl=false;while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb);(fl==true)&&(x=-x);} template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');} template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');} template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');} namespace Modulo{ const int mod=1e9+7; il int ad(int x,int y){return x+y>=mod?x+y-mod:x+y;} il int sub(int x,int y){return ad(x,mod-y);} il int mul(int x,int y){return (ll)x*y%mod;} il void inc(int &x,int y){x=ad(x,y);} il void inc2(int &x,int y){x=mul(x,y);} il int qm(int x,int y=mod-2){int ret=1;while(y){if(y&1) ret=mul(x,ret);x=mul(x,x);y>>=1;}return ret;} template<class ...Args>il int ad(const int a,const int b,const Args &...args) {return ad(ad(a,b),args...);} template<class ...Args>il int mul(const int a,const int b,const Args &...args) {return mul(mul(a,b),args...);} } using namespace Modulo; namespace Miracle{ const int N=3003; int n,m; int f[N][N][2]; int main(){ rd(n);rd(m); for(reg i=0;i<=n;++i) f[0][i][0]=1; for(reg i=1;i<=m;++i){ for(reg j=0;j<=n;++j){ inc(f[i][j][0],ad((j!=n)*f[i-1][j][0],(j!=1&&j!=0)*f[i-1][j][0])); inc(f[i][j][1],ad((j!=n)*f[i-1][j][1],(j!=0)*f[i-1][j][1],(j==1)*(f[i-1][j][0]))); inc(f[i][j][0],ad((j!=n)*f[i-1][j+1][0],(j!=0&&j!=1)*f[i-1][j-1][0])); inc(f[i][j][1],ad((j!=n)*f[i-1][j+1][1],(j!=0)*f[i-1][j-1][1],(j==1)*f[i-1][j-1][0])); } } int ans=0; inc(f[m][0][1],f[m][0][0]); for(reg j=0;j<=n;++j){ inc(ans,f[m][j][1]); } ot(ans); return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* */
TCO14 Wildcard CountTables
TCO14 Wildcard CountTables——斯特林数+容斥
[HEOI2013]ALO
我怎么这么zz啊
枚举次大值x,次大值存在于两个极长的区间,和左边第一个/第二个,右边第一个/第二个比x大的有关系.可以从小到大排序,链表维护前驱后继,删除。
可持久化trie即可.
[AGC031E]
https://atcoder.jp/contests/agc031/tasks/agc031_e
好题
如果x,y只有一个方向限制,那么两个链反着连边即可(前缀后缀)。
各有两个方向?
枚举一共选择k个
那么右侧<=lim等价于左侧>=k-lim
成功转化为一侧!
有源汇上下界最大费用最大流即可。



策略:沿着一个路一直走,如果碰到断边,直接走到T的最短路,代价是所有断边情况的最大值。
如果能处理好一条邻边断了的最短路,dijkstra类似的Dp转移即可。
带修最短路问题,考虑最短路树
一条邻边断了,一定是最短路树往子树走再出去。
可并堆。(或者二维数点也可以)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号