小知识点随手记
1.组合数
∑C(n,i)^2=∑C(n,i)*C(n,n-i)=C(2n,n)就是从n劈一半，左边选择i个右边选择n-i个
2.>>1和/2的区别
在除不尽的时候，/2向中取整，>>1向下取整
所以线段树的时候如果下标是负数，那么一定要>>1！！！
否则[-1,0]就死循环了。
3.约瑟夫问题
快速找到下一个，重新标号
第i次，第M个人die：
f[i]剩下i个人，从0~i-1标号存活下来的人编号;f[i]=(f[i-1]+M+1)%i，就是平移过去重新标号，对应回原来的标号
f[1]=0
第i次，第i个人die
修改这次死亡的人报号
f[i]=(f[i-1]+(N-i+1)+1)%i
4.FFT爆精度？
主要是buf*gen会爆，因为是一个<1的数的几十万次方
（别的爆了也没办法了）
解决方法：
1.开long double
2.直接用cos()sin()计算。但是每次找太慢，所以预处理单位根的次方
5.块状链表
结构体维护每一个链表节点（块）
必要时合并删除
一般的插入删除可以用splay干掉
和分块有关的插入删除，就用块状链表了
6.unsigned long long比一般模数的hash冲突概率小
因为模数大啊。。随机情况卡掉概率太低了
但是1e9+7这种单模数随机情况都可能被卡
7.半平面交对偶凸壳
http://trinkle.blog.uoj.ac/blog/235
半开放的，可以求凸壳
封闭图形，还是直接半平面交好了
8.多项式清空
只要把涉及到的长度范围都清空即可。一般是2*n的范围清空。（主要还是看乘出来是多长的）
9.矩形加矩形求和
n,m<=1e5，时限2~3s？
不能直接树套树
二维差分+树状数组套线段树
一维差分+树状数组套线段树
都是统计每个差分后的标记再求前缀和的前缀和的时候的贡献
然后列出式子，可以把式子还是差分！带权打上标记。
二维差分要4*4个
一维差分要2*2个，但是自带2倍常数，所以常数相同的。
（或者线段树套线段树，其实更慢）
10.懒惰删除堆自带的bug
必须要使得决策堆和删除堆的元素的相对顺序是一样的！
小于号重载充分！不能出现决策堆A,B,删除堆B,A的情况！
小于号重载充分的话：
使得除非二者完全相等，否则必须有固定的大小顺序（未定义的话会有很多相等，比较就是随机的）
这样才能使得两个堆的相对位置相同。
11.平面图转对偶图
边数<=3*n-6
pf：
所以对偶图的点数最多是2*n的
12.树上回滚莫队
13.Trie上建EXSAM
必须用BFS！！
否则：
dfs倒序回来，每个B会扫整个链一遍就凉了。
14.连乘积反演
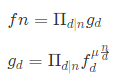
证明：直接ln，反演，再exp
15.凸包
相邻两个点都可以配凑出和为1的系数然后合并成一个点。最后一定可以合并出(A,B)
16.基环树计数？
1.直接枚举n个点n条边的连通块数量O(n^3logn)
2.枚举环大小，统计森林，再进行连边O(n^2logn)
3.被lx爆踩了。直接枚举环和环上的点，然后看成一个点，
利用prufer序列森林形成一个树的结论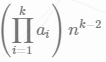
进行连接即可。
预处理n次幂，O(n)即可
17.小Trick：离线求逆元
求出所有的总乘积的逆元inv，s是前缀积，b是后缀积，则ni[i]=s[i]*b[i]*inv
O(n+log(mod))
18.钩子公式
问题:若干行,每行hi个人,每个人必须比左边和下边的人编号大,问方案数
结论:$ans=\frac{(\sum h_i)!}{\Pi h_i}$
19.Linux查RE
终端编译时候g++ my.cpp -o my -fsanitize=address -ftrapv
20.
