深度学习之激活函数
什么是激活函数
概念
要了解什么是激活函数,首先要了解神经网络模型的基本工作原理。
所谓激活函数(Activation Function),就是在人工神经网络的神经元上运行的函数,负责将神经元的输入映射到输出端。信号从一个神经元进入,经过非线性的激活函数,传入到下一层神经元;再经过该层神经元的激活,继续往下传递,如此循环往复,直到输出层。正是由于这些非线性函数的反复叠加,才使得神经网络有足够的capacity来抓取复杂的pattern,在各个领域取得state-of-the-art的结果。显而易见,激活函数在深度学习中举足轻重,也是很活跃的研究领域之一。
作用
激活函数的主要作用是提供网络的非线性建模能力。如果没有激活函数,那么该网络仅能够表达线性映射,此时即便有再多的隐藏层,其整个网络跟单层神经网络也是等价的。因此也可以认为,只有加入了激活函数之后,深度神经网络才具备了分层的非线性映射学习能力。 那么激活函数应该具有什么样的性质呢?
性质
- 可微性: 当优化方法是基于梯度的时候,这个性质是必须的。
- 单调性: 当激活函数是单调的时候,单层网络能够保证是凸函数。
- 输出值的范围: 当激活函数输出值是有限的时候,基于梯度的优化方法会更加稳定,因为特征的表示受有限权值的影响更显著;当激活函数的输出是无限的时候,模型的训练会更加高效,不过在这种情况少,一般需要更小的learning rate。
常见的激活函数
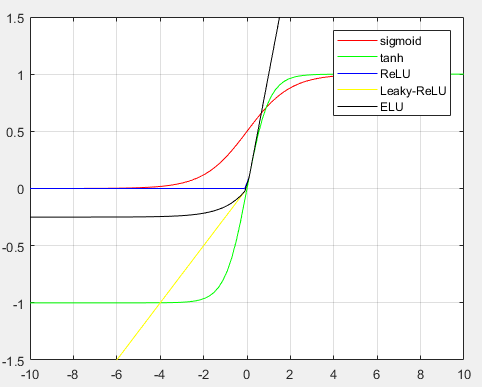
如图,是激活函数的大分类:

目前来讲,选择怎样的激活函数不在于它能否模拟真正的神经元,而在于能否便于优化整个深度神经网络。在分别介绍各种激活函数并进行优劣对比和决策分析之前,先科普一个非常重要的概念——饱和。
饱和
假设$h(x)$是一个激活函数,对于其导数$h'(x)$而言:
- 当$x$趋近于正无穷时,函数的导数趋近于0,我们称其为右饱和;$${\lim_{x \to +\infty}} h'(x)= 0$$
- 当$x$趋近于负无穷时,函数的导数趋近于0,称其为左饱和。$${\lim_{x \to -\infty}} h'(x)= 0$$
若一个函数既满足左饱和又满足右饱和,则该函数为饱和函数,否则为非饱和函数。
典型的饱和激活函数有如Sigmoid和tanh,非饱和激活函数有ReLU。相较于饱和激活函数,非饱和激活函数可以解决“梯度消失”的问题,加快收敛。
硬饱和和软饱和
对于任意的$x$,若存在常数$c$,当$x > c$时,恒有$h'(x) = 0$成立,则称其为右硬饱和。同理,若存在常数$c$,当$x < c$时,恒有$h'(x) = 0$成立,则称其为左硬饱和。当一个函数既满足又硬饱和和左硬饱和,则称该函数为硬饱和。
对于任意的$x$,若存在常数$c$,当$x > c$时,恒有$h'(x) = 0$,则称其为右软饱和。同理,若存在常数$c$,当$x < c$时,恒有$h'(x) = 0$,则称其为左软饱和。当一个函数既满足右软饱和和左软饱和,则称该函数为软饱和。
Sigmoid
Sigmoid函数的一般形式是:$$\sigma(x;a) = \frac{a}{1 + \mathrm{e}^{-ax}}$$
这里,参数$a$控制Sigmoid函数的形状,对函数基本性质没有太大的影响。在神经网络中,一般设置$a = 1$,直接省略。
Sigmoid 函数的导数:$$\sigma'(x) = \sigma(x)(1 + \sigma(x))$$
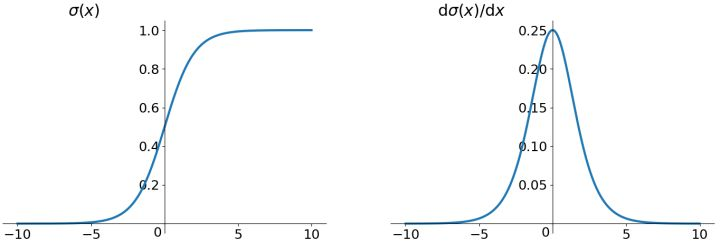
特性:Sigmoid是使用范围最广的一类激活函数,具有指数函数的形状,平滑易于求导,在物理上最接近神经元。它的输出范围为[0, 1],可表示成概率或者用于数据的归一化。
三大缺点
一、梯度消失问题(Gradien Vanishing)
Sigmoid函数在深度网络中常常会导致导数逐渐变为0,使得参数无法被更新,神经网络无法被优化。原因在于两点:
(1)Sigmoid是饱和函数,具有软饱和性。从上图左可以看出,当$\sigma(x)$中$x$较大或较小时,导数接近$0$,而反向传播的数学依据是微积分求导的链式法则,当前层的导数需要之前各层导数的乘积,几个小数的相乘,结果会很接近$0$。同时,对于权重矩阵的初始化,为了防止饱和,也必须特别留意:如果初始化权重过大,可能很多神经元得到一个比较小的梯度,致使神经元不能很好的更新权重提前饱和,神经网络就几乎不学习。
(2)从上图右也可看出Sigmoid的导数都是小于0.25的,这意味着导数在每一层至少会被压缩为原来的1/4,通过两层后被变为1/16,…,通过10层后为1/1048576。那么在进行反向传播的时候,梯度相乘结果会慢慢地趋近于0。这样,几乎就没有梯度信号通过神经元传递到前面层的梯度更新中,使得前面层的权值几乎没有更新,前层网络很难得到有效训练,这类梯度消失跟网络深度有关。
二、输出不是关于原点中心对称的(zero-centered)
关于激活函数不zero-centered所带来的问题,先讲一下三个概念:
收敛速度
模型的最优解即是模型参数的最优解。通过逐轮迭代,模型参数会被更新到接近其最优解。这一过程中,迭代轮次多,则我们说模型收敛速度慢;反之,迭代轮次少,则我们说模型收敛速度快。
参数更新
深度学习一般的学习方法是反向传播。简单来说,就是通过链式法则,求解全局损失函数$L(\vec x)$对某一参数$w$的偏导数(梯度);而后辅以学习率$\eta$,向梯度的反方向更新参数$w$。$$w \gets w - \eta \cdot \frac{\partial L}{\partial w}$$
考虑学习率$\eta$是全局设置的超参数,参数更新的核心步骤即是计算$\frac{\partial L}{\partial w}$。再考虑到对于某个神经元来说,其输入与输出的关系是$$f(\vec x;\vec w, b) = f(z) = f(\sum_{i}w_ix_i + b)$$
因此,对于参数$w_i$来说,$$\frac{L}{w_i] = \frac{\partial L}{\partial f} \frac{\partial f}{\partial z} \frac{\partial z}{\partial w_i} = x_i\cdot \frac{\partial L}{\partial f} \frac{\partial f}{\partial z}$$
因此,参数的更新步骤变为$$w_i \gets w_i - \eta x_i\cdot \frac{\partial L}{\partial f} \frac{\partial f}{\partial z}$$
更新方向
由于$w_i$是上一轮迭代的结果,此处可视为常数,而$\eta$是模型超参数,参数$w_i$的更新方向实际上由$x_i\cdot \frac{\partial L}{\partial f} \frac{\partial f}{\partial z}$决定。
又考虑到$\frac{\partial L}{\partial f} \frac{\partial f}{\partial z}$对于所有的$w_i来说是常数,因此各个$w_i$更新方向之间的差异,完全由对应的输入值$x_i$的符号决定。
至此,为了描述方便,我们以二维的情况为例。亦即,神经元描述为$$f(\vec x;\vec w, b) = f(w_0x_0 + w_1x_1 + b)$$
现在假设,参数$w_0, w_1$的最优解$w_0^*, w_1^*$满足条件$$\left\{ \begin{array}{l} w_0 < w_0^* \\ w_1 \geq w_1^* \end{array}\right.$$
这也就是说,我们希望$w_0$适当增大,但希望$w_1$适当减小。考虑到上一小节提到的更新方向的问题,这就必然要$x_0$和$x_1$符号相反。
但在 Sigmoid 函数中,输出值恒为正。这也就是说,如果上一级神经元采用 Sigmoid 函数作为激活函数,那么我们无法做到$x_0$和$x_1$符号相反。此时,模型为了收敛,不得不向逆风前行的风助力帆船一样,走Z字形逼近最优解。
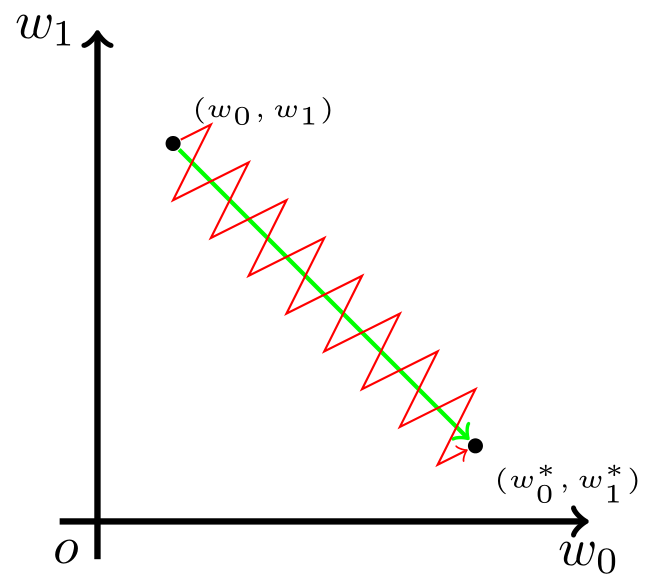
如图,模型参数走绿色箭头能够最快收敛,但由于输入值的符号总是为正,所以模型参数可能走类似红色折线的箭头。如此一来,使用Sigmoid函数作为激活函数的神经网络,收敛速度就会慢上不少了。
三、计算耗时
指数函数的幂运算,计算量大,相对比较消耗计算资源,时间较长。
tanh
tanh 函数全称 Hyperbolic Tangent,即双曲正切函数。它的表达式是$$\tanh(x) = 2\sigma(2x) - 1 = \frac{\mathrm{e}^{x} - \mathrm{e}^{-x}} {\mathrm{e}^{x} + \mathrm{e}^{-x}}$$
双曲正切函数的导数:$$tahn'(x) = 1 - tahn^2(x)$$
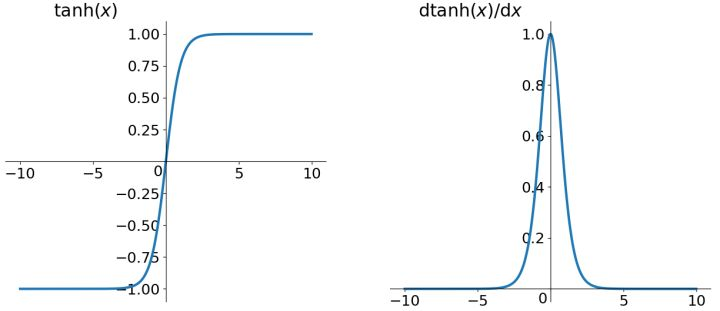
特性:tanh和Sigmoid非常相似,实际上,tanh是Sigmoid的变形:$tanh(x) = 2sigmoid(2x) - 1$。与Sigmoid不同的是,tanh是“零为中心”的。因此,实际应用中,tanh会比Sigmoid更好一些。但是在饱和神经元的情况下,tanh还是没有解决梯度消失问题。
缺点:依然是幂运算,相对耗时;导数值较小(小于1),也具有软饱和性,对梯度消失问题依旧无能为力;
ReLU
ReLU是目前使用最频繁的一个函数,如果你不知道你的激活函数应该选择哪个,那么建议你选择ReLU试试。一般情况下,将ReLU作为你的第一选择。
ReLU全称是Rectified Linear Unit,中文名字:修正线性单元。ReLU是Krizhevsky、Hinton等人在2012年《ImageNet Classification with Deep Convolutional Neural Networks》论文中提出的一种线性且不饱和的激活函数。它的数学表达式为:
$$f(x) = \max(0, x)$$
导数为:$$\begin{align} if&\quad z < 0, \sigma'(x) = 0 \\ if&\quad z \geq 0, \sigma'(x) = 1\end{align}$$
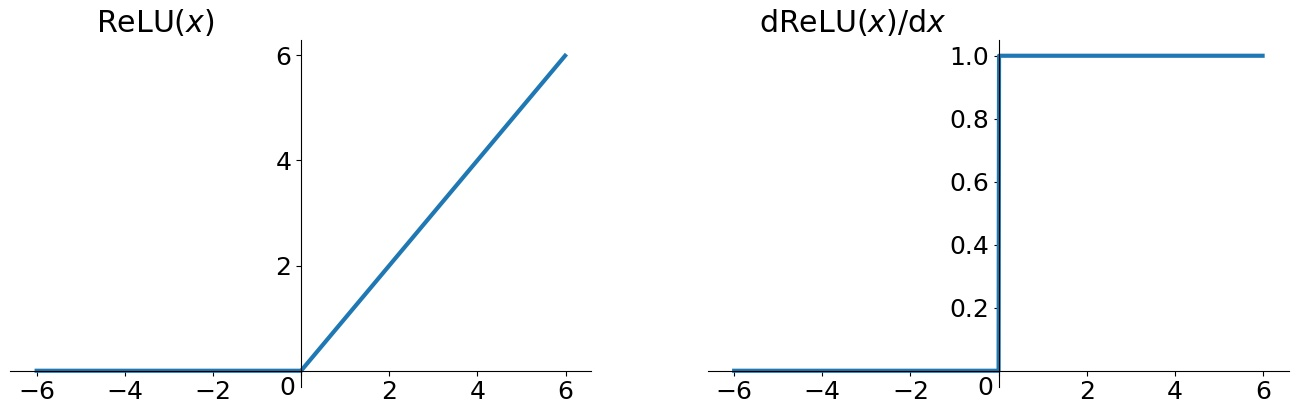
ReLU的优点
(1)ReLU一定程度上缓解了梯度消失的问题,至少$x$在正区间内(x > 0),神经元不会饱和;
(2)由于ReLU线性(正区间)、非饱和的特性,在SGD中能够快速收敛,比Sigmoid与tanh要快很多;
(3)运算速度要快很多。ReLU函数只有线性关系(正区间),不需要指数计算,不管在前向传播还是反向传播,计算速度都比Sigmoid和tanh快。
ReLU的缺点
(1)ReLU的输出不是“零为中心”(Not zero-centered output)。
(2)随着训练的进行,可能会出现神经元“死亡”,权重无法更新的情况,且这种神经元的死亡是不可逆转的死亡。
########################################
这里重点讲一下
Dead ReLU Problem
神经元“死亡”,意味着表示某些神经元可能永远不会被激活, 导致其相应的参数永远不能被更新,其本质是由于Relu在$x < 0$时其梯度为$0$所导致的。
假设有一个神经网络的输入$W$遵循某种分布,对于一组固定的参数(样本),$w$的分布也就是ReLU的输入的分布。假设ReLU输入是一个低方差中心在+0.1的高斯分布。
在这个场景下:
- 大多数ReLU的输入是正数,因此
- 大多数输入经过ReLU函数能得到一个正值(ReLU is open),因此
- 大多数输入能够反向传播通过ReLU得到一个梯度,因此
- ReLU的输入$w$一般都能得到更新(通过随机反向传播SGD)
现在,假设在随机反向传播的过程中,有一个巨大的梯度经过ReLU,由于ReLU是打开的,将会有一个巨大的梯度传给输入$w$。这会引起输入$w$巨大的变化,也就是说输入$w$的分布会发生变化,假设输入$w$的分布现在变成了一个低方差的,中心在-0.1高斯分布。
在这个场景下:
- 大多数ReLU的输入是负数,因此
- 大多数输入经过ReLU函数能得到一个0(ReLU is close),因此
- 大多数输入不能反向传播通过ReLU得到一个梯度,因此
- ReLU的输入$w$一般都得不到更新
发生了什么?只是ReLU函数的输入的分布函数发生了很小的改变(-0.2的改变),导致了ReLU函数行为质的改变。我们越过了0这个边界,ReLU函数就几乎永久的关闭了。更重要的是ReLU函数一旦关闭,参数$w$就得不到更新,这就是所谓的"dying ReLU"。
从数学上说,这是因为ReLU的数学公式导致的$f(x) = \max(x, 0)$,导数:$\nabla_xf(x) = 0(x \leq 0)$。所以可以看出,如果在前向传播的过程中ReLU is close(输出是0),那么反向传播时,ReLU也是close的(梯度是0)。
结论:出现Dead ReLU Problem一般有两种情况:
(1)learning rate太高导致在反向传播的过程中参数更新太大,而大的梯度更新可能会导致参数$W$的分布小于0,当流经过ReLU单元时可能导致神经元不会在以后任何数据节点再被激活,如当进入Relu单元的数都是负数时,Relu将其非线性化成0。当这发生时,经过此神经元的梯度也将永远为0,参数就不会被更新,导致神经元不再学习。也就是说,ReLU单元可能不可逆地在训练中的数据流中关闭(死亡),之后的参数永久不更新将导致训练数据多样化的丢失。
(2)非常不幸的参数初始化,这种情况比较少见 ;
解决方法是可以采用Xavier初始化方法,以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。
########################################
引出的问题:神经网络中ReLU是线性还是非线性函数?为什么relu这种“看似线性”(分段线性)的激活函数所形成的网络,居然能够增加非线性的表达能力?
- ReLU是非线性激活函数。
- 让我们先明白什么是线性网络?如果把线性网络看成一个大的矩阵M。那么输入样本A和B,则会经过同样的线性变换MA,MB(这里A和B经历的线性变换矩阵M是一样的)
- 的确对于单一的样本A,经过由relu激活函数所构成神经网络,其过程确实可以等价是经过了一个线性变换M1,但是对于样本B,在经过同样的网络时,由于每个神经元是否激活(0或者Wx+b)与样本A经过时情形不同了(不同样本),因此B所经历的线性变换M2并不等于M1。因此,ReLU构成的神经网络虽然对每个样本都是线性变换,但是不同样本之间经历的线性变换M并不一样,所以整个样本空间在经过ReLU构成的网络时其实是经历了非线性变换的。
在实际训练中,如果学习率设置的太高,可能会发现网络中40%的神经元都会死掉,且在整个训练集中这些神经元都不会被激活。所以,设置一个合适的较小的学习率,会降低这种情况的发生。而为了解决神经元节点死亡的情况,有人提出了Leaky ReLU、P-ReLu、R-ReLU、ELU等激活函数。
Leaky ReLU
ReLU是将所有的负值设置为0,造成神经元节点死亡情况。相反,Leaky ReLU是给所有负值赋予一个非零的斜率。Leaky ReLU激活函数是在声学模型(2013)中首次提出来的。它的数学表达式为:$$f(x) = \begin{cases} x,&\quad if\quad x > 0 \\ \alpha x,&\quad if\quad x \leq 0\end{cases}$$
导数:$$f'(x) = \begin{cases} 1&\quad x > 0 \\ \alpha&\quad x \leq 0\end{cases}$$

优点:
- 神经元不会出现死亡的情况。
- 对于所有的输入,不管是大于等于0还是小于0,神经元不会饱和。
- 由于Leaky ReLU线性、非饱和的形式,在SGD中能够快速收敛。
- 计算速度要快很多。Leaky ReLU函数只有线性关系,不需要指数计算,不管在前向传播还是反向传播,计算速度都比sigmoid和tanh快。
缺点:Leaky ReLU函数中的参数$\alpha$需要通过先验知识人工赋值。
总结:Leaky ReLU很好的解决了“dead ReLU”的问题。因为Leaky ReLU保留了x小于0时的梯度,在x小于0时,不会出现神经元死亡的问题。对于Leaky ReLU给出了一个很小的负数梯度值$\alpha$,这个值是很小的常数。比如:0.01。这样即修正了数据分布,又保留了一些负轴的值,使得负轴信息不会全部丢失。但是这个$\alpha$通常是通过先验知识人工赋值的。
P-ReLU
Parametric ReLU是基于参数的方法,是对Leaky ReLU的改进:可以自适应地从数据中学习参数。P-ReLU具有收敛速度快、错误率低的特点,可以用于反向传播的训练,可以与其他层同时优化。其数学表达式和导数与Leaky ReLU一样,区别只是参数$\alpha$由back propagation学出来,而并非人工赋值:
$$\Delta a_i = \mu\Delta a_i + \epsilon\frac{\partial \epsilon}{\partial a_i}$$
特性:P-ReLU只增加了极少量的参数,也就意味着网络的计算量以及过拟合的危险性都只增加了一点点。特别的,当不同channels使用相同的$\alpha$时,参数就更少了。
R-ReLU
R-ReLU的英文全称是“Randomized Leaky ReLU”,中文名字叫“随机修正线性单元”,即Leaky ReLU的随机版本。它首次是在Kaggle的NDSB比赛中被提出来的,其图像和表达式如下图所示:
数学表达式:$$y_{ij} = \begin{cases} x_{ij}&\quad if \quad x_{ij} \geq 0 \\ a_{ji}x{ji}&\quad if \quad x_{ji} < 0\end{cases} \\ where\quad a_{ji} \sim U(l, u), l < u\quad and\quad l, u \in [0, 1)$$
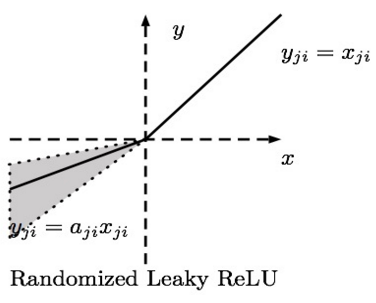
R-ReLU的核心思想是:在训练过程中,$\alpha$是从一个高斯分布$U(l, u)$中随机出来的值,然后再在测试过程中进行修正。在测试阶段,把训练过程中所有的$a_{ij}$取平均值。
特性:(1)RReLU是Leaky ReLU的random版本,在训练过程中,$\alpha$是从一个高斯分布中随机出来的,然后再测试过程中进行修正。(2)数学形式与P-ReLU类似,但R-ReLU是一种非确定性激活函数,其参数是随机的。
ReLU、Leaky ReLU、PReLU和RReLU的比较

总结
(1)P-ReLU中的$\alpha$是根据数据变化的;
(2)Leaky ReLU中的$\alpha$是固定的;
(3)R-ReLU中的$\alpha$是一个在给定范围内随机抽取的值,这个值在测试环节就会固定下来。
ELU
ELU的英文全称是“Exponential Linear Units”,中文全称是“指数线性单元”,是对ReLU激活函数的一种演变。将激活函数更能够保持一个noise-robust状态,所以提出一个具有负值的激活函数,这可以使得平均激活接近于零,从而加快学习速度。同时,它还能通过正值的标识来避免梯度消失的问题。根据一些研究显示,ELU分类精确度是高于ReLU的。
数学表达式为:$$f(x) = \begin{cases} x,& if \quad x > 0\\ \alpha(\mathrm{e}^x - 1),& otherwise\end{cases}$$
导数:$$f'(x) = \begin{cases} 1,& if \quad x > 0\\ f(x) + \alpha,& otherwise\end{cases}$$
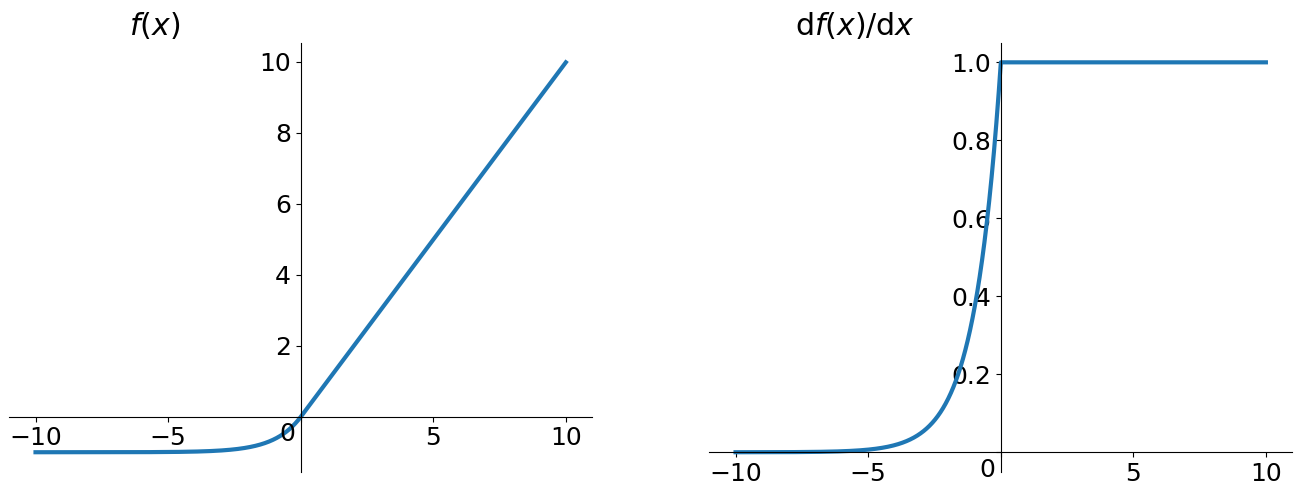
特性:ELU通过在正值区间取输入$x$本身减轻了梯度弥散问题($x > 0$区间导数处处为1),这一点特性这四种激活函数都具备。四者当中只有ReLU的输出值没有负值,所以输出的均值会大于0,当激活值的均值非0时,就会对下一层造成一个bias,如果激活值之间不会相互抵消(即均值非0),会导致下一层的激活神经元有bias shift。如此叠加,神经元越多时,bias shift就会越大。相比ReLU,ELU可以取到负值,这让神经元元激活均值可以更接近0,类似于Batch Normalization的效果但是只需要更低的计算复杂度。虽然Leaky ReLU和P-ReLU都也有负值,但是它们不保证在不激活状态下(就是在输入为负的状态下)对噪声鲁棒。反观ELU在输入取较小值时具有软饱和(左侧软饱和,右侧无饱和,右侧的线性部分可以解决梯度消失问题),左侧的软饱和提升了对输入噪声的鲁棒性。如图所示,其中$\alpha$是一个可调整的参数,它控制着ELU负值部分在何时饱和。
总结:ELU也是为解决ReLU存在的问题而提出,显然,ELU有ReLU的基本所有优点,以及不会有Dead ReLU问题,输出的均值接近0(zero-centered)。但它的一个小问题在于计算量稍大,需要计算指数,计算效率较低。
Maxout
Maxout出现在ICML2013上(论文《Maxout Networks》),是由Goodfellow等人提出的一种很有特点的神经元。它的激活函数、计算的变量、计算方式和普通的神经元完全不同,并有两组权重。先得到两个超平面,再进行最大值计算。激活函数是对ReLU和Leaky ReLU的一般化归纳,没有ReLU函数的缺点,不会出现激活函数饱和神经元死亡的情况。
Maxout可以看作深度学习网络中的一层,如池化层、卷积层,我们可以把Maxout看成是网络的激活函数层,我们假设网络某一层的输入特征向量为:$X = (x_1, x_2, \dots , x_d$,也就是我们输入是$d$个神经元。Maxout隐藏层每个神经元的计算公式如下:$$f_i(x) = \max_{j \in [1, k]}z_{ij}$$
其中,$k$就是Maxout层所需要的参数了,由我们人为设定大小。就像Dropout一样,也有自己的参数$p$(每个神经元dropout概率),Maxout的参数是$k$。公式中$z$的计算公式为:其中$z_{ij} = x^TW_{...ij} + b_{ij}$。
权重$W$是一个大小为$(d, m, k)$三维矩阵,$b$是一个大小为$(m, k)$的二维矩阵,这两个就是我们需要学习的参数。如果我们设定参数$k =1$,那么这个时候,网络就类似于以前我们所学普通的MLP网络。
我们可以这么理解,本来传统的MLP算法在第$i$层到第$i + 1$层,参数只有一组,然而现在我们不这么干了,我们在这一层同时训练$n$组的$w、b$参数,然后选择激活值$z$最大的作为下一层神经元的激活值,这个$\max(z)$函数即充当了激活函数。
假设$W$是2维的,那么我们可以得出公式:$f(x) = \max(w_1^Tx + b_1, w_2^Tx + b_2)$
可以注意到,ReLU和Leaky ReLU都是它的一个变形。Maxout的拟合能力非常强,它可以拟合任意的凸函数。Goodfellow在论文中从数学的角度上也证明了这个结论,只需要2个Maxout节点就可以拟合任意的凸函数,前提是“隐含层”节点的个数足够多。
优点:Maxout具有ReLU的所有优点,线性、不饱和性;同时没有ReLU的一些缺点。如:神经元的死亡。
缺点:从最后的激活函数公式14可以看出,每个神经元将有两组$w$,那么参数就增加了一倍。这就导致了整体参数的数量激增。
Softmax
tanh函数和Sigmoid函数的作用是将输入映射到$(0,1)$区间,从而判断属于某个类别,因此Sigmoid一般用于Logic Regression二分类,比如判断一个数是否大于0就是二分类,只有两个结果:是或否。但是现实中经常遇到更为复杂的分类问题比如MNIST问题,即识别手写数字是0~9中的哪一个,这里的分类就成了10类,就无法用Sigmoid来处理,Softmax就可以大展身手了。
Softmax的函数表达式:$$y = \frac{\mathrm{e}^{a_i}}{\sum_{k = 1}^{C} \mathrm{e}^{a_k}}\quad i \in 1\dots C$$
这样可能并不是很清晰,换一个方式表达:$$y = \frac{\mathrm{e}^{i}}{\sum_{j = 1}^{C} \mathrm{e}^{j}}\quad i \in 1\dots C$$
假设分类结果有$C$种(MNIST中即有10种),$y$代表的就是第$i$种的概率,那么结果会是一个$C$维向量$(y_1, y_2, \dots , y_c)$,其中$y_1$代表该输出是第一类的概率,$y_2$代表该输出是第2类的概率以此类推,然后我们选取其中概率最大的一个作为我们的结果。更通俗理解就是Softmax将输入值映射成属于每个类别的概率,且含有softmax激活函数的网络层有这样一个性质:$\sum_{i = 1}^{j} \sigma_i(z) = 1$。
这里只介绍了Softmax的原理,而在反向传播中要用到Softmax的导数,这个导数的求解看似复杂其实也就是一个高中数学导数题,而这里有篇文章专门来介绍导数的求解,有兴趣的可以去看看:Softmax函数与交叉熵。
Softplus数学表达式:$$f(x) = log(\mathrm{e}^x + 1)$$
Softsign数学表达式:$$f(x) = \frac{1}{|x| + 1}$$
决策原则
目前还不存在定论,在实践过程中更多还是需要结合实际情况,考虑不同激活函数的优缺点综合使用。几点建议。
(1)深度学习往往需要大量时间来处理大量数据,模型的收敛速度是尤为重要的。所以,总体上来讲,训练深度学习网络尽量使用zero-centered数据 (可以经过数据预处理实现) 和zero-centered输出。所以要尽量选择输出具有zero-centered特点的激活函数以加快模型的收敛速度。
(2)通常来说,不能把各种激活函数串起来在一个网络中使用。
(3)如果你不知道应该使用哪个激活函数, 那么请优先选择Relu。
(4)如果使用ReLU,那么一定要小心设置学习率(learning rate),并且要注意不要让网络中出现很多死亡神经元。如果死亡神经元过多的问题不好解决,可以试试Leaky ReLU、PReLU或者Maxout。
(5)除非在二分类问题中,否则请尽量不要使用sigmoid激活函数,可以试试tanh,不过预期效果可能还是比不上ReLU和Maxout。
(整理自网络)
参考资料:
https://www.cnblogs.com/wyshen/archive/2004/01/13/13399578.html
https://www.cnblogs.com/XDU-Lakers/p/10557496.html
https://blog.csdn.net/disiwei1012/article/details/79204243
https://zhuanlan.zhihu.com/p/25110450
https://zhuanlan.zhihu.com/p/44398148
https://zhuanlan.zhihu.com/p/41894523


 浙公网安备 33010602011771号
浙公网安备 33010602011771号