斐波那契数列高效算法之快速幂法、快速倍增法与扩域法
目前网络上介绍斐波那契数列算法的文章数不胜数, 但是高效算法主要围绕矩阵快速幂法展开. 但实际上还有两种算法: 快速倍增法和扩域法, 均能达到 \(O(\log n)\) 的时间复杂度, 在一定程度的优化后甚至能做到更小的常数, 从而拥有更高的效率. 下面介绍三种算法, 同时给出必要的原理与简要推导.
快速幂法
既然要讲快速算法, 首先还是要介绍快速幂法, 因为其是快速倍增法的基础.
快速幂法基于以下递推式:
或可作
这个式子原理比较简单, 网上也有很多推导过程, 故此处不再列出.
基于第二个递推式, 可构造一个无符号整数结构体, 为其实现乘法与快速幂运算, 即可通过求 \(n\) 次方得到 \(F(n)\).
use std::ops::Mul;
#[derive(Copy,Debug, Clone)]
struct Mat2x2(u64, u64, u64, u64);
impl Mul for Mat2x2 {
type Output = Self;
fn mul(self, rhs: Self) -> Self::Output {
Self(
self.0 * rhs.0 + self.1 * rhs.2,
self.0 * rhs.1 + self.1 * rhs.3,
self.2 * rhs.0 + self.3 * rhs.2,
self.2 * rhs.1 + self.3 * rhs.3,
)
}
}
impl Mat2x2 {
fn pow(mut self, mut exp: u64) -> Self {
let mut ans = Self(1, 0, 0, 1);
while exp > 0 {
if exp & 1 == 1 {
ans = ans * self;
}
self = self * self;
exp >>= 1;
}
ans
}
}
fn fib(n: u64) -> u64 {
let ori = Mat2x2(0, 1, 1, 1);
ori.pow(n).1
}
由快速幂原理可得, 时间复杂度取决于 pow 函数中指数的二进制位数, 故时间复杂度为 \(O(\log n)\); 使用的空间为常数, 故空间复杂度为 \(O(1)\).
快速倍增法
通过矩阵幂可推导出以下基础公式:
通过矩阵乘法公式计算 \(F(2n)\) 和 \(F(2n+1)\) 项即可得到快速倍增法公式.
同时也可写作以下变体形式, 与基础公式等价, 但在 \(F(2)\) 处存在无限递归, 后续推导会用到.
基于快速倍增法基础公式可以得到如下代码:
fn fib(n: u64) -> u64 {
match n {
0 => 0,
1 => 1,
n if n % 2 == 0 => {
let n = n / 2;
fib(n) * (fib(n) + 2 * fib(n - 1))
}
n if n % 2 == 1 => {
let n = n / 2;
fib(n).pow(2) + fib(n + 1).pow(2)
}
_ => unreachable!(),
}
}
可以看到目前的方案有两个问题
- 计算存在重复, 比如需要求 \(F(6)\) 就要计算 \(F(3)\), \(F(2)\), 计算 \(F(3)\) 时又会再次计算 \(F(2)\), 当计算项变多时重复项也会越来越多;
- 计算过程是递归的, 而且不是尾递归, 可能导致性能下降.
首先解决重复计算问题, 通常解决这类问题可以采用记忆化搜索方法, 将计算的中间值用数组保存起来, 当需要用到时就直接用, 不必重复计算. 但对于快速倍增法有更好的方法, 利用变体形式, 我们每次计算 \(F(2n)\) 和 \(F(2n+1)\) 两项就可以避免重复. 以 \((F(12), F(13))\) 计算为例进行演示:
根据变体公式, 求 \((F(12), F(13))\) 需要求 \((F(6), F(7))\), 进而需要求 \((F(3), F(4))\), 但 \((F(3), F(4))\) 不满足 \((F(2n), F(2n+1))\) 形式, 利用 \(F(4) = F(3) + F(2)\) 改为求 \((F(2), F(3))\), 最后一步步到 \((F(0), F(1))\).
求解的过程满足下表:
| 2n | bin(2n) | F(2n), F(2n+1) | 满足形式 | 变换形式 |
|---|---|---|---|---|
| 12 | 1100 | F(12), F(13) | true | - |
| 6 | 110 | F(6), F(7) | true | - |
| 3->2 | 11 | F(3),F(4) | false | F(2),F(3) |
| 1->0 | 1 | F(1),F(2) | false | F(0), F(1) |
可以发现当二进制最低位为1时(奇数), 形式将不满足条件, 需要向下一级变换形式.
基于以上逻辑, 引入 fib_pair 辅助函数, 输入 \(n\), 输出 \((F(n), F(n+1))\) 对:
fn fib_pair(n: u64) -> (u64, u64) {
match n {
0 => (0, 1),
n => {
let (l, h) = fib_pair(n / 2); // low and high
let a = l * (2 * h - l);
let b = l * l + h * h;
if n % 2 == 0 { (a, b) } else { (b, a + b) }
}
}
}
fn fib(n: u64) -> u64 {
fib_pair(n).0
}
接下来消除递归过程, 在前文中你可能已经注意到快速倍增法与项的奇偶性密切相关, 这里通过将通过二进制按位分解来将递归化为迭代.
我们将之前的二进制表翻转, 改为从 \((F(0), F(1))\) 向上求值, 判断输入二进制的最高位到最低位, 当前位为0则用
用 \(F(n)\), \(F(n+1)\) 求 \(F(2n)\), \(F(2n+1)\), 当前位为1则用 \(F(n+2) = F(n)+F(n+1)\) 上一级变换形式
| bin(n) | F(n), F(n+1) | bin(n)最高位不为1 | 变换形式 |
|---|---|---|---|
| 1100 | F(0),F(1) | false | F(1),F(2) |
| 100 | F(2),F(3) | false | F(3),F(4) |
| 00 | F(6), F(7) | true | - |
| 0 | F(12),F(13) | true | - |
可以看到该过程恰好就是递归方案的逆过程, 而且该方案无需递归
fn fib_pair(n: u64) -> (u64, u64) {
if n == 0 {
(0, 1)
} else {
let (mut l, mut h) = (0u64, 1u64);
let bit_length = n.ilog2();
let mut mask = 1 << bit_length;
while mask != 0 {
(l, h) = (l * (2 * h - l), l * l + h * h);
if n & mask != 0 {
(l, h) = (h, l + h);
}
mask >>= 1;
}
(l, h)
}
}
fn fib(n: u64) -> u64 {
fib_pair(n).0
}
其中mask最高位与n的最高位一致, 其余全是0, 通过 n & mask; mask >>= 1; 就能从高到低遍历n的每一位. 从而无递归地利用快速倍增法求斐波那契数.
扩域法
接下来是比较少被人提到的方法: 扩域法.
首先我们看一下斐波那契数列的通项公式:
利用这个公式理论结合浮点数快速幂能够在 \(O(\log n)\) 时间内求解, 但是浮点数运算存在精度问题, 当 \(n\) 较大时很快就会精度不足.
但注意运算过程中只存在 \(\sqrt{5}\) 这唯一一个无理数, 所有数字均可表示为 \(a+b\sqrt{5}, a,b\in Q\) 形式. 如果能通过某个方法, 在运算过程中消除这个无理数, 或者用某个数据结构代替这个无理数, 就有可能避免浮点运算.
在中学阶段, 学习到复数时, 我们通过引入 \(i\) 和数对 \((a,b)\) 让复数 \(a+bi\) 运算能够用实数计算. 仿照复数的这种构造方式, 令
模仿虚数的实部虚部的称呼, 本文将 \(a\) 称为有理部, \(b\) 为无理部系数.
定义取有理部和无理部系数函数:
通过简单推算得到其四则运算的公式
可以发现计算结果仍满足 \((a,b)\) 结构, 在数学上这构成了一个 \(Q(\sqrt{5})\) 数域, 所以这个方法称为扩域法.
使用这个方法可以将斐波那契数列公式改写为
但这个公式目前仍不能完全消除浮点数的存在, 因为在其中还存在以下几个非整数项
但是可以发现, 第一项 \(1/(0,1)\) 乘以后续结果的作用就是将后续结果的无理部系数提取出来, 所以可以通过以下公式避免第一项的计算
对于 \((1,1)/2\) 等导致的浮点数, 我们可以将除法放到最后计算, 得到公式
到此我们成功消除了所有浮点数的存在, 可以得到初步的代码
use std::ops::{Div, Mul, Sub};
#[derive(Clone, Copy)]
pub struct QSqrt5(i64, i64);
impl Mul for QSqrt5 {
type Output = Self;
fn mul(self, rhs: Self) -> Self::Output {
Self(
self.0 * rhs.0 + 5 * self.1 * rhs.1,
self.0 * rhs.1 + self.1 * rhs.0,
)
}
}
impl Sub for QSqrt5 {
type Output = Self;
fn sub(self, rhs: Self) -> Self::Output {
Self(self.0 - rhs.0, self.1 - rhs.1)
}
}
impl Div<i64> for QSqrt5 {
type Output = Self;
fn div(self, rhs: i64) -> Self::Output {
Self(self.0 / rhs, self.1 / rhs)
}
}
impl QSqrt5 {
fn pow(mut self, mut exp: u64) -> Self {
let mut ans = QSqrt5(1, 0);
while exp > 0 {
if exp & 1 == 1 {
ans = ans * self;
}
self = self * self;
exp >>= 1;
}
ans
}
}
fn fib(n: u64) -> u64 {
(QSqrt5(1, 1).pow(n) - QSqrt5(1, -1).pow(n)).1 as u64 >> n
}
以上已经能够得到斐波那契数列了, 且时间复杂度为两次快速幂的指数二进制位数, 同样为 \(O(\log n)\), 使用了常数空间, 故空间复杂度为 \(O(1)\).
扩域法优化
通过之前的优化我们成功消除了公式法中所有无理数和小数, 但存在两个问题:
- 能否消除其中的负数计算, 只保留无符号整数
- 最后整体除 \(2^n\) 说明计算中存在大量因子没有消除, 中间项很大可能导致溢出 (虽然在模 \(2^n\) 数域中这基本不成问题)
通过推导我们发现
所以只需要计算其中任意一个就能得到另一个, 这样就可以不必计算无理部系数为负数的项, 得到新公式
这样就可以直接用无符号整数计算.
在求快速幂时, 计算中间值的同时将 \(2\) 及时约去可以避免溢出, 注意到初始项的 \((1,1)\) 不能被 \(2\) 整除, 所以我们将累乘结果 ans 的初始值设为 \((2, 0)\) 而非 \((1,0)\), 相当于 \(2Ir[(1,1)^n]/2^n\) 分子上的 \(2\), 不将其提前约去来保证每一项都能被 \(2\) 整除.
至此我们得到最终版的扩域法代码
use std::ops::{Div, Mul};
#[derive(Clone, Copy, Debug)]
struct QSqrt5(u64, u64);
impl Mul for QSqrt5 {
type Output = Self;
fn mul(self, rhs: Self) -> Self::Output {
Self(
self.0 * rhs.0 + 5 * self.1 * rhs.1,
self.0 * rhs.1 + self.1 * rhs.0,
)
}
}
impl Div<u64> for QSqrt5 {
type Output = Self;
fn div(self, rhs: u64) -> Self::Output {
Self(self.0 / rhs, self.1 / rhs)
}
}
impl QSqrt5 {
fn pow_div_2(mut self, mut exp: u64) -> Self {
let mut ans = QSqrt5(2, 0);
while exp != 0 {
if exp & 1 == 1 {
ans = ans * self / 2;
}
self = self * self / 2;
exp >>= 1;
}
ans
}
}
fn fib(n: u64) -> u64 {
QSqrt5(1, 1).pow_div_2(n).1
}
这个方法的时间复杂度仍为 \(O(\log n)\), 空间复杂度仍为 \(O(1)\), 但常数较小.
总结
以上三个方法都能实现时间复杂度在 \(O(\log n)\)的条件下求第 \(n\) 项斐波那契数. 通过充分的优化, 三种方法耗时最终, 在个人电脑的 rust 的 release 模式下重复 \(2\times10^{12}\) 计算 F(92) (不超过u64的最大值), 耗时如下.
| method | F(92)time |
|---|---|
| 矩阵快速幂 | 26.558 |
| 快速倍增法 | 17.667 |
| 扩域法 | 22.429 |
可以看出, 快速倍增法 > 扩域法 > 矩阵快速幂法, 性能比最大提升约 30%.
统计 \(F(0)\) 到 \(F(92)\) 的用时并对 \(n\) 作图, 曲线符合 \(O(\log n)\) 的趋势, 有意思的是快速倍增法每当遇到2的幂次时耗时以台阶形式上升.
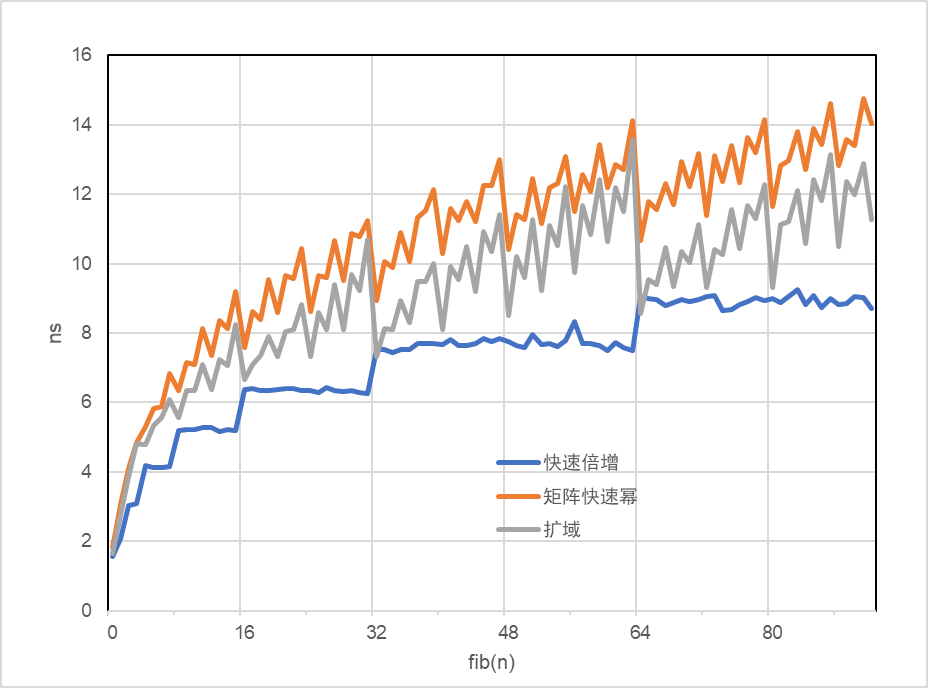
综上, 快速倍增法不论是代码长度, 编程难度和运行效率, 都显著优于另外两个办法, 所以在日常使用时推荐使用快速倍增法.
本文来自博客园,作者:Meth_nylon,转载请注明原文链接:https://www.cnblogs.com/Meth-nylon/p/18869305



 浙公网安备 33010602011771号
浙公网安备 33010602011771号