机器学习的总结

机器学习

序言

是的，我看完d2l了，现在在看西瓜书，感觉西瓜书是d2l的理论基础，遂来写机器学习的笔记，希望对我的dl有帮助，个人水平和理解力有限，不喜勿喷，谢谢！

基本概念

基本概念其实还是很简单的，起码是好理解的。
1.数据集(data set)：一堆数据的集合，里面的每一个数据就是一个样本(sample)，样本是有特征(feature)的，样本构成一个空间(space)，一个样本可能有多个特征，我们用维度(dimensionality)来描述，所以，每一个示例就构成了一个在n维样本空间(sample space)里的特征向量(feature vector)。
2.从数据中学习得到模型的过程成为学习(learning)或者训练(training)，对应的，有训练数据(training data)和训练样本(traininig sample)，使用的成为学习器(learner)来发掘数据的潜在规律，然后进行预测。
3.得到模型之后，是用另一组被称为测试集(test set)的数据集来测试得到我们需要的预测，测试集里的就是测试数据(test data)。
4.泛化(gengralization)，是指模型需要有适应普遍数据的能力，一般来说，泛化能力过差会导致模型过拟合(overfitting)，这也是我们需要优化的一个很重要的点。
5.归纳偏好(inductive bias)：个人理解就是进行一个拟合的过程，前文提到的过拟合，就是在归纳偏好的过程中，将训练数据的点拟合的过于详细，以至于只能适应这个数据集，而无法进行测试。

模型评估和选择

1.过拟合：前文提及
2.欠拟合(underfitting)：就是对训练样本尚未学好。
但问题是我们只有一个大的数据集D，我们应该如何在这个D中分割出测试集和训练集呢？

留出法

留出法，顾名思义，将D分为两个互斥的集合，一个是训练集，一个是测试集，两个集合要是互斥的，注意在分层采样的时候，使用留出法要针对每一层进行分类。朴素但是不稳定

交叉验证法

先将D分为k个大小相似的互斥子集，每个子集都是尽可能保持一致性，然后每次用k-1个子集的并集作为训练集，1个作为测试集，不难发现可以进行k次实验，所以就叫k折交叉验证。稳定，训练充分，但是时间和数据的成本高。

自助法

基于有放回的随机取样的方法，每次从D中随机挑选一个样本放入训练集，对于m次后，不难发现，概率是\(\lim_{n\rightarrow\infty}(1-\frac{1}{m})^m=\frac{1}{e}\)，在数据集较小，难以有效划分集合的时候很好用。

性能度量

正如前文所说，我们需要对模型进行评估，于是就要定义函数来进行评估。
1.均方误差：\(E(f:D)=\frac{1}{m}\sum^{m}_{i=1}(f(x_i)-y_i)^2\)
针对连续的变量，我们还有：\(E(f:D)= \int_{x~D} (f(x_i)-y_i)^2 p(x) \, dx \)

错误率和精度

1.错误率：\(E(f;D)=\frac{1}{m}\sum_{i=1}^{m}II(f(x_i)≠y_i)\)
描述了分类错误的样本占总样本的比例。
2.精度：\(acc(f;D)=\frac{1}{m}\sum_{i=1}^{m}II(f(x_i)=y_i)=1-E(f;D)\)
描述了分类正确的样本占总样本的比例。
当然还有连续的形式，不写了。

查准率，查全率和F1

1.查准率：预测为正例的样本中，真的是正确的样本的占比。
2.查全率：正例中被正确找出来的样本的比例。
3.TP：真正例。
4.FP：假正例。
5.FN：假反例。
6.TN：真反例。
7.查准率：\(\frac{TP}{TP+FP}\)
8.查全率：\(\frac{TP}{TP+FN}\)
二者的增长趋势往往相反。
P-R曲线：

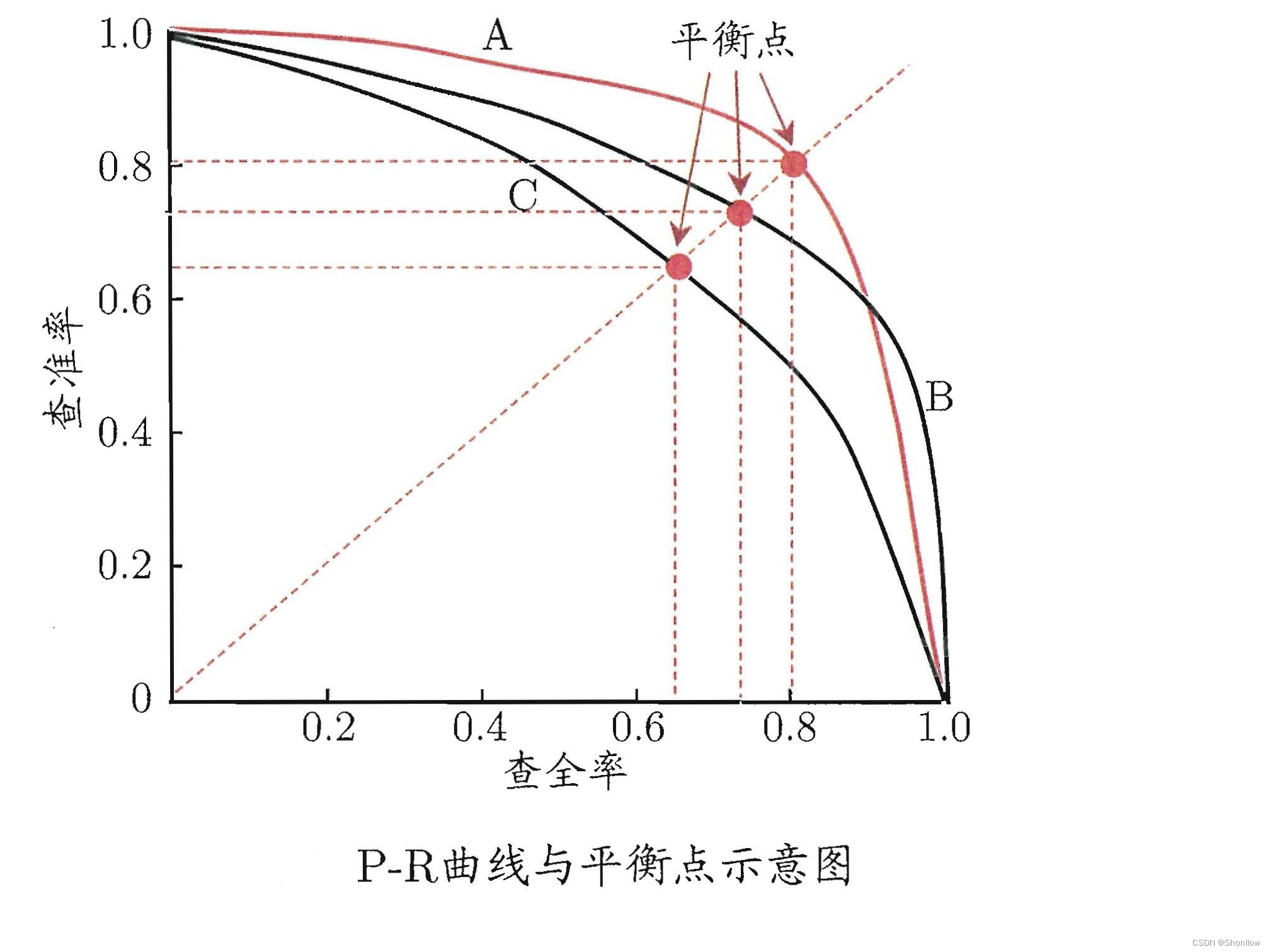
这是一个P-R曲线，如果一条曲线A能够完全包住另一条曲线B，则A的学习性能好于B，如果有交点的时候比较围成的面积即可。
9.平衡点(breaking-point)：基于平衡点的比较，认为A优于B。
10.F-1：\(F-1=\frac{2\times P\times R}{P+R}=\frac{2\times TP}{sum+TP-TN}\)
评估模型表现的。
11.F-β：\(F-β=\frac{(1+β^2)\times P\times R}{(β^2\times P)+R}\)
在β=1的时候是F-1，小于1的时候查准率影响更大，大于1的时候查全率影响更大。
12.macro-F-1：macro-F-1=\(\frac{2\times macro-P\times macro-R}{macro-P+macro-R}\)
是各类别的F-1的算术平均，可以评估一个多分类。
13.micro-F-1：micro-F-1=\(\frac{2\times micor-P\times micro-R}{micro-P+micro-R}\)
评估的是全局的F-1。
14.TPR：TPR=\(\frac{TP}{TP+FN}\)
ROC的纵轴
15.FPR：FPR=\(\frac{FP}{TN+FP}\)
ROC的横轴
16.受试者工作特征(receiver operating characteristic ROC)：由TPR和NPR构成的图像，反应了区分样本正负的能力，越向左上越好。
同P-R曲线，能包住别人的曲线更好，有交叉的时候比较面积，即AUC。
17.AUC(area under ROC curve)：AUC=\(\frac{1}{2}\sum^{i=1}_{m-1}(x_{i+1}-x_i)·(y_i+y{i+1})\)
AUC=1，完美区分，也就是最左上角。
18.损失函数：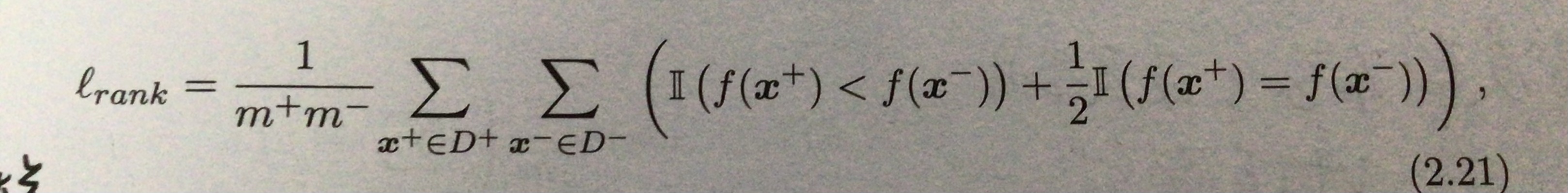
不难看出，loss描述的是ROC上的面积，所以AUC=1-loss。
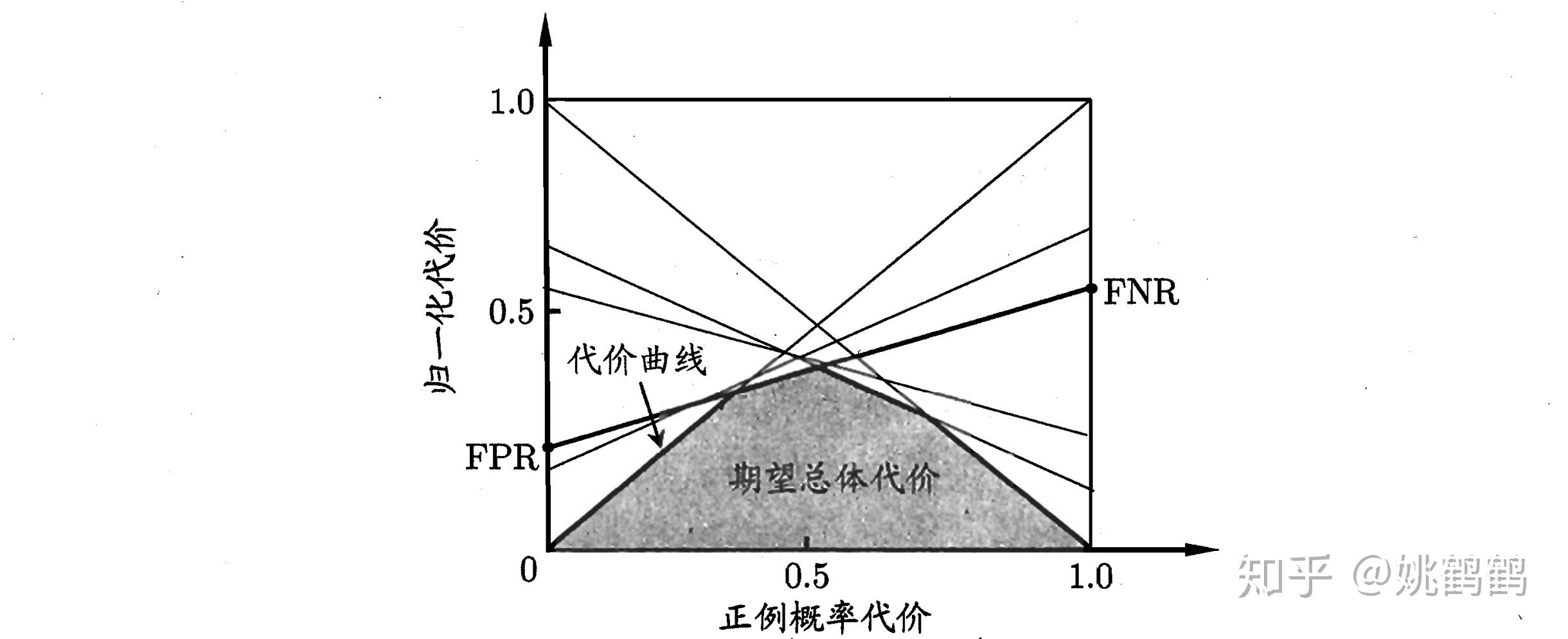
19.代价敏感错误：就是针对不同的问题的选项有不同的权重。这里有一个错误率的概率，错误率是说不区分正负例，来进行评估整体的。有一个公式：$cost_{norm}=\frac{FNR\times p\times cost_{01}+FPR\times (1-p)\times cost_{10}}{p\times_{01}+(1-p)\times cost_{10}}

比较检验

这部分就跟概率论里讲的很相似了。
假设检验，二项检验，交叉验证t检验，McNemar检验，Friedman检验和Nemenyi后续检验。
前两者很像啊，就是二项定理的感觉。
第三个是基于我们之前说过的交叉验证法。
第四个是卡方分布。
第五个是考虑算法的显著性的，最后一个使用置信度来考虑。

偏差与方差

方差很熟悉了，偏差是指期望输出与真是标记的差别，又有一个公式，泛化误差：
\(E(f;D)=bias^2(x)+var(x)+\epsilon^2\)

线性模型