正则化

看书没看懂,汗...
看csdn看懂了

正则化

什么是正则化,就是对于一个损失函数,我们加上一点限制,使得他在之后的函数中,不要过度膨胀.
引入正则化的原因就是前面说过的过拟合和欠拟合,我们当时说的解决过拟合的方法有:
1.清洗数据
2.减少模型参数
3.增加惩罚因子(正则化)

怎么正则化

线性回归

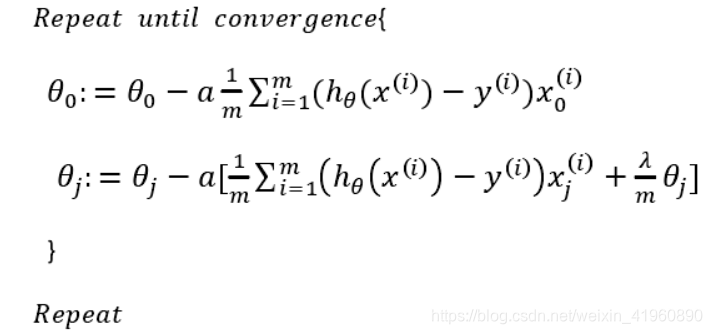
逻辑回归

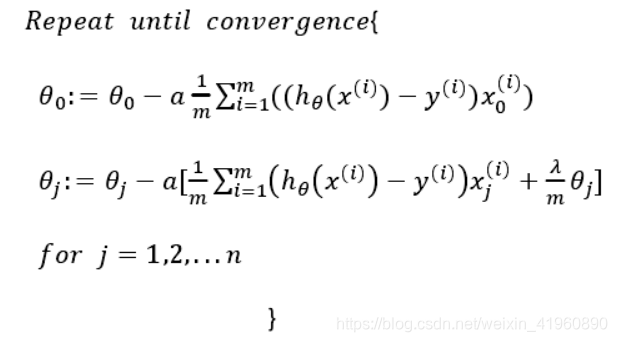
其中的λ是正则化参数,当参数越大,则对其惩罚(规范)的力度也就越大,越能起到规范的作用.
二次正则的优势,处处可导.
L1范数和L2范数:
L1范数:向量中各个元素绝对值之和.
L2范数:欧几里得距离

L1正则

L1正则化的作用是使得大部分模型参数的值等于0,这样一来,当模型训练好后,这些权值等于0的特征可以省去,从而达到稀疏化的目的,节省了存储的空间,因为在计算时,值为0的特征都可以不用存储了.
公式:
\(min_{w}(L(w)+t||w||_1)\)
L1正则化对于所有权重予以同样的惩罚,也就是说,不管模型参数的大小,对它们都施加同等力度的惩罚,因此,较小的权重在被惩罚后,就会变成0.因此,在经过L1正则化后,大量模型参数的值变为0或趋近于0,当然也有一部分参数的值飙得很高.由于大量模型参数变为0,这些参数就不会出现在最终的模型中,因此达到了稀疏化的作用,这也说明了L1正则化自带特征选择的功能,这一点十分有用.

L2正则

\(min_{w}(L(w)+t||w||_2)\)
L2正则化对于绝对值较大的权重予以很重的惩罚,对于绝对值很小的权重予以非常非常小的惩罚,当权重绝对值趋近于0时,基本不惩罚.这个性质与L2的平方项有关系,即越大的数,其平方越大,越小的数,比如小于1的数,其平方反而越小.
在使用正规方程时,解析式中的逆始终存在的.

Dropout

训练时随机丢弃部分神经元输出,等价于对网络结构的随机约束.