学习率与步长

步长

步长是指卷积核(或池化窗口)在输入数据的宽度和高度方向上每次滑动的像素数(对于二维数据，如图像).通常用整数表示,例如步长为 1,2 等.


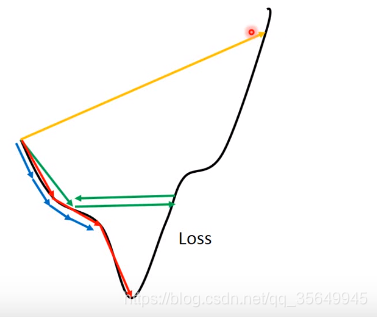
比如我们给出这两个图像
对于一个收敛的过程,总归是要走的,已经到了最低点后,对于这个点的均方误差就是0了,所以在这之后我们无论怎么走,loss一定会增加,然后再接下来的某一步中,会再次接近最低点,所以就会一直波动,带来的影响就是:
步长大->方差大->波动大(不要忘记了loss函数在这一步的时候他的形状?已经固定好了,因为数据已经处理完了,拟合曲线和原点的标准差都计算完成了)

学习率

学习率

学习率决定了在每步参数更新中,模型参数有多大程度(或多大,多长)的调整,并且由一个常数变为了一个超参数(在开始学习之前设置的参数)

参数与超参数

参数:模型中可以被调整和学习的参数,在训练数据的过程中自动学习,来最小化损失函数和优化目标,比如,网络中的权重以及偏差,使用反向传播算法进行训练,目的是找到最佳的参数配置,从而对接下来的模型进行预测.
超参数:在算法运行前手动设置的参数,用于控制模型的行为和性能,会影响训练速度,收敛性,容量和泛化能力,通常是一个试错的过程.

学习率的影响

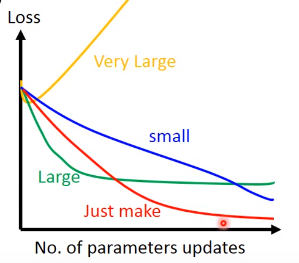
要在收敛和过火间权衡,太小,收敛的慢,太大,损失会震荡

如何调整或者设置

1.先设置一个初始值,可以让损失尽可能快的降低
2.然后设置过程来降低学习率,或者根据实际训练情况,自适应的调整学习率
3.需要对学习率进行热身,因为参数一开始是完全随机的,需要适应

初始化

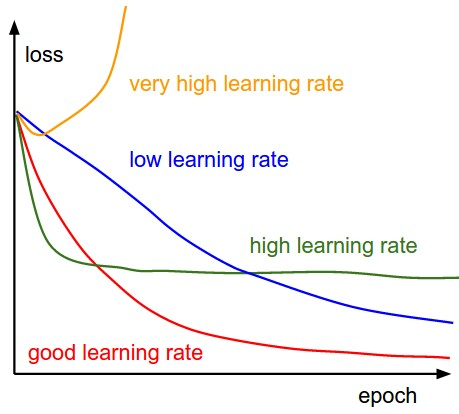
1.以学习率为自变量,在定义域内,随着训练步数增加,学习率从小到大增加
2.画出损失或者准确率随学习率变化的曲线
3.如果是损失变化曲线,选择损失下降最快的学习率作为初始学习率.如果是准确率变化曲线,当精确度增长开始变平或者锯齿状抖动时,就是最大的学习率.

对于第三条的解释

梯度下降的动态平衡:
1.梯度下降能沿着损失函数曲面的负梯度方向稳步逼近最小值,精确度持续提升,损失函数平滑下降.
2.此时,参数更新方向与梯度方向一致,每一步都能有效降低损失.

如何确定最大学习率

有效区间:学习率较小时,精确度随学习率增大而提升,损失函数平滑下降.
临界区间:当学习率超过某个阈值后,精确度增长放缓(放平)或因震荡出现抖动,此时即为最大可行学习率的临界点.

判断标准

变平:精确度长时间不再提升,损失函数趋于稳定但未收敛,说明学习率已无法有效驱动优化.
锯齿状抖动:loss函数呈现波浪形,表明目前在目标解附近震荡,学习率要减小.

准备

warm up:在训练开始前先选者使用一个较小的学习率,在训练了一些步之后再修改为预先设置的学习率(一开始的时候如果学习率较大,可能会带来不稳定)
常量热身与渐进热身:前者训练误差可能会突然增大,后者则比较稳定.

学习率的调整

在训练的过程中,根据训练的火候,设当增加或者减少学习率,使得能够尽快收敛到较优值.大多数情况下都是减少学习率.
方法:
1.学习率Schedule
2.自适应学习率

学习率Schedule

Time-Based公式:
\(\eta_{n+1}=\frac{\eta_n}{1+dn}\)
其中η是学习率,d是衰减超参数,n是训练步骤.
依赖的是上一步的学习率.
Step_Based公式:
\(\eta_n=\eta_0d^{floor(\frac{1+n}{r})}\)
d是衰减因子,r是多少步减少一次学习率.
Exponential公式:
\(\eta_n=\eta_0e^{-dn}\)

自适应学习率

不必设置超参数.模型的数据集上的表现可以被学习算法监控,然后学习算法做出相应调整,这就叫做自适应学习率.这种方法中,学习率会根据损失函数的梯度而增加或减少.如果梯度大,学习率会减少;如果梯度小,学习率会增加.

WarmRestart

每隔若干步就会重启学习率,然后再照常衰减:

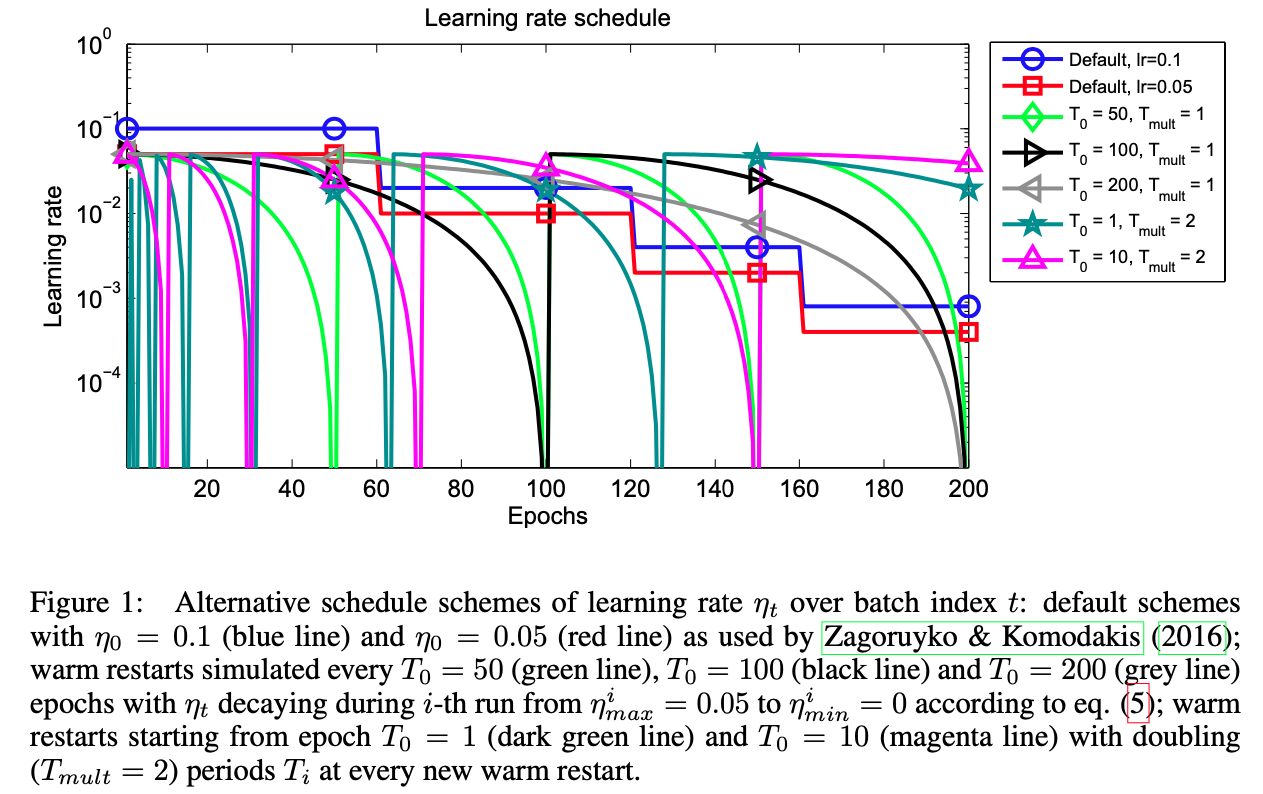
Cycling Learning Rate

Cycling不需要设置初始学习率,也不需要选择衰减schedule和自适应.Cycling设置一个学习率范围,让学习率从最小增加到最大,再从最大减少到最小,循环往复.

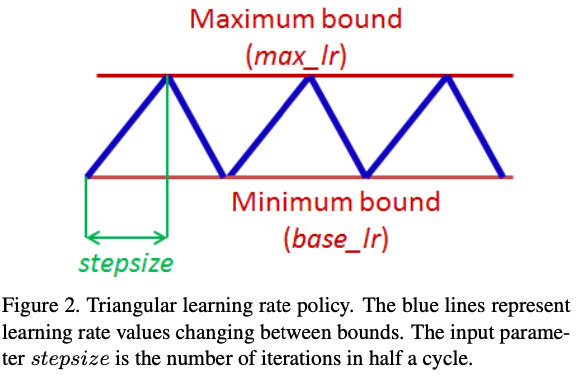
调整学习率的方法

\(\alpha=\frac{\alpha_0}{1+\beta * \lambda}\)
\(\alpha=0.95^{\lambda}*\alpha_0\)
\(\alpha=\frac{k}{\sqrt{\lambda}}\alpha_0\)
\(\alpha=\frac{k}{\sqrt{mini-batch-size}}\)