numpy数组的轴和“约减”(聚合)

numpy数组的轴和“约减”(聚合)

一、轴(axis)

  • 如同笛卡尔坐标系一样，NumPy张量也有轴。现在我们先以熟悉二维向量为例来说明这个概念，二维向量的轴是沿行和列的方向

  • 轴的编号是从0开始的，因此“第一轴”实际上是“axis 0”。“第二轴”是“axis 1”，依此类推。在可视化观感上，“axis 0”就是向下的行方向轴，“axis 1”是沿着水平方向的列轴，如下图所示

  • 以维度为(3,4,5)的三维数组为例：它有3个维度，因此，它的轴有3个，即：“轴0”、“轴1”、“轴2”。

  • 从轴0上看，该数组包含3个元素，进入到轴0中的任何1个元素的空间中，可以看到，这个元素又包含两个轴，对应于三维数组的轴1和轴2

二、数组基于轴的“约减”（聚合）操作

  • 它表示将众多数据按照某种规则合并成一个或几个数据。“约减”之后，数据的个数在总量是减少的。

  • numpy中常用的”约减“方法有7种，不指定轴则默认求的是整个数组，注意：中值和极值这两个方法是numpy开头：

    • ndarray.sum(axis=None)，求和
    • ndarray.mean(axis=None)，求平均值
    • numpy.median(ndarray,axis=None)，求中值（中位数）
    • ndarray.max(axis=None)，最大值
    • ndarray.min(axis=None)，最小值
    • numpy.ptp(ndarray,axis=None)，极值（最大值和最小值之差）
    • ndarray.std(axis=None)，标准差（反应一组数据离平均值的分散程度，值越大说明波动越大，越不稳定）

  • 在这里，“约减”的“减”，并非减法之意，而是向量元素的减少。比如说，数组的加法操作，实际上就是一种“约减”操作，因为它对数组中的众多元素按照某些运算，最后合并为少数的一个或几个值。示例代码如下

 In [1]:import numpy as np 
 In [2]: a = np.ones((2,3))  #创建形状为2×3，元素值均为1的矩阵
 In [3]: a  #显示该矩阵
 Out[3]: 
 array([[1., 1., 1.],
  [1., 1., 1.]])
 In [4]: a.sum() #将6个矩阵元素求和后变成一个元素
 Out[4]: 6.0

  • 我们可以推而广之，求N维数组的均值（mean）、最大值（max）和最小值（min）等，这些操作都属于约减操作

  • 但有时，我们会有这样的需求，对指定维度方向的值进行统计，如统计某一行（或列）的和、均值、最大值、最小值等。这个时候，就需要给“约减”指令指定方向

  • sum（求和）、min（最小值）、max（最大值），mean（均值）、median（中位数）等统计函数，它们都有一个名为操作轴（axis）的参数，其默认值为None，也就是不指定约减方向，它将所有数据都“约减”为一个元素

  • 拿np.sum()方法来说，如果axis的值为0，可简单地理解为从垂直轴方向进行“约减”。如果axis的值为1，则可以简单理解为从水平轴方向进行“约减”

    •  In [3]: a  #显示该矩阵
 Out[3]: 
 array([[1., 1., 1.],
  [1., 1., 1.]])
 In [5]: a.sum(axis = 0) #垂直方向约减
 Out[5]: array([2., 2., 2.])
 In [6]: a.sum(1) #垂直方向约减
 Out[6]: array([3., 3.])
  
"""
在In [5]处，我们使用关键字参数axis = 0，显式给出了约减轴的方向为垂直方向，而在In [6]处，仅仅给出整数值1，它等同于axis = 1，即在水平方向约减，“axis=”做了省略
"""

    • 如下图所示

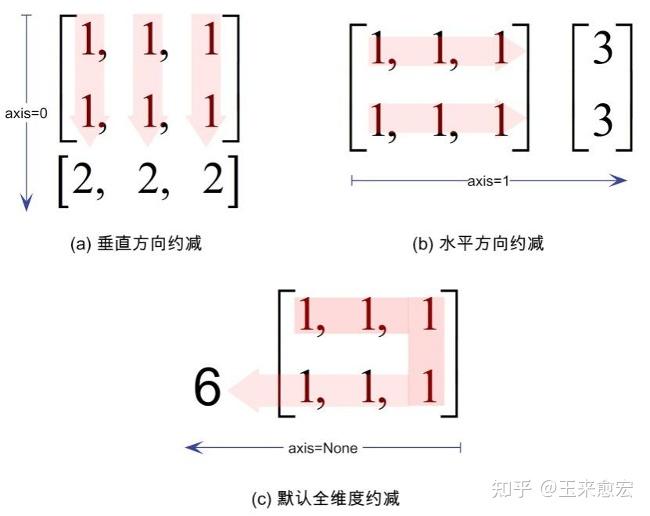
三、三维及以上数组的“约减”分析

  • 二中的图的解释虽然直观，但也有很大的局限性。这是因为，这种可视化轴的概念在维度不超过2时比较容易理解，而且轴0表示垂直方向，轴1表示水平方向，是人为强加的。当维度>=3时，我们难以找到可直观理解的方向

  • 所以，更加普适的解释，应该是按张量括号层次的方式来理解。张量括号由外到内，对应从小到大的维数。比如，对于一个三维的数组 [[[1, 1, 1], [2, 2, 2]], [[3, 3, 3],[4, 4, 4]]] ，它有三层括号，其轴序由外到内分别为 0,1,2

  • axis参数决定聚合哪个轴的数据。聚合意味着这个轴将坍缩（折叠），之所以会坍缩，就是因为执行了“约减”操作

  • 下面以 np.sum 为例

1. 当axis = 0时

  • axis = 0，就是在第0个维度的元素之间进行求和操作，即拆掉最外层括号后（即相当于这个轴坍缩了），对应有2个最大“颗粒度”的元素 [[1, 1, 1], [2, 2, 2]] 和 [[3, 3, 3], [4, 4, 4]] ，这两个元素都是二维数组，然后这两个二维数组实施对应索引位置元素的求和操作，其结果为[[4, 4, 4], [6, 6, 6]]。没有被“约减”的维度（轴），其括号层次保持不变
 In [7]: a = np.array([[[1, 1, 1], [2, 2, 2]], [[3, 3, 3],[4, 4, 4]]])
 In [8]: a #输出验证
 Out[8]: 
 array([[[1, 1, 1],
  [2, 2, 2]],
  [[3, 3, 3],
  [4, 4, 4]]])
 In [9]: a.sum(axis = 0) #第0个轴方向约减求和
 Out[9]: 
 array([[4, 4, 4],
  [6, 6, 6]])
  • 上面运算过程更直观的演示如下图

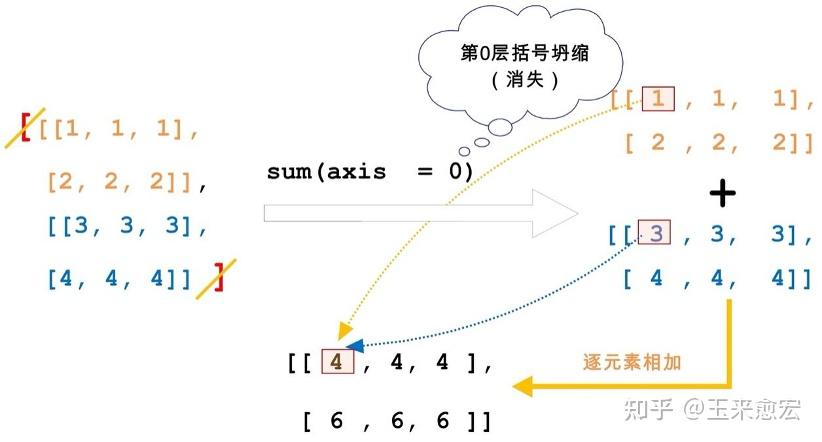
2. 当axis = 1时

  • axis=1，就是在第1个维度的元素之间进行求和操作，也就是拆掉中间层括号（即这个维度坍缩了），拆后对应的元素有[1, 1, 1], [2, 2, 2]和[3, 3, 3], [4, 4, 4]。

  • 需要注意的是，“约减”操作的实施范围为，将坍缩后同一个括号层次内的最大“颗粒度”的张量进行约减操作，即[1, 1, 1]和[2, 2, 2]向量相加，[3, 3, 3]和[4, 4, 4]向量相加。

  • 没有被“约减”的维度，其括号保持不变，结果得到[[3, 3, 3],[7, 7, 7]]

 In [10]: a.sum(axis = 1)
 Out[10]: 
 array([[3, 3, 3],
  [7, 7, 7]])
  • 上面运算过程更直观的演示如下图

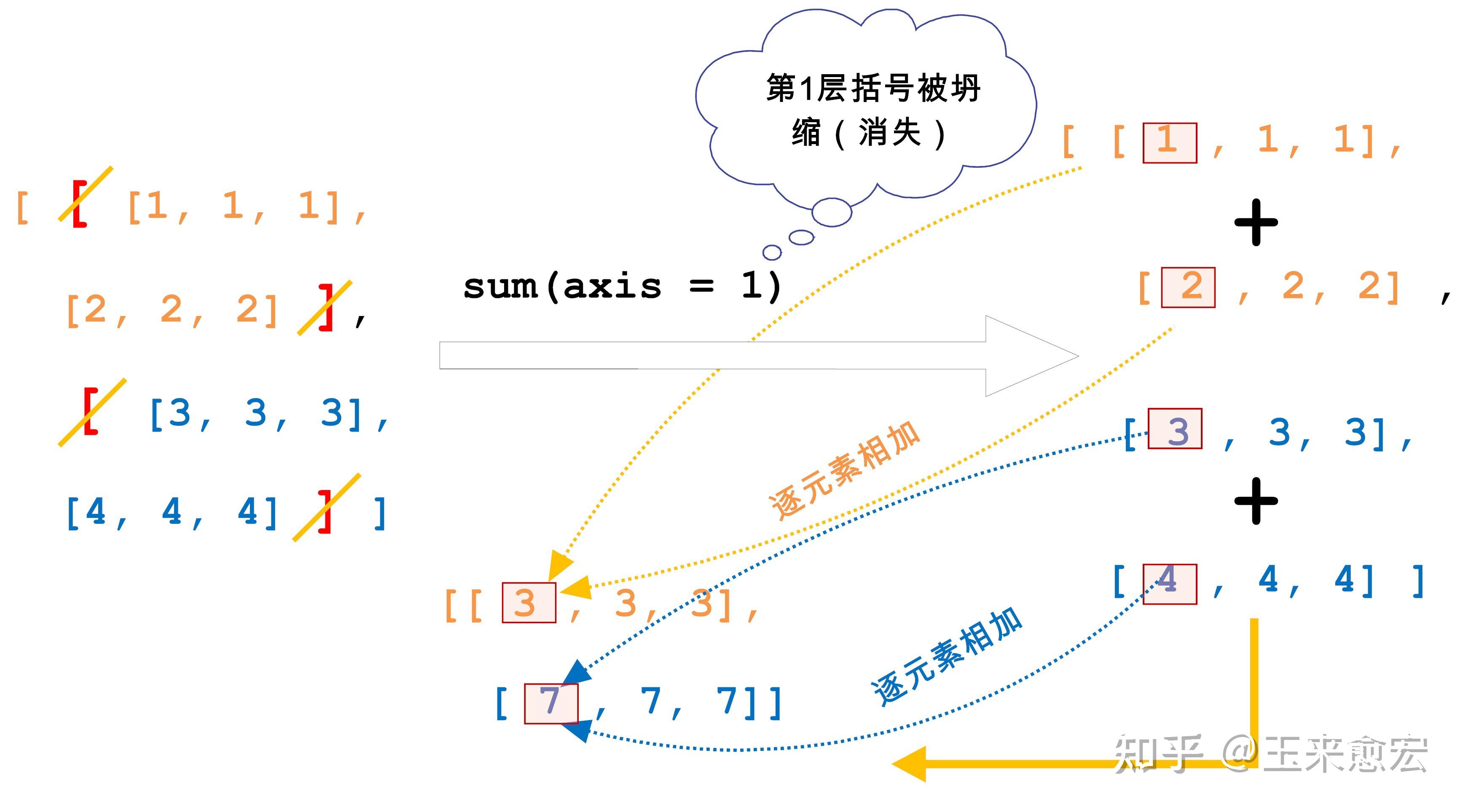
3. 当axis = 2时

  • axis = 2，就是拆掉最内层括号（rank = 2），然后对最内层括号元素实施求和操作，即1+1+1=3，2+2+2=6，3+3+3=9，4+4+4=12。

    实施“约减”操作之后，该层括号坍缩消失，其他维度的括号保留。结果得到[[3，6], [9，12]]

 In [11]: a.ndim  #查看张量a的维度
 Out[11]: 3
 In [12]: b = a.sum(axis = 2)   #在第2个轴上约减
 In [13]: b
 Out[13]: 
 array([[ 3, 6],
  [ 9, 12]])
 In [14]: b.ndim   #查看被约减后张量b的维度
 Out[14]: 2
  • 上面运算过程更直观的演示如下图

4. 小结

  • 事实上，每个维度经过“约减”之后都会消失。 这个有点类似于刘慈欣在《三体》小说中的“降维打击”。被“降维打击”的维度，由axis参数来指定，比如axis为0时，就是把0维“干掉”。具体如何干掉呢？其实就是在这个维度上执行“约减“操作！完整表述就是对0维执行sum操作，从而达到约减第0维的效果。其他维度的解释类似，不再赘述
  • 其他可实施约减的函数，如max（最大值）、min（最小值）和mean（均值）等，其轴方向的“约减”内涵与sum操作也是类似的，示例代码如下
 In [15]: a = np.linspace(1,9,9).reshape(3,3) 
 In [16]: a 
 Out[16]: 
 array([[1., 2., 3.],
  [4., 5., 6.],
  [7., 8., 9.]])
 In [17]: print(a.max(0),a.max(1),a.max()) #在第0轴、第1轴、不指定轴（全轴）进行最大值约减
 [7. 8. 9.] [3. 6. 9.] 9.0
 In [18]: print(a.mean(0),a.mean(1),a.mean()) #在第0轴、第1轴、不指定轴（全轴）进行均值约减
 [4. 5. 6.] [2. 5. 8.] 5.0
posted @ 2025-03-12 16:32  BigSun丶  阅读(71)  评论(0)    收藏  举报