Winograd Convolution 推导 - 从1D到2D
Winograd Convolution 推导 - 从1D到2D
1D Winograd 卷积
1D Winograd算法已经有很多文章讨论了,讨论得都比较清楚,这里就不再赘述,仅列出结论。
输入:四维信号
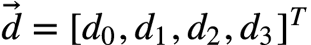
卷积核: 三维向量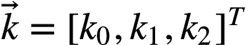
输出: 二维信号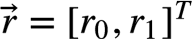
则可表示为:
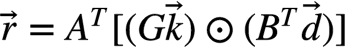
其中:
2D Winograd卷积
2D Winograd可以由1D Winograd外推得到,因此为解决2D Winograd问题,首先要重温1D 卷积解决的问题。在此复述一遍:
假设一个卷积核尺寸为3的一维卷积,假设每次我们输出2个卷积点,则我们形式化此问题:F(2, 3)。
因为输出为2,卷积核大小为3,对应的输入点数应该为4,则此问题表述为:
输入:四维信号
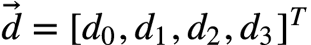
卷积核: 三维向量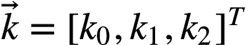
因此,此卷积的矩阵乘形式应为:
请记住这个形式是Winograd算法解决的问题,后续2D算法将化归为这个问题。
下面我们来定义2D 卷积问题,将1D卷积扩展一维:
假设一个卷积核尺寸为3x3的二维卷积,假设每次我们输出2x2个卷积点,则我们形式化此问题:F(2x2, 3x3)。
因为输出为2x2,卷积核大小为3x3,对应的输入点数应该为4x4,则此问题表述为:
输入:
卷积核:因此,此卷积的矩阵乘形式应为:
从这个式子里,我们可以看到1D卷积的影子,这个影子在我们对矩阵作了分块后会更加明显。
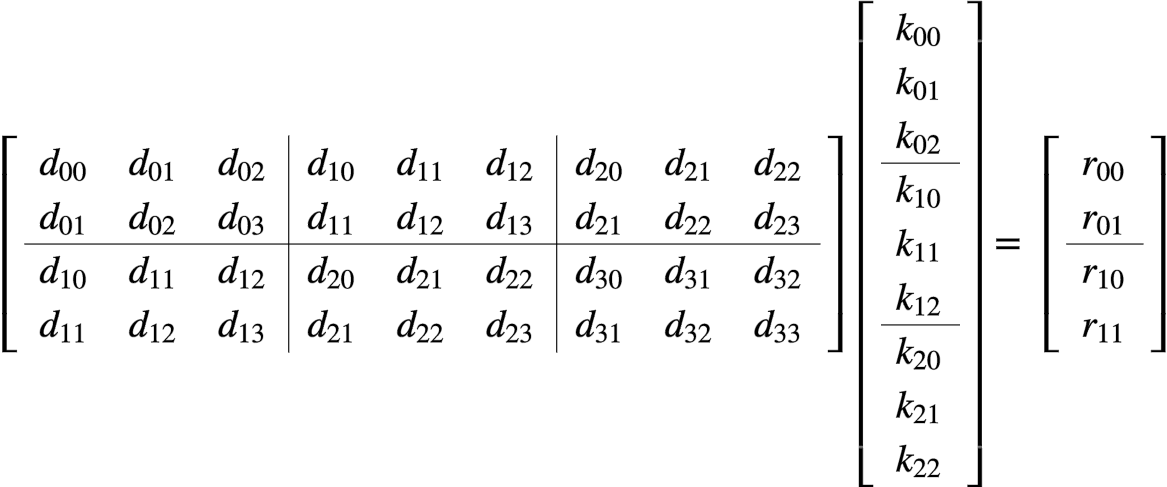
再明显一点,我们写成分块矩阵乘的形式:
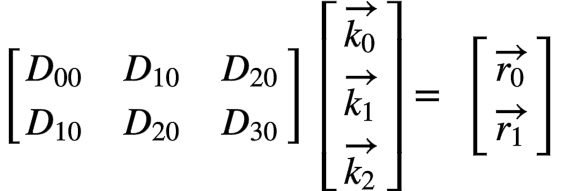
至此,我们对2D卷积推导出了跟1D形式一致的公式,只不过1D中的标量在2D中变成了小矩阵或者向量。
实操粉
对实操粉而言,到这个形式为止,已经可以写代码了。
由1D Winograd可知,我们可以将该式改写为Winograd形式, 如下:
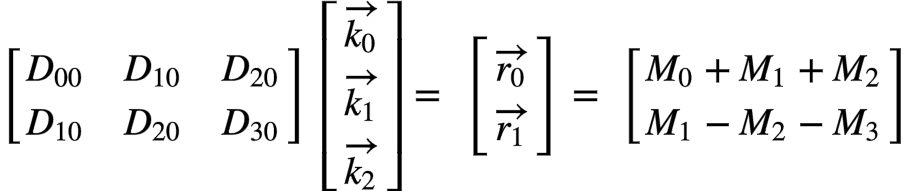
其中:

注意,这四个M的计算又可以用一维的F(2, 3) Winograd来做,因此2D Winograd是个嵌套(nested)的算法。
理论粉
对一个有追求的理论粉来说,只是得到可以写程序的递归表达肯定是不完美的,他们还是希望有一个最终的解析表达的。其实也很简单,我们把上面的式子规整规整,使得输出成为一个标准的2x2矩阵,有:
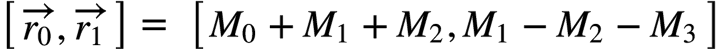
可以写为:
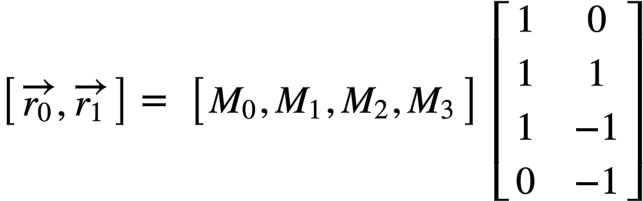
依1D Winograd公式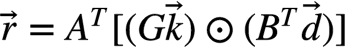 , 并结合各M的公式,有下式。
, 并结合各M的公式,有下式。
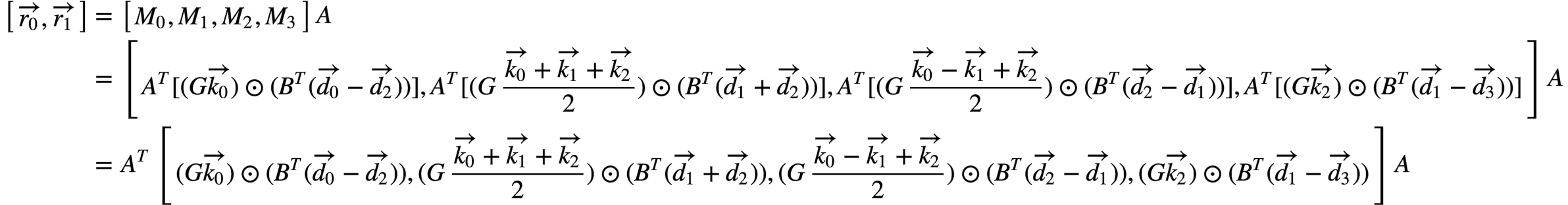
注意到像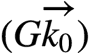 这些都是2维列向量,hadamard product和concat可以交换而不影响结果,因此:
这些都是2维列向量,hadamard product和concat可以交换而不影响结果,因此:
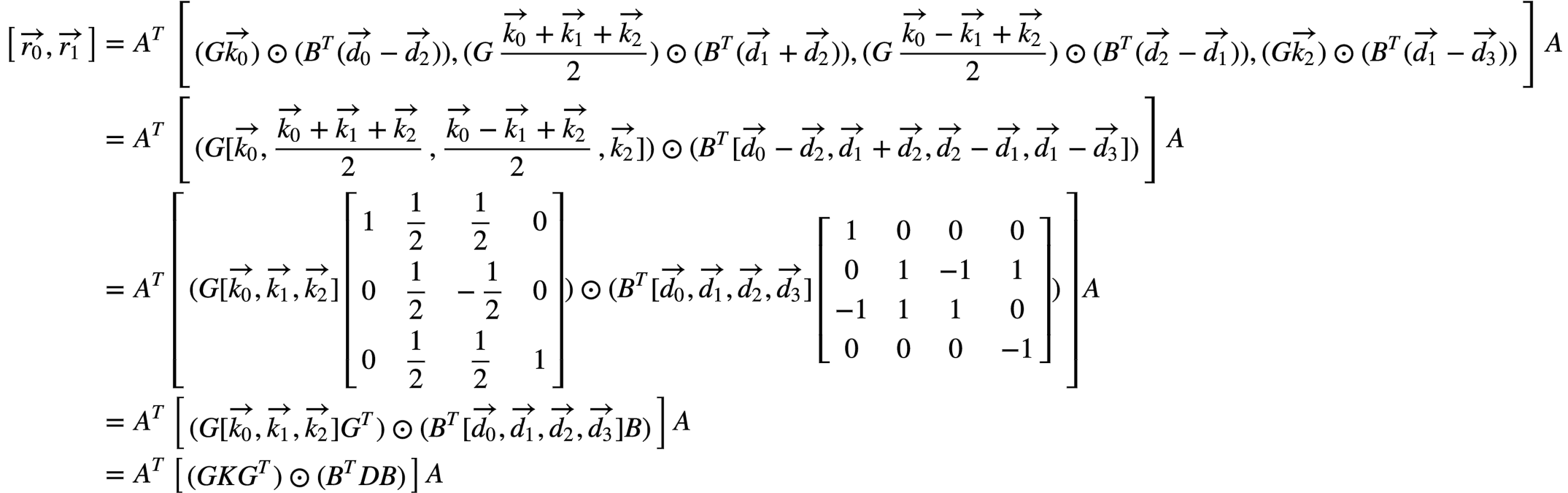
至此证得。



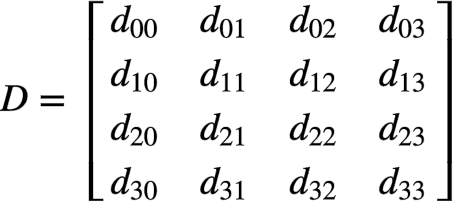
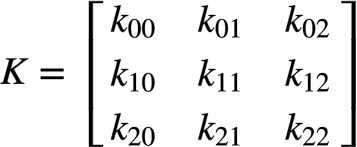
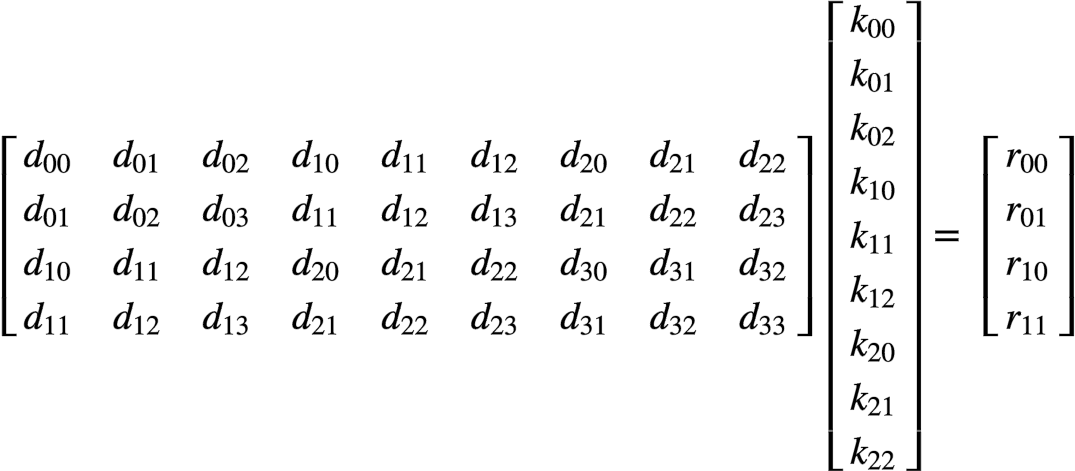


 浙公网安备 33010602011771号
浙公网安备 33010602011771号