神秘题记录
图论
CF1368G Shifting Dominoes
有一个 \(n\times m\) 的棋盘,被 \(1\times2\) 的骨牌覆盖,保证 \(2\mid nm\)。
现在你需要执行以下操作:
- 移去恰好一张骨牌。
- 将一张骨牌沿着其长边进行移动。你可以进行这一步任意次。
- 你需要保证在任意时刻,每张骨牌的位置与其初始位置至少有一个公共格子。
求你可以得到的所有可能的最终局面的数量。
\(nm\le2\times10^5\)。
对于某一个格子,假如它最终是空的,要么一开始覆盖它的骨牌被移去,要么覆盖它的骨牌照它的反方向移动一格。
覆盖它的骨牌照它的反方向移动一格,相当于把空位从反方向两格的位置移动到这个位置。
按照这个方式建图,建出来会是一棵棵基环树,手玩发现不会有环(证明不会)。
于是最后会是一个森林,给网格黑白染色,黑白格之间不会连边。
所以移走某个骨牌 \(A\) 后,空位能到达的状态必然是 \(A\) 的两个格子的子树,黑白格不连边,于是这两棵子树不会有交。
拍扁 dfn 序,转化为矩形面积并,扫描线+线段树。
时间复杂度 \(O(S\log S)\)(\(S=nm\))。
CF1458D Flip and Reverse
给一个 01 串 \(s\)。
每次可以选择一个 01 个数相等的区间 \([l,r]\),翻转(reverse)\(s[l\dots r]\),并反转(flip)\(s[l\dots r]\)。
求最后能得到的字典序最小的 \(s\)。
多组数据,\(\sum|s|\le 5\times10^5\)。
记一个值 \(x\),初值为 \(0\)。
扫一遍 \(s\),遇到 \(1\) 则 \(x\gets x+1\),否则 \(x\gets x-1\)。
给变化前后的 \(x\) 连边(遇到 \(1\) 则 \(x\to x+1\),否则 \(x\to x-1\)。)
初始 \(s\) 为图的一条欧拉路径。
发现一次操作是把一个环所有边反向。
经典结论,欧拉路径随便选,不需要考虑初始方向。
把图变为无向图,最终的 \(s\) 为一条欧拉路径。
字典序最小,可以贪心,在 \(x\) 处贪心先走 \(x-1\)。
但发现 \(x-1\Leftrightarrow x\leftrightarrow x+1\) 会寄。
增加条件:若 \(x\to x+1\) 的边只有一条,那么 \(x\to x+1\) 的边要有两条才能先走 \(x\to x+1\)。
单次询问时间复杂度 \(O(|s|)\)。
CF1466H Finding satisfactory solutions
有 \(n\) 人和 \(n\) 个物品。
每个人有一个排列 \(s_i\) 表示他想要物品的优先程度的排名。
给人分配物品,使得最优的分配方案 \(p\) 不会被偏序。
可以 \(s\) 对应的证明 \(p\) 唯一。
被偏序指:存在更优的分配方案 \(p'\) 使得每个人分到的物品不劣,并且有人分到更优的物品。
\(n\le 40\),时限 \(5s\)。
每个 \(s\) 对应唯一的最优 \(p\) 唯一,考虑如何找到 \(p\)。
先假设每个人取得最有物品,建图 \(i\to s_{i,1}\)。
建出来会是内向基环树森林,找到环,环上的点一定是最优的。于是不能动环,删掉环上的点和边。
删完后若有点 \(x\) 原本连上环上的点 \(s_{x,1}\),但 \(s_{x,1}\) 被删除了,退而求其次 \(x\to s_{x,2}\)。
以此类推最后会得到唯一的 \(p\)。
题目给定 \(p\),能得到最终的环,即 \(i\to p_i\) 的环。
分类每一层删除的环。
考虑第 \(k\) 层环上一个点,假设第 \(k-1\) 层有 \(X=cnt_{k-1}\) 个点,\(k\) 层及以后有 \(Y=suf_{k-1}\) 个点。它的 \(s\) 的方案是:
第 \(k\) 层有 \(siz\) 个点的方案:
第 \(k\) 层有 \(len\) 个点的环的贡献:
于是可以开始 DP,\(dp_{s,i,j,k}\) 表示状态为 \(s\),当前环长 \(i\),当前层点数 \(j\),上一层点数 \(k\) 的方案数。
状态数 \(s\) 的数量很少,好像大概只有 \(1500\) 个左右。
复杂度就是 \(1500\) 乘上若干个 \(n\)。根本跑不满所以能过。
CF1477D Nezzar and Hidden Permutations
给定一张 \(n\) 个点 \(m\) 条边的简单无向图,构造两个排列 \(p,q\),使得:
- 对任意 \((u,v)\in E\),\((p_u-p_v)(q_u-q_v)>0\).
- 在此基础上,最大化 \(|\{i\mid p_i\neq q_i\}|\).
多组数据,\(1\le \sum n,\sum m\le 5\times 10^5\),时限 \(5s\)。
题意转化:将无向图定向为 DAG,构造两个拓扑序 \(p,q\) 使得 \(|\{i\mid p_i\neq q_i\}|\) 最大。
对于一个 DAG,一个点 \(x\) 在拓扑序中的位置固定当且仅当所有点都能到达 \(x\) 或者被 \(x\) 到达。
此时若有 \(s\) 个点能够到达 \(x\),那么必有 \(p_s=q_s=x\)。
称这样的点为“固定点”。
所以固定 DAG 答案上界是 \(n\) 减去“固定点”的个数。
在无向图内,若一个点度数为 \(n-1\),那么定向后它一定是“固定点”。
把度数为 \(n-1\) 的点 ban 掉之后,新图剩下 \(n'\) 个点,此时度数为 \(n'-1\) 的点又一定是“固定点”。
依次类推,最后剩下的点是答案的上界。
称剩下的图为 \(G\),\(G\) 中不存在点度数为 \(|G|-1\)。
反图 \(\neg G\) 的每个连通块都至少有两个点。
发现 \(\neg G\) 的一个菊花一定可以构造,设菊花根为 \(rt\),叶子为 \(a_1,a_2,\dots,a_k\)。构造:
- \(p=\{rt,a_1,a_2,\dots,a_k\}\)
- \(q=\{a_1,a_2,\dots,a_k,rt\}\)
trick:菊花剖分。
当前点 \(x\) 未被剖分。
- 若所有 \(x\to y\) 的 \(y\) 均未被剖分,剖出以 \(x\) 为根的菊花。
- 若存在 \(x\to y\) 的 \(y\) 已被 \(rt\) 为根的菊花剖分:
- 如果 \(rt\) 为根的菊花还有大于两个点,直接“抢夺” \(y\) 到 \(x\) 为根的菊花。
- 如果 \(rt\) 为根的菊花只有两个点,“移形换影” \(y\) 为菊花的根,\(x,rt\) 为叶子。
反图用 set 维护,时间复杂度 \(O(n\log n)\)。
\(\small\mathbf{注意输出节点在拓扑序中的位置而不是拓扑序!}\)
CF986F Oppa Funcan Style Remastered
给定 \(n,k\),求是否存在排列 \(p\) 使得 \(i\to p_i\) 所有环的环长都是 \(k\) 的因数,不能自环。
多组数据,\(T\le 10^4\),\(n\le 10^{18}\),\(k\le 10^{15}\),最多 \(T_k=50\) 个不同的 \(k\)。
转化题意,求 \(n\) 是否能被划分为若干个 \(k\) 的非 \(1\) 因数之和。
显然可以只考虑 \(k\) 的质因数。
分类讨论 \(k\) 的质因数个数 \(d\):
- \(d=1\),\(k\) 形如 \(p^a\),判断 \(p|n\)。
- \(d=2\),\(k\) 形如 \(p^a q^b\),判断 \(q\times(\dfrac{n}{q}\bmod p)\le n\)
- \(d\ge 3\),最小质因子至多 \(\sqrt[3]{10^{15}}=10^5\),直接同余最短路。
分解使用 Pollard Rho。
时间复杂度 \(O(T_k k^{\frac{1}{4}}+T_k k^{\frac{1}{3}}+T_k\log k+T)\)。
CF1148G Gold Experience
有 \(n\) 个点,带点权 \(a\),两点 \(i,j\) 若满足 \(\gcd(a_i,a_j)>1\) 则连一条无向边 \((i,j)\)。
定义一张图中的某一个点是“好的”,当且仅当它和其它所有点有连边。
构造一个大小恰好为 \(k\) 的导出子图,使得每个点都是“好的”或者每个点都不是“好的”:
\(6\le 2\cdot k\le n\le 2\times 10^5\),\(2\le a_i\le 10^7\)。
时限 \(2s\),空限 \(1000M\)。
\(\gcd>1\) 的限制太奇怪了,取补图,转化为 \(\gcd=1\),限制为所有点都是孤立点或者没有孤立点。
假如所有点度数 \(<2\),那么最大独立集至少有 \(\dfrac{n}{2}\) 个点,选择某个大小为 \(k\) 的独立子集即可。
点 \(x\) 度数 \(\ge 2\),则可以提取出三元链 \(y\to x\to z\)。三元链可以凑出大小为 \(2\) 或 \(3\) 的子图。
令 \(f(x)\) 为前 \(x\) 个数的图中非孤立点个数。
二分 \(f(p-1)+3<k\le f(p)+3\) 的最小 \(p\)。
有 \(m=f(p)-f(p-1)-1\) 个点只与 \(p\) 连边,可以取出 \(2\sim m\) 个。
又有三元链可以多调整 \(1\) 个位置,就做完了。
将每个数多余质因子去除,暴力枚举因数莫反。
记 \(d\) 为最大值的满足前 \(d\) 个质数的积大于 \(V\)。(实际 \(d\le 8\))
时间复杂度 \(O(n2^d\log n+nd2^d+V)\),空间复杂度 \(O(n2^d)\)。
其实跑得挺快。
CF1240F Football
给一个 \(n\) 点 \(m\) 边的无向图,有 \(k\) 种颜色。
构造一种对边染色的方案使得:
对于每个点,记 \(s_i\) 为连向它的颜色为 \(i\) 的边数,需要满足 \(s\) 极差不超过 \(2\)。
\(3\le n\le 100\),\(0\le m\le 1000\),\(1\le k\le 1000\)。
拆点,原图边 \((x,y)\) 变为新图边 \((x,y+n)\),也就是变成二分图。
给二分图边染色,让每个点极差不超过 \(1\),合并回原图极差就不超过 \(2\)。
trick:二分图对边 \(k\) 染色,每个点度数 \(\le k\),则可以做到出边颜色两两不同。
假设当前边 \((u,v)\),\(u\) 出边未染颜色 \(a\),\(v\) 出边未染颜色 \(b\)。
若 \(a=b\),直接将 \((u,v)\) 染为 \(a\)。
反之 \(a\ne b\),称这个冲突为 \(f(u,v,a,b)\)。
找到 \(v\overset{a}{\rightarrow}u'\),将 \((u,v)\) 染为 \(a\),将 \((u',v)\) 染为 \(b\)
- \(u'\) 之前未染色 \(b\),解决。
- \(u'\) 之前未染色 \(b\),找到冲突 \(u'\overset{b}{\rightarrow}v'\),求解子问题 \(f(u',v',b,a)\)。
这样若递归会 \(u\),二分图必定只有偶环,则会是 \(f(u,?,a,b)\) 的形式。
但 \(u\) 之前还没有出边被染为 \(a\) 颜色,不存在 \(?\) 点,矛盾,故一定会递归到有解。
若一个点出边有 \(kx+y\) 条,拆成 \(x\) 个度数为 \(k\) 的点和一个的数为 \(y\) 的点。
让每个点连出的边颜色两两不同,再合并,就行了。
时间复杂度 \(O(m^2)\)。
CF1268D Invertation in Tournament
给一个 \(n\) 点的竞赛图,称翻转 \(x\) 为反转 \(x\) 的出入边的方向。
构造最少翻转次数,使得图强连通。并求最少翻转次数的方案数。
\(3\le n\le 2000\),时限 \(3s\)。
有很多非常牛的结论。
结论 \(1\):竞赛图缩点之后一定是一条 \(k\) 个点的链,并且对于所有 \(i<j\) 都有边 \((i,j)。\)
结论显然。
结论 \(2\):\(n>3\) 个点的强连通竞赛图可以删除其中一个点,使得剩下的图强连通。
假设有一个 \(n-1\) 个点的竞赛图 \(G\),加入点 \(n\) 和它连的 \(n-1\) 条边,得到强连通竞赛图 \(G'\)。
称 \(G\) 缩点之后的连通分量链为 \(S_1,S_2,\dots,S_k\)。
\(k=1\)。
\(G\) 强连通,\(G'\) 删除 \(n\) 后强连通。
\(k\ge 3\)
由于 \(G\) 强连通,在 \(G\) 中 \(S_k\) 一定能走到 \(S_1\),那么只能是 \(S_k\to n\to S_1\)。
令 \(x\in S_1,y\in S_n\),有 \(y\to n\to x\)。
根据结论 \(1\),所有点在 \(G\) 中都可到达 \(x\),也都可被 \(y\) 到达。
\(G'\) 中删去任意点 \(p\in S_m\),\(1<m<k\),不影响所有点都可到达 \(x\) 和可被 \(y\) 到达。
又 \(x\to n\to y\),任意点 \(\to x\to n\to y \to\) 任意点,所以 \(G'\) 去除点 \(p\) 强连通。
\(k=2\)
由于 \(n>3\),必有 \(|S_1|\ge 2\) 或 \(|S_2|\ge 2\),从这个集合中删除一个点 \(p\)。
同理,只要 \(p\) 不是 \(x\) 或 \(y\),则仍不影响上述性质,\(G'\) 去除点 \(p\) 仍强连通。
得证。
推论:\(n>3\) 个点的强连通竞赛图可以翻转其中一个点,使得它仍强连通。
翻转你结论 \(2\) 中要删除的那个点即可。
结论 \(3\):\(n>6\) 个点的强连通竞赛图,可以翻转至多 \(1\) 个点使得原图强连通。
称竞赛图 \(G\) 缩点之后的连通分量链为 \(S_1,S_2,\dots,S_k\)。
\(k=1\)
不需要翻转,直接强连通。
\(k\ge 3\)
选择任意点 \(p\in S_m\),\(1<m<k\),翻转 \(p\)。
有路径:任意点 \(\to S_k\to p\to S_1 \to\) 任意点,图 \(G\) 强连通。
\(k=2\)
必有 \(|S_1|>3\) 或 \(|S_2|>3\)。
\(|S_1|>3\)
根据结论 \(2\) 推论,存在 \(x\in S_1\) 使得翻转 \(x\) 后 \(S_1\) 强连通,翻转 \(x\)。
找到 \(y\in S_1,y\ne x\),有环 \(S_2\to x\to y\to S_2\)。
又 \(S_1,S_2\) 强连通,则翻转 \(x\) 后 \(G\) 强连通。
\(|S_2|>1\)
相同的,存在 \(x\in S_2\),使得翻转 \(x\) 后 \(S_2\) 强连通,翻转 \(x\)。
同理翻转 \(x\) 后 \(G\) 强连通。
得证。
兰道定理推论:竞赛图强连通的充要条件是,按照出度 \(d\) 排序顶点,\(\nexists k\in[1,n),\sum\limits_{i=1}^k d_i={k\choose 2}。\)
充分性:设前 \(k\) 个点度数之和为 \(k\choose 2\),有它们的导出子图有 \(k\choose 2\) 条边,即它们不向其他点连边。
必要性:
假设图 \(G\) 是非强连通竞赛图,缩点之后的连通分量链为 \(S_1,S_2,\dots,S_k\)。
根据结论 \(1\),所有 \(x\in S_i(i<k)\) 都有 \(x\to y(y\in S_k)\),则 \(d_x\ge |S_k|\)。
又有 \(\forall x\in S_k,d_x\le |S_k|\),则 \(d\) 的前 \(k\) 小为 \(S_k\) 所有点。
又因为 \(S_k\) 内部是竞赛图,所以 \(\sum\limits_{i=1}^{|S_k|}d_i={|S_k|\choose 2}\)。
这样就可以 \(O(n)\) 判断竞赛图是否强连通了。
\(n\le 6\) 直接 \(2^n\) 枚举翻转点集,\(n>6\) 我们枚举翻转那个点,排序使用桶排。
时间复杂度 \(O(n^2)\)。
CF487E Tourists
给一张 \(n\) 点 \(m\) 边的带点权连通无向图,无重边自环,\(q\) 次操作:
- 单点修改点权。
- 查询 \(u\to v\) 所有不重点路径中的最小点权。
\(1\le n,m,q\le 10^5\)。
这就是广义圆方树?
路径不重点,缩点双,每个点双建方点连向内部所有点(圆点),这样就能建出广义圆方树。
网上的图:

查询就是路径方点邻域和圆点的最小值。
trick:邻域信息只维护儿子。
每个方点开 multiset 维护儿子信息,特判查询路径 lca 为方点。
然后树剖上线段树。时间复杂度 \(O(n\log n+m+q\log^2 n)\)。
[AGC045E] Fragile Balls
有 \(n\) 个球,\(m\) 个盒子。
初始 \(i\) 号球在 \(A_i\) 号盒子中,需要把它移动到 \(B_i\) 号盒子,它只能移动 \(C_i\) 次。
每一次移动形如:选择至少有两个球的盒子 \(x\),选择 \(x\) 中的球 \(i\),将其移动到另一个盒子 \(y\)。
求是否有解,以及有解的最少移动次数。
保证最终状态⾥每个盒⼦都有球。
\(1\le n,m\le 10^5\),\(1\le A_i,B_i\le n\),\(1\le C_i\le 10^5\)。
感谢 pb 的意识流题解。
建图,\(A_i\to B_i\)。(图上的点是盒子!!!边是球!)
先考虑 \(C_i=1\) 的情况,即每条边只能动一次。
显然若点 \(x\) 入度 \(in_x=0\) 并且出度 \(out_x>1\) 则肯定无解,特判这种情况。
如果某一个球 \(i\) 已经到 \(B_i\) 了,它所在的盒子 \(B_i\) 若有其他球 \(j\),则此时 \(B_i\) 满足有两个球的限制。
可以直接将 \(j\) 挪到 \(B_j\),这样 \(j\) 就到 \(B_j\) 了。
接下来称图上某个点 \(x\) “归位”指盒子 \(x\) 内存在球 \(i\) 使得 \(B_i=x\)。
根据上面这种做法,假如 \(x\) 归位了,那么图上所有 \(x\to y\) 的 \(y\) 也能归位。
这启发我们考虑强连通分量,假如强连通分量内部有一个点归位了,那么整个强连通分量都能归位。
考虑某一个缩点后在 DAG 上入度为 \(0\) 的强连通分量 \(S\)。
假设我们让 \(S\) 所有点归位了,那么 DAG 上 \(S\) 的儿子会获得一些已归位的点(\(S\) 向其儿子连的边),然后 \(S\) 的儿子所有点都可以归位,以此类推 \(S\) 所有后继都可以全部点归位。
对于某个弱连通块,只要其入度为 \(0\) 的强连通分量全部归位,那么这个弱连通块就解决了。
于是考虑如何让 \(S\) 归位某个点。
假设 \(S\) 内部存在简单环 \(x\to y\to z\to \dots\to x\),并且 \(x\) 的出度 \(out_x>1\)。
由于 \(out_x>1\),此时盒子 \(x\) 有大于一个球,把代表 \(x\to y\) 的球移动至 \(y\)。
这是盒子 \(y\) 又有大于一个球,将代表 \(y\to z\) 的球移动至 \(z\)。
以此类推,可以将最终整个简单环上的点都归位。
强连通分量简单环随便找,难点在于 \(out_x>1\)。
若一个 \(S\) 内部无 \(out_x>1\),则 \(S\) 根本无法操作,必定无解。
- 若 \(S\) 所处弱连通块仅 \(S\) 一个强连通分量,有无解取决于是否存在 \(x\in S,out_x>1\)。
- 只有简单环才能使得 \(\nexists x\in S,out_x>1\)。
- 若 \(S\) 不止 \(S\) 一个强连通分量,即 \(S\) 在 DAG 上有出度。
- 若 \(|S|=1,S=\{x\}\),则 \(in_x=0,out_x>0\),已被特判。
- 若 \(|S|>1\),则 \(\forall x\in S,out_x\ge 1\),又 \(S\) 在 DAG 上有出度,则存在 \(x\in S,out_x>1\)。
结论:有解当且仅当每个点数 \(>1\) 的弱连通块存在点 \(x\) 使得 \(out_x>1\)。
充分性上面证了,必要性显然:若 \(\forall x,out_x\le 1\),那么所有点动都动不了。
结论也相当于:有解当且仅当每个非自环的弱连通块不是简单环。
\(\rule{20cm}{0.05em}\\\)
接下来考虑 \(C_i>1\) 的情况,并考虑最小化操作次数。
对于一条边(一个球),它可以移动到别处“帮助”别的弱连通块,将其抽象成带价值和代价的物品。
设 \(k\) 为非自环简单环连通块数量,需要选择物品使价值 \(\ge k\)。(特判 \(k=0\))
答案初始设为 \(k+\sum\limits_{i=1}^m[A_i\ne B_i]\),计算额外的代价。
分类讨论球 \(x\)(边 \(A_x\to B_x\))和其连通块 \(S\) 情况:
- \(a\):\(A_x\ne B_x\),非自环。
- \(S\) 是简单环,要“帮助”一次才能移动这个连通块,这个代价已经在最后得到的 \(k\) 价值中计算,故代价为 \(0\),球 \(x\) 都可以挪出去 \(C_x-1\) 次再挪回来,价值为 \(C_x-1\)。
- \(S\) 非简单环,\(S\) 可以直接内部归位,价值为 \(0\),同理价值为 \(C_x-1\)。
- \(b\):\(A_x=B_x\),自环。
- \(S\) 仅 \(x\) 自环,要“帮助”一次才能移动,最后还得用一次挪回来,代价为 \(2\),价值为 \(C_x-2\)。
- \(S\) 非简单环,同样每个球还得用一次挪回来,代价为 \(1\),价值为 \(C_x-1\)。
特别地,如果没有 \(a.2\),我们一开始只能使用 \(b.2\)。
显然每类物品都是先取价值大的,将每一类物品从大到小排序。
\(a\) 类物品免费直接取,取完 \(\ge k\) 就直接搞定。
否则设 \(b.1\) 取 \(X\) 个,\(b.2\) 取 \(Y\) 个,\(b.1\) 前 \(X\) 大价值和 \(+\) \(b.2\) 前 \(Y\) 大价值和 \(\ge k\),代价 \(2X+Y\)。
对每个 \(X\) 二分出最小的 \(Y\),复杂度 \(O(n\log n)\),双指针可以 \(O(n)\)。
你甚至可以 \(O(n^2)\) 枚举 \(X,Y\),强烈吐槽 AT 数据水。
使用了并查集处理弱连通块,所以是 \(O(n\alpha(n))\)。
CF750H New Year and Snowy Grid
有一个 \(n\times m\) 的棋盘,初始有一些格子是障碍。
\(q\) 次询问,加入 \(k\) 个新的障碍后是否存在 \((1,1)\to (n,m)\) 的两条不相交路径。
询问之间相互独立。
\(2\le n,m\le 10^3\),\(1\le q\le 10^4\),\(1\le k\le 10\)。
先考虑如何判定存在 \((1,1)\to (n,m)\)(左上到右下)的两条不相交路径。
这相当于最小割 \(\ge 2\)。
在右上和左下边界处加一圈蓝点。

\((1,1)\to (n,m)\) 不能连通相当于左下和右上的蓝点通过黑点八连通。
接下来“连通”指八连通,“几乎连通”指两个点之间再加一个点就连通。
则最小割 \(\le 1\) 相当于:存在加上一个额外的黑点的方案,使左下和右上的蓝点通过黑点连通。
先把原图的连通块处理出来,新加入 \(k\) 个点只会多 \(O(k)\) 个连通块与左下或右上连通。
处理出这 \(O(k)\) 个连通块,称 \(S\) 是与左下连通的集合,\(T\) 是与右上连通的集合。
无解情况:
-
新增的 \(k\) 个黑点后,左下和右上连通。
判一下就行。
-
新增的点 \(x\in S\),与点 \(y\in T\) 几乎连通。
对 \(k\) 个新增的点枚举与其几乎连通的点即可。
-
连通块 \(x\in S,y\in T\),\(x\) 与 \(y\) 几乎连通。
直接暴力枚举 \(S\) 和 \(T\) 中的连通块判是否几乎连通。
时间复杂度 \(O(nm+qk^2)\)。
CF798E Mike and code of a permutation
对于一个 \(1\sim n\) 的排列 \(p\),定义它的编码 \(a\) 为:
\(i=1\dots n\),\(a_i\) 为第一个未标记的 \(j\) 满足 \(p_j>p_i\),标记 \(j\),没有合法的 \(j\) 则 \(a_i=-1\)。
现在给出 \(a\),构造 \(p\)。
\(1\le n\le 5\times 10^5\)。
接下来 \(a_i=-1\) 认为是 \(a_i=n+1\)。
令 \(b_i\) 为 \(i\) 在 \(a\) 中的位置,若 \(a\) 中没有 \(i\) 则 \(b_i=n+1\)。
在 \(a_i=j\) 时,能得到信息:
-
\(p_j>p_i\),即题目给的条件,转换 \(p_{a_i}>p_i\) 得 \(p_i>p_{b_i}\)。
-
\(k\in[1,j-1]\),\(k\) 之前未标记,则 \(p_k<p_i\)。
若 \(k\) 之前未标记,意味着存在 \(b_k>i\),即 \(k\) 在 \(i\) 后标记。
对于所有 \(p_x<p_y\) 的限制连边 \(x\to y\),拓扑序就是 \(p\)。
trick:求拓扑序的反图 dfs 方法。
当前 \(\operatorname{dfs}(x)\):
找到反图上 \(x\to y\) 的 \(y\),若 \(y\) 没被 dfs 过,则 \(\operatorname{dfs}(y)\)。
拓扑 \(x\)。
dfs(x){ vis[x]=true; for(x 的儿子 y)if(!vis[y])dfs(y); topo.push_back(x); }
这样只需要知道 \(x\) 在反图上还未 dfs 的儿子 \(y\) 就能拓扑了。
反图上 \(x\to y\) 即限制 \(p_x>p_y\),可得 \(y=b_x\) 或 \(y<a_x,b_y>x\)。
线段树维护 \(b\) 区间 max,dfs 到 \(x\) 时删掉 \(b_x\)。
时间复杂度 \(O(n\log n)\)。
CF718E Matvey's Birthday
有一个长为 \(n\) 的字符串 \(s\),生成一个无向图:
- \(1\le i<n\) 的 \((i,i+1)\) 连边。
- \(s_i=s_j\) 的 \((i,j)\) 连边。
求图的直径 \(D\) 和有多少点对 \((x,y)\) 的最短路为 \(D\)。
\(1\le n\le 10^5\),字符集 \(a\sim h\)。
记 \(k=8\) 为字符集大小。
不难发现任意两点最短路不可能包含三个相同字符的点,即最短路 \(\le 2k-1=15\)。
记 \(f_{x,c}\) 为位置 \(x\) 到字符 \(c\) 的距离,\(g_{c1,c2}\) 为任两个字符 \(c1,c2\) 的距离的最小值。
\(f\) 和 \(g\) 可以多源 bfs \(O(nk)\) 求出:
bfs 颜色 \(c\),队列加入所有 \(s_i=c\) 的点 \(i\),距离为 \(0\)。
当前队顶 \(x\),距离为 \(f_{x,c}=d\)。
若之前没有过颜色为 \(s_x\) 的点,\(g_{c,s_x}=d\)。
将所有 \(s_i=s_x\) 且 \(i\) 不在队列中的 \(i\) 加入队列,距离 \(d+1\)。
若 \(x-1,x+1\) 没有进过队列,加入它,距离 \(d+1\)。
现在考虑如何计算 \(dis(i,j)\)(\(j<i\))。
-
\(i-j\le 15\)
\[dis(i,j)=\min(\min_c f_{i,c}+f_{j,c}+1,i-j) \]直接 \(O(nk^2)\) 暴力计算。
-
\(i-j>15\)
\[dis(i,j)=\min_c f_{i,c}+f_{j,c}+1 \]有一个性质:bfs 的过程说明 \(f_{i,c}=g_{s_i,c}\ \operatorname{or}\ f_{i,c}=g_{s_i,c}+1\)。
考虑状压,\(S_i\) 为 \(k\) 位二进制数,第 \(c\) 位为 \(0/1\) 表示 \(f_{i,c}=g_{s_i,c}/f_{i,c}=g_{s_i,c}+1\)。
开桶 \(C_{c,t}\) 表示 \(j<i-15,s_j=c,S_j=t\) 的 \(j\) 的个数。
直接枚举 \(c,t\) 计算贡献,时间复杂度 \(O(nk^2 2^k)\),预处理一下就是 \(O(k^3 4^k+nk2^k)\)。
总时间复杂度 \(O(nk+k^3 4^k+nk2^k)\)。
P5292 [HNOI2019] 校园旅行
有一个 \(n\) 点 \(m\) 边的无向图,每个点有 \(0/1\) 点权。
一条路径是好的当且仅当经过的点点权组成回文串。
\(q\) 次询问 \(u,v\) 之间是否存在好的路径。
注意路径可以重复经过点、边。
\(1\le n\le 5\times 10^3\),\(1\le m\le 5\times 10^5\),\(1\le q \le 10^5\)。
有明显的 \(O(m^2)\) 做法:
bfs 到合法点对 \((u,v)\),扩展 \(u'\to u,v\to v'\),使得 \(u',v'\) 点权相同,加入点对 \((u',v')\)。
考虑删除无用的边使得边数更少。
称边 \((u,v)\) 为“同色边”指 \(u,v\) 点权相同,其它边称为“异色边”。
提出同色边组成的图 \(G_0\)。
点 \(u,v\) 在 \(G\) 中所属连通块中 \(S_u,S_v\),若 \(u,v\) 之间存在好的路径,那么扩展一下:
\(u,v\) 在 \(S_u,S_v\) 中各走 \(x\) 步到达 \(u',v'\),\(u',v'\) 之间也存在好的路径。
对于 \(G_0\) 的连通块 \(S\):
-
若 \(S\) 中存在奇环,\(S\) 中任意两点 \(u,v\) 均存在 \(u\to v\) 的长度为奇数或偶数的路径。
只保留 \(S\) 的一棵带奇环的生成基环树(或者保留一棵生成树加上自环)。
-
若 \(S\) 为二分图,\(S\) 中任意两点 \(u,v\) 的路径奇偶固定了。
只保留 \(S\) 的一棵生成树。
异色边组成的图 \(G_1\) 同样操作,这样边数变为 \(O(n)\)。
直接跑上面的 bfs 做法,时间复杂度 \(O(n^2+m+q)\)。
[AGC016D] XOR Replace
有两个长为 \(n\) 的序列 \(a,b\)。
一次操作可以选择 \(x\), \(a_x\gets \bigoplus\limits_{i=1}^n a_i\)。
求最少几步把 \(a\) 变为 \(b\),可能无解。
\(2\le n\le 10^5\),\(0\le a_i<2^{30}\)。
令 \(a_0=\bigoplus\limits_{i=1}^n a_i\),操作 \(x\) 相当于交换 \(a_0,a_x\)。
于是判有无解就是 \(\{b_{1\dots n}\}\subseteq\{a_{0\dots n}\}\)。
建图,\(a_i\to b_i(a_i\ne b_i)\),每个连通块必有欧拉回路,长 \(len\) 的欧拉回路 \(len+1\) 步必定可以归位。
于是答案即为 \(\small\mathbf{边数+连通块数}\)。
如果 \(s\) 是孤立点,则不用 \(s\),答案 \(-1\)。
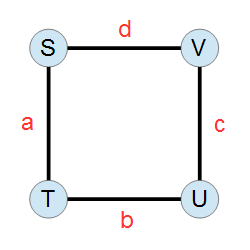
[AGC051D] C4
有一张四个点的无向图:
这四条边分别是 \(a,b,c,d\) 条重边。
求欧拉回路数量。
\(a,b,c,d\le 5\times 10^5\)。
直接枚举,强制定向,BEST 定理,答案为:
复杂度 \(O(a)\)。
[AGC031F] Walk on Graph
有 \(n\) 点 \(m\) 边的带边权无向图,\(q\) 次询问 \(u,v,L\):
是否存在 \(u\to v\) 的路径,经过边 \(e_{0\sim k}\),使得 \(\sum\limits_{i=0}^k w_{e_i}\equiv L\pmod p\),其中 \(w_e\) 是 \(e\) 的边权。
\(p\) 是给定的模数,保证 \(p\) 为奇数。
\(1\le n,m\le 5\times 10^4\),\(3\le p\le 10^6\)。
这个 \(\sum\limits_{i=0}^k w_{e_i}\) 很难搞,考虑倒推 \(v\to u\):
\(x\) 初始为 \(0\),走过一条边权 \(w\) 的边,则 \(x\gets (2x+w)\bmod p\),需要最终使 \(x=L\)。
状态为 \((u,x)\),边 \(u\overset{w}{\rightarrow}v\) 则 \((u,x)\to(v,2x+w)\)。(对 \(p\) 取模接下来都省略)
性质 \(1\):\((u,x)\to(v,y)\) 则 \((v,y)\to (u,x)\)。
\(p\) 为奇数,\(\gcd(2,p)=1\),\(2^{\varphi(p)}\equiv 1\pmod p\)。
取 \(t=2\varphi(p)\),一条边反复走 \(t\) 次则状态不变。同样地,一条路径走 \(t\) 次状态不变。
若有路径 \((u,x)\to(v,y)\),则 \((u,x)\) 走 \(t\) 次这条路径还会回到 \((u,x)\)。
换言之,则 \((v,y)\) 走 \(t-1\) 次这条路径到 \((u,x)\)。
性质 \(2\):若图中有边权为 \(a,b\) 的两条边,对于任意 \(u,x\) 有 \((u,x)\leftrightarrow(u,4x+3(a-b))\)。
\((u,x)\) 走两遍一条边权 \(w\) 的边可到 \((u,4x+3w)\),\((u,x)\leftrightarrow(u,4x+3w)\)。
有两条连向 \(u\) 的边,边权为 \(a,b\),则对于任意 \(x\) 有 \((u,x)\leftrightarrow(u,x+3(a-b))\)。
证明:\((u,4y+3a)\leftrightarrow(u,y)\leftrightarrow(u,4y+3a)\),换元 \(x=4y+3b\) 即可。
有两条连向 \(v\) 的边,边权为 \(a,b\),则对于任意 \(u,x\) 有 \((u,x)\leftrightarrow(u,x+3(a-b))\)。
证明:\((u,x)\leftrightarrow(v,y)\leftrightarrow(v,y+3(a-b))\leftrightarrow(u,x+3(a-b))\)。
若存在 \(?\overset{a}{\leftrightarrow}u\overset{b}{\leftrightarrow}v\overset{c}{\leftrightarrow}?\),则有 \((u,x)\leftrightarrow(u,x+3(a-c))\)。
证明:\((u,x)\leftrightarrow(u,x+3(a-b))\leftrightarrow(u,x+3(a-b)+3(b-c))\)。
结合这三点即可推出性质 \(2\)。
裴蜀定理,\(g'=\gcd\limits_{a,b\in E}w_a-w_b\),\(g=\gcd(g',p)\),则对于任意 \(u,x\) 有 \((u,x)\leftrightarrow(u,x+3g)\)。
注意到 \(\forall a,b\in E,g|w_a-w_b\),所有边权模 \(g\) 同余,余数为 \(r\),则边权可以表示成 \(kg+r\) 的形式。
给所有边权减去 \(r\),把所有状态的第二维加上偏移量 \(r\),这样边权都是 \(g\) 的倍数了。
第二维对 \(3g\) 取模,状态 \((u,x)\) 能到达的状态均形如 \((v,2^dx+kg)\),\(k\in\{0,1,2\}\)。
又有 \((u,x)\to(u,4x+kg)=(u,2^2x+kg)\),则 \(d\in\{0,1\}\),这样第二维只有 \(6\) 种可能了。
并查集维护,时间复杂度 \(O((n+q)\alpha(n)+p)\)。
[AGC008E] Next or Nextnext
给长度为 \(n\) 的序列 \(a\),求有多少 \(1\sim n\) 的排列 \(p\) 满足:
\(\forall i\in[1,n],a_i=p_i\ \operatorname{or}\ a_i=p_{p_i}\)。
答案对 \(10^9+7\) 取模。
\(1\le n\le 10^5\),\(1\le a_i\le n\)。
提示:这些图的来源为AtCoder 官方题解。
考虑判定 \(p\),建出 \(i\to p_i\) 的图 \(G_p\),\(i\to a_i\) 在环上距离 \(\le 2\)。
现在有 \(i\to a_i\) 的图 \(G_a\),考虑如何合并出 \(i\to p_i\) 的图。
\(G_a\) 是内向基环树森林,先不考虑基环树,考虑环的情况:
- 环上所有点 \(a_i=p_i\)。
- 环上所有点 \(a_i=p_{p_i}\),需要 \(n>1\) 且 \(n\) 为奇数。(\(n=1\) 时与 1. 重复)
- 发现 \(G_p\) 偶环所有点 \(a_i=p_{p_i}\) 会拆成两半,\(G_a\) 的两个大小相同的环可以合并,方案数是环长。

每种环长分别计算,当前环长是 \(m\),进行一个 DP,\(f_i\) 表示 \(i\) 个环的方案数:
定义 \(c\) 为 \(1+[m>1\ \operatorname{and}\ m\equiv 1\pmod 2]\),即 1. 和 2. 情况的方案数。转移:
\(\rule{20cm}{0.05em}\\\)
接下来考虑基环树,基环树不能和环合并,所以贡献与环独立。

基环树除去环一定是若干条链,否则无解。

设 \(l1\) 为当前链长,\(l2\) 为上一个条链的根和这条链的跟的环上距离。
- \(l1<l2\),\(2\) 种方案。
- \(l1=l2\),\(1\) 种方案。
- \(l1>l2\),\(0\) 种方案。
时间复杂度 \(O(n)\)。
数论
CF338D GCD Table
给 \(n,m\) 和长为 \(k\) 的序列 \(a\)。
求是否存在 \(i\in[1,n],j\in[1,m-k+1]\) 使得 \(\forall x\in[1,k],\gcd(i,j+x-1)=a_x\)。
\(1\le n,m,a_i\le 10^{12}\),\(1\le k\le 10^4\)。
若有解,\(i=\operatorname{lcm}\limits_{x=1}^k a_x\) 必定有解。
确定 \(i\) 后有 \(j\equiv 1-x\pmod{a_x}\),EXCRT 即可。
这样算出来的 \(j\) 只满足 \(\forall x\in[1,k],a_x|\gcd(i,j+x-1)\),带入检验 \(a_x=\gcd(i,j+x-1)\)。
51Nod 1190 最小公倍数之和 V2
\(T\) 组数据,给 \(n,m\),求:
\[\sum_{i=n}^m\operatorname{lcm}(i,m) \]对 \(10^9+7\) 取模。
\(1\le T\le 5\times 10^3\),\(1\le n\le m\le 10^9\)。
枚举 \(p\),\(r\) 每个质因子指数只能是 \(0/1\),\(O(2^{\omega(m)}\omega(m))\) 子集卷积。
单组数据时间复杂度 \(O(d(m)+2^{\omega(m)}\omega(m))\)。
但是我懒得写子集卷积,直接 \(O(d(m)+3^{\omega(m)})\)。
51Nod 1227 平均最小公倍数
给 \(n,m\),定义:
\[F(x)=\frac{1}{x}\sum_{i=1}^x\operatorname{lcm}(i,x) \]求:
\[\sum_{i=n}^m F(i) \]对 \(10^9+7\) 取模。
\(1\le n\le m\le 10^{10}\)。
\(n\) 以内与 \(n\) 互质的数的和有一个式子:
整除分块 \(d\),现在问题来到求解 \(\dfrac{n\cdot\varphi(n)+\varepsilon(n)}{2}\) 的前缀和。
实际上只需要求解 \(f(n)=n\cdot\varphi(n)\) 的前缀和。
杜教筛,构造:
时间复杂度 \(O(n^{\frac{2}{3}})\)。
GDOI2016day3 互补约数
定义:
\[f(n)=\sum_{d|n}\gcd(d,\frac{n}{d}) \]给 \(n\),求:
\[\sum_{i=1}^n f(i) \]\(n\le 10^{12}\)。
有
所以
则
暴力枚举 \(d\),对 \(i\) 整除分块。
时间复杂度:
CometOJ 1098 神奇函数
定义 \(d(x)\) 为 \(x\) 的最小质因子。
多组数据,给 \(n\),求 \(\displaystyle \sum_{i=1}^n f(i)\)。
\(1\le T\le 10\),\(1\le n\le 10^{13}\)。
分解 \(\displaystyle x=\prod_{i=1}^c p_i^{k_i}\)。
最后一步是:\(j\) 的质因子 \(p_i^{k'_i}\),要求 \(k'_i\ge\lceil{\frac{k_i}{2}}\rceil\),则 \(2k'_i\ge k_i\)。
定义 \(P(x)\) 表示 \(x\) 是否为完全平方数,即 \(P(x)=\exists i\in \mathbb{Z},x=i^2\)。
整除分块扩展:\(\lfloor{\dfrac{n}{i^2}}\rfloor\) 一共 \(n^{\frac{1}{3}}\) 段。
于是可以做到 \(O(\sqrt n+Tn^{\frac{1}{3}})\)。
51Nod 1847 奇怪的数学题
定义 \(\operatorname{sgcd}(i,j)\) 为 \(i,j\) 的第二大公约数,特别地,\(\gcd(i,j)=1\) 则 \(\operatorname{sgcd}(i,j)=0\)。
给定 \(n,k\),求:
\[\sum_{i=1}^n\sum_{j=1}^n \operatorname{sgcd}(i,j)^k \]\(1\le n\le 10^9\),\(1\le k\le 50\)。
定义 \(minp(x)\) 为 \(x\) 的最小质因子。
若 \(t=\gcd(i,j)>1\),则 \(\operatorname{sgcd}(i,j)=\dfrac{t}{minp(t)}\)。


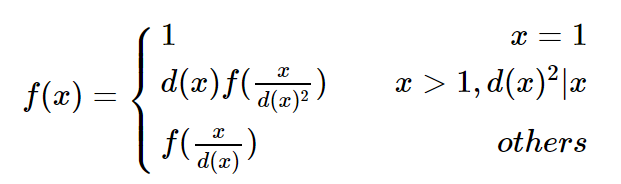

 浙公网安备 33010602011771号
浙公网安备 33010602011771号