[2021-Fall] Lab04 of cs61A of UCB

Intro

---

我发现解决递归的问题真的很有意思, 我喜欢这种解决问题的方式, 代码足够简洁而且做出来很直观, 这也是我写下这篇文章的原因.

📒 如何解决好递归的问题 ?

1. 想清楚什么是 base case ?
2. 怎么把当前的问题分解为更简单的问题 ? 时刻要记住我们定义的函数的定义

后面我也会按照这个思路来解决这个 lab 中的递归问题

Recursion

---

Q2: Summation

Write a recursive implementation of summation, which takes a positive integer n and a function term. It applies term to every number from 1 to n including n and returns the sum.

Important: Use recursion; the tests will fail if you use any loops (for, while).

1. 什么是这一题的 base case ? 这个很容易想到, 因为我们要处理从 1 到 n, 显然当 n = 1 的时候就是我们的 base case, 此时返回 term(n)

2. 怎么把当前的问题分解为更简单的问题 ? 因为是从 1 到 n, 我们每次让 n - 1 来缩小问题的规模, 就会一直到达 base case

def summation(n, term):
    """Return the sum of numbers 1 through n (including n) wíth term applied to each number.
    Implement using recursion!

    >>> summation(5, lambda x: x * x * x) # 1^3 + 2^3 + 3^3 + 4^3 + 5^3
    225
    >>> summation(9, lambda x: x + 1) # 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
    54
    >>> summation(5, lambda x: 2**x) # 2^1 + 2^2 + 2^3 + 2^4 + 2^5
    62
    >>> # Do not use while/for loops!
    >>> from construct_check import check
    >>> # ban iteration
    >>> check(HW_SOURCE_FILE, 'summation',
    ...       ['While', 'For'])
    True
    """
    assert n >= 1
    # base case: n = 1
    if n == 1:
        return term(n)
    else:
        return term(n) + summation(n - 1, term)

Tree Recursion

---

Q3: Pascal's Triangle

Here's a part of the Pascal's trangle:

1
1 1
1 2 1
1 3 3 1
1 4 6 4 1

Every number in Pascal's triangle is defined as the sum of the item above it and the item above and to the left of it. Use 0 if the item does not exist.

Define the procedure pascal(row, column) which takes a row and a column, and finds the value of the item at that position in Pascal's triangle. Rows and columns are zero-indexed; that is, the first row is row 0 instead of 1 and the first column is column 0 instead of column 1.

For example, the item at row 2, column 1 in Pascal's triangle is 2.

这个问题是很经典的帕斯卡三角形问题了, 根据定义我们可以知道在 Pascal(i, j) 这个位置, 要得到它的值我们可以用 Pascal(i - 1, j) + Pascal(i - 1, j - 1) 来计算, 显然这个定义式天然给出了递归分解子问题的方式. 那么我们剩下要解决的就是「什么是 base case ?」, 显然只要是在第一列(j = 0)或者说行号和列号(i == j)相等, 那么就是 1. 再看看上面的帕斯卡三角形示例, 你会发现这两个 base case + 递归分解子问题的方式我们就可以计算出所有的情况.

注意我们还要考虑到索引非法的情况(j > i)

def pascal(row, column):
    """returns the value of the item in pascal's triangle 
    whose position is specified by row and column.
    >>> pascal(0, 0)
    1
    >>> pascal(0, 5)	# empty entry; outside of pascal's triangle
    0
    >>> pascal(3, 2)	# row 3 (1 3 3 1), column 2
    3
    >>> pascal(4, 2)     # row 4 (1 4 6 4 1), column 2
    6
    """
    # in pascal's triangle, \
    # pascal(i, j) = pascal(i - 1, j - 1) + pascal(i - 1, j)

    # base case 1. empty entry
    if column > row:
        return 0
    # base case 2. pascal(i, 0)
    if column == 0:
        return 1
    # base case 3. pascal(i, i)
    elif row == column:
        return 1
    return pascal(row - 1, column) + pascal(row - 1, column - 1)

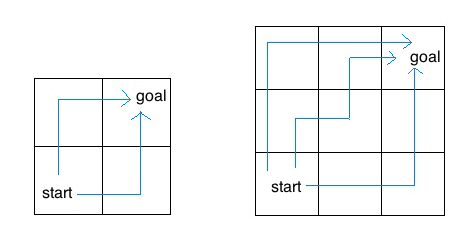
Q4: Insect Combinatorics

Consider an insect in an M by N grid. The insect starts at the bottom left corner, (0, 0), and wants to end up at the top right corner, (M-1, N-1). The insect is only capable of moving right or up. Write a function paths that takes a grid length and width and returns the number of different paths the insect can take from the start to the goal. (There is a closed-form solution to this problem, but try to answer it procedurally using recursion.)

For example, the 2 by 2 grid has a total of two ways for the insect to move from the start to the goal. For the 3 by 3 grid, the insect has 6 diferent paths (only 3 are shown above).

Hint: What happens if we hit the top or rightmost edge?

从题目中我们可以知道我们只能向上走或者向右走, 也就是说假设我们处在 path(i, j) 这个位置, 那么我们只可能是从左边或者是从下边来的, 那么走到 path(i, j) 有几种走法呢 ? 显然, 它等于 path(i, j - 1) + path(i - 1, j). (这里左下角才是 (0, 0)). 那么我们剩下要解决的就是「什么是 base case ?」, 也就是一直往上走和一直往右走这两种, 都只有 1 中走法. 如下面这个表格所示:

1
1
1	1	1

再根据上面的公式可以知道, 完整的应该是这样:

1	3	6
1	2	3
1	1	1

这里为了处理问题方便, 我们让索引从 1 开始

List Comprehensions

---

Q5: Couple

Implement the function couple, which takes in two lists and returns a list that contains lists with i-th elements of two sequences coupled together. You can assume the lengths of two sequences are the same. Try using a list comprehension.

Hint: You may find the built in range function helpful.

这个问题简单, 因为两个是等长的 list, 所以我们只要用同一个索引从两个 list 中取数即可

def couple(s, t):
    """Return a list of two-element lists in which the i-th element is [s[i], t[i]].

    >>> a = [1, 2, 3]
    >>> b = [4, 5, 6]
    >>> couple(a, b)
    [[1, 4], [2, 5], [3, 6]]
    >>> c = ['c', 6]
    >>> d = ['s', '1']
    >>> couple(c, d)
    [['c', 's'], [6, '1']]
    """
    assert len(s) == len(t)
    return [[s[i], t[i]] for i in range(len(s))]

Q6: Coordinates

Implement a function coords that takes a function fn, a sequence seq, and a lower and upper bound on the output of the function. coords then returns a list of coordinate pairs (lists) such that:

• Each (x, y) pair is represented as [x, fn(x)]
• The x-coordinates are elements in the sequence
• The result contains only pairs whose y-coordinate is within the upper and lower bounds (inclusive)

See the doctest for examples.

Note: your answer can only be one line long. You should make use of list comprehensions!

这个其实也容易, 就是多了一个 if 语句来过滤掉不符合条件的结果而已

def coords(fn, seq, lower, upper):
    """
    >>> seq = [-4, -2, 0, 1, 3]
    >>> fn = lambda x: x**2
    >>> coords(fn, seq, 1, 9)
    [[-2, 4], [1, 1], [3, 9]]
    """
    "*** YOUR CODE HERE ***"
    return [[i, fn(i)] for i in seq if lower <= fn(i) <= upper]

Q7: Riffle Shuffle

A common way of shuffling cards is known as the riffle shuffle. The shuffle produces a new configuration of cards in which the top card is followed by the middle card, then by the second card, then the card after the middle, and so forth.

Write a list comprehension that riffle shuffles a sequence of items. You can assume the sequence contains an even number of items.

Hint: There are two ways you can write this as a single list comprension: 1) You may find the expression k%2, which evaluates to 0 on even numbers and 1 on odd numbers, to be alternatively access the beginning and middle of the deck. 2) You can utilize an if expression in your comprehension for the odd and even numbers respectively.

这一个问题会稍微难一点, 我们其实是要想办法得到正确的索引, 显然索引为奇数和偶数的时候情况并不相同. 我们可以看如下的表格找一下规律⬇️:

Origin index	0	1	2	3
Real index for deck[...]	0	2	1	3
Guess ? (M = 2)	0	M	2 // 2 ?	M + 1 = M + 3 // 2 ?

• 奇数: 0, 1, 2, ...
• 偶数: M+0, M+1, M+2, ...

通过上面的观察我们就可以写出如下的代码⬇️:

def riffle(deck):
    """Produces a single, perfect riffle shuffle of DECK, consisting of
    DECK[0], DECK[M], DECK[1], DECK[M+1], ... where M is position of the
    second half of the deck.  Assume that len(DECK) is even.
    >>> riffle([3, 4, 5, 6])
    [3, 5, 4, 6]
    >>> riffle(range(20))
    [0, 10, 1, 11, 2, 12, 3, 13, 4, 14, 5, 15, 6, 16, 7, 17, 8, 18, 9, 19]
    """
    return [deck[i // 2 + (i % 2) * (len(deck) // 2)] for i in range(len(deck))]