How Do Recommendation Models Amplify Popularity Bias? An Analysis from the Spectral Perspective
概
本文分析在不引入额外的约束下, 基于矩阵分解的模型倾向于匹配 item 的流行度.
符号说明
- \(\mathcal{U}\), user set, \(|\mathcal{U}| = n\);
- \(\mathcal{I}\), item set, \(|\mathcal{I}| = m\);
- \(Y \in \{0, 1\}^{n \times m}\), interaction matrix;
- \(r_i = \sum_{u \in \mathcal{U}} y_{ui}\), 表示 item 的交互频率, 总的构成流行度向量 (popularity vector) \(\mathbf{r}\).
Popularity bias
-
我们考虑基于矩阵分解的方法, 它提供:
\[\mathbf{u}_u, \mathbf{v}_i, \]用以计算 user \(u\) 和 item \(i\) 之间的相似度
\[\hat{y}_{ui} = \mu (\mathbf{u}_u^T \mathbf{v}_i), \]这里 \(\mu(\cdot)\) 表示激活函数.
-
令 \(\mathbf{U} \in \mathbb{R}^{n \times d}, \mathbf{V} \in \mathbb{R}^{m \times d}\) 表示 user, item 的向量矩阵, 可得
\[\hat{\mathbf{Y}} = \mu (\mathbf{U} \mathbf{V}^T). \] -
对预估的得分矩阵 \(\hat{\mathbf{Y}}\) 进行 SVD 分解:
\[\tag{1} \hat{\mathbf{Y}} = \mathbf{P\Sigma Q^T} = \sum_{1 \le k \le L} \sigma_k \mathbf{p}_k \mathbf{q}_k^T, \quad L= \min(n, m), \]且 \(\sigma_1 \ge \sigma_2 \ge \ldots \ge \sigma_L\).
\(\mathbf{q}_1\) 和 \(\mathbf{r}\) 具有高相似度

-
上图展示了 (1) 中的主(右)奇异向量 \(\mathbf{q}_1\) 和 popularity vector \(\mathbf{r}\) 的 cosine 相似度:
\[\frac{\mathbf{q}_1^T \mathbf{r}}{\|\mathbf{q}_1\| \cdot \|\mathbf{r}\|} \]非常接近 1. 因此, 我们可以认为, 传统模型所学到的得分矩阵 \(\hat{\mathbf{Y}}\) 其实受到了非常非常多的流行度的影响.
-
进一步地, 我们可以理论证明这一点:
-
Theoerm 1 (Popularity memorization effect): 给定一个 embedding-based 的模型且具备足够的表达能力, 当 \(\mathbf{r}\) 服从 power-law, 我们有:
\[\cos (\mathbf{q}_1, \mathbf{r}) \ge \frac{\sigma_1^2}{r_{\max} \sqrt{\zeta (2 \alpha)}} \sqrt{ 1 - \frac{r_{\max} (\zeta (\alpha) - 1)} {\sigma_1^2} }, \]其中 \(r_{\max} = \max_i r_i\), \(\zeta (\alpha)\) 表示 Riemann zeta function \(\zeta (\alpha) = \sum_{j=1}^{\infty} \frac{1}{j^{\alpha}}\).
proof:
-
注意, 这里假设模型有足够的表达能力, 即假设 \(\hat{\mathbf{Y}}\) 能够足够近似 \(\mathbf{Y}\), 于是后面的分析相当于都是基于 \(\mathbf{Y}\) 的 SVD 分解之上.
-
于是
\[\cos(\mathbf{q}_1, \mathbf{r}) =\frac{\mathbf{q}_1^T \mathbf{r}}{\|\mathbf{r}\|} =\frac{\mathbf{q}_1^T \mathbf{Y}^T \mathbf{e}}{\|\mathbf{r}\|} =\frac{\sigma_1 \mathbf{p}_1^T \mathbf{e}}{\|\mathbf{r}\|}. \] -
又
\[\| \mathbf{r} \| = \sqrt{\sum_{i=1}^m r_i^2} =\sqrt{\sum_{i=1}^m (r_{\max} \cdot i^{-\alpha})^2} =r_{\max} \sqrt{\sum_{i=1}^m i^{-2\alpha}} \le r_{\max} \sqrt{\zeta (2 \alpha)}. \] -
于是
\[\cos (\mathbf{q}_1, \mathbf{r}) \ge \frac{ \sigma_1 \mathbf{e}^T \mathbf{p}_1 }{ \mathbf{r}_{\max} \sqrt{\zeta (2 \alpha)} }. \] -
后续需要 bound \(\sigma_1\) 和 \(\mathbf{e}^T \mathbf{p}_1\), 需要更多的符号引入 (详情请回看原文).
相似度随着维度降低而增加
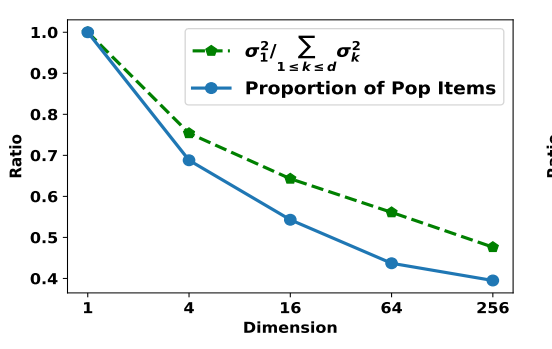
- 这个其实是比较显然, 因为维度降低总的能量降低了.
相似度随着训练的变化
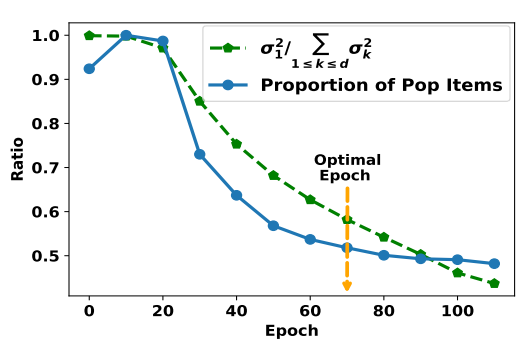
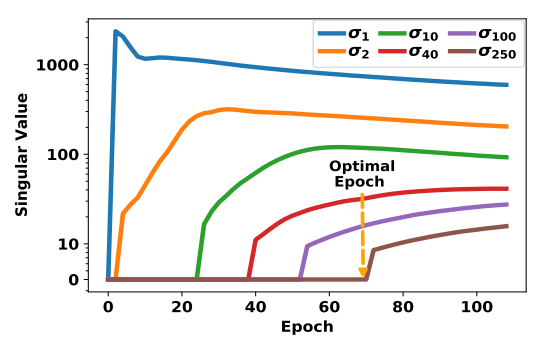
- 随着训练进行, popularity bias 的影响是逐步降低的, 但是过低实际上会导致效果的下降, 这似乎说明了 popularity bias 的需要维持在一定程度, 过低或这过高都不太好.
ReSN: Regulartion with Spectral Norm
-
本文提出的方法是:
\[\mathcal{L}_{\text{ReSN}} = \mathcal{L}_R (\mathbf{Y}, \hat{\mathbf{Y}}) + \beta \|\hat{\mathbf{Y}}\|_2^2, \]这里 \(\|\cdot \|^2\) 是谱范数.
-
但是这个计算是复杂的, 因此用如下的替代
\[\frac{ \beta }{ \| \mathbf{VU}^T \mathbf{e} \|^2 } \| \mathbf{UV^TVU}^T \mathbf{e} \|^2. \]相当于, 我们要求最后得到 score matrix 和流行度向量
\[\mathbf{V}\mathbf{U}^T \mathbf{e} \]的匹配度不能太高 (根据证明, \(\mathbf{V}\mathbf{U}^T \mathbf{e}\) 是比较接近 \(\mathbf{q}_1\) 的).


 浙公网安备 33010602011771号
浙公网安备 33010602011771号