Convergence of Adam Under Relaxed Assumptions

目录

• 概
• 符号说明
• 思路

Li H., Jadbabaie A. and Rakhlin A. Convergence of adam under relaxed assumptions. NeurIPS, 2023.

概

本文探讨了 Adam 再较弱的假设下的收敛性. 作者的证明思路非常有趣, 虽然条件看着还是有些不对劲.

符号说明

• $f(x)$, 非凸目标函数;
• $f(x, \xi)$, $\xi$ 是一些随机 source, 可用于模拟训练过程中的随机因素 (如 mini-batch sampling);

• 上述算法是 Adam 的完整流程, 需要注意的是, 这里的 $\beta$ 在常规的实现中为 $1 - \beta$.

思路

• 作者的证明思路是围绕:

  $$\tag{1} f(x_{t+1}) - f(x_t) \mathop{\le}\limits^{how?} -\frac{\eta}{4G} \|\nabla f(x_t)\|^2 + \frac{\eta}{\lambda} \|\epsilon_t\|^2,$$

  其中

  $$\epsilon_t = \hat{m}_t - \nabla f(x_t).$$

• 倘若我们能够假设 $f$ 是 $L$-smooth 的, (1) 是可以容易证明的. 但是作者搞了一个 ($L_0$, $L_p$)-smooth 这个局部 smooth 的条件 (更弱一点). 从而需要证明在这个条件下有着类似 $L$-smooth 的性质, 文中 Section 5 和 Appendix B 都在讨论这一点.

• 有趣的是, 作者先假设 $t \le \tau$ 下所需性质成立, 然后再证明 $\tau = T + 1$ (通过反证法).

• 有了 (1), 剩下的难点在于如何 bound 住 $\|\epsilon_t\|$, 更准确地说, 是如何次线性地 bound 住:

  $$\sum_{t=1}^T \|\epsilon_t\|^2.$$

  我们需要注意, 这里的难点在于:

  1. $\hat{m}_t$ 是通过 $f(x_t, \xi_t)$ 随机梯度得到的;
  2. 就是本身的误差积累如何能够保证次线性.

• 作者用概率上的方法 (Azuma-Hoeffding inequality) 证明了:
  

• 请注意我标黄的地方:

  1. 这是个概率上成立的结果;
  2. $\beta T$ 不看 $\beta$ 是线性增长的, 想要规避这一点需要保证 $\beta$ 是一个很小的量. 事实上作者也这么做了.

• 下面是主要的结果:

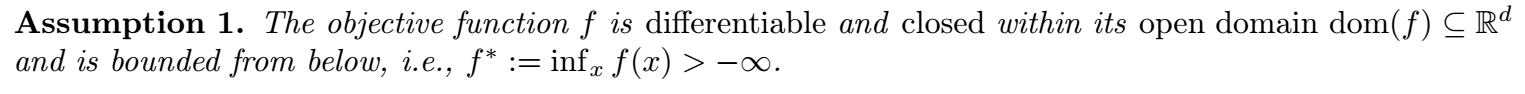
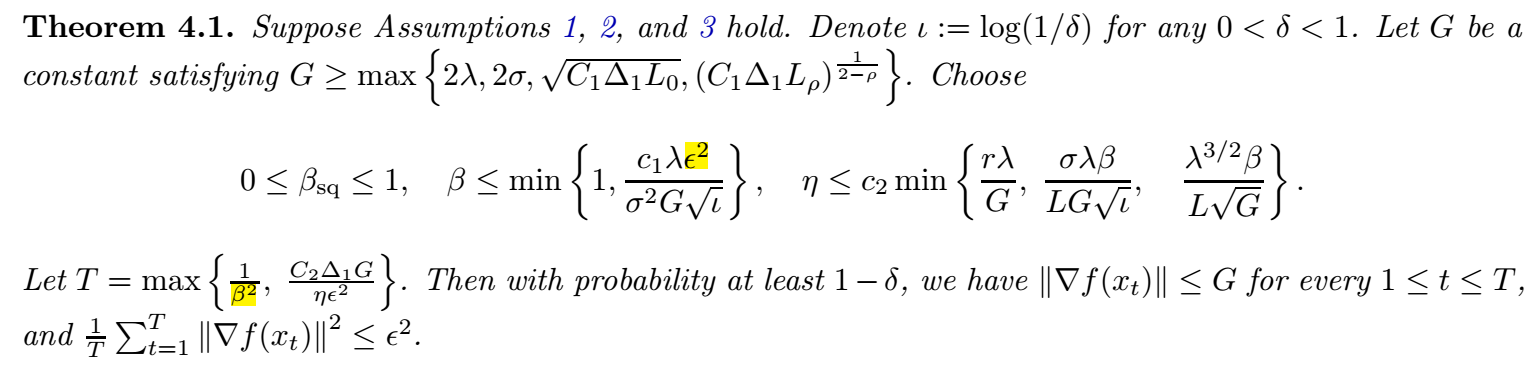
• 感觉美中不足的点就是 $\beta$ 的选择, 一定是一个非常非常小的值, 而且这个 $\beta$ 取得小和常规的不一样, 是更倾向于平均的结果, 即相当于一般情况取个 $0.999999$ 的感觉, 这个太不符合实际了. 而且 $T$ 的这种取法也不妥当, 有点掩盖了真实的收敛速度.